2. Спеціальні види простих графів

У теорії графів виділяють деякі спеціальні види, що застосовуються під час розв’язування багатьох задач.

Означення 2.1. Граф називається однорідним (або регулярним), якщо степені всіх його вершин рівні.

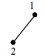
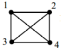
Приклад однорідних графів зображено на рис 2.1.

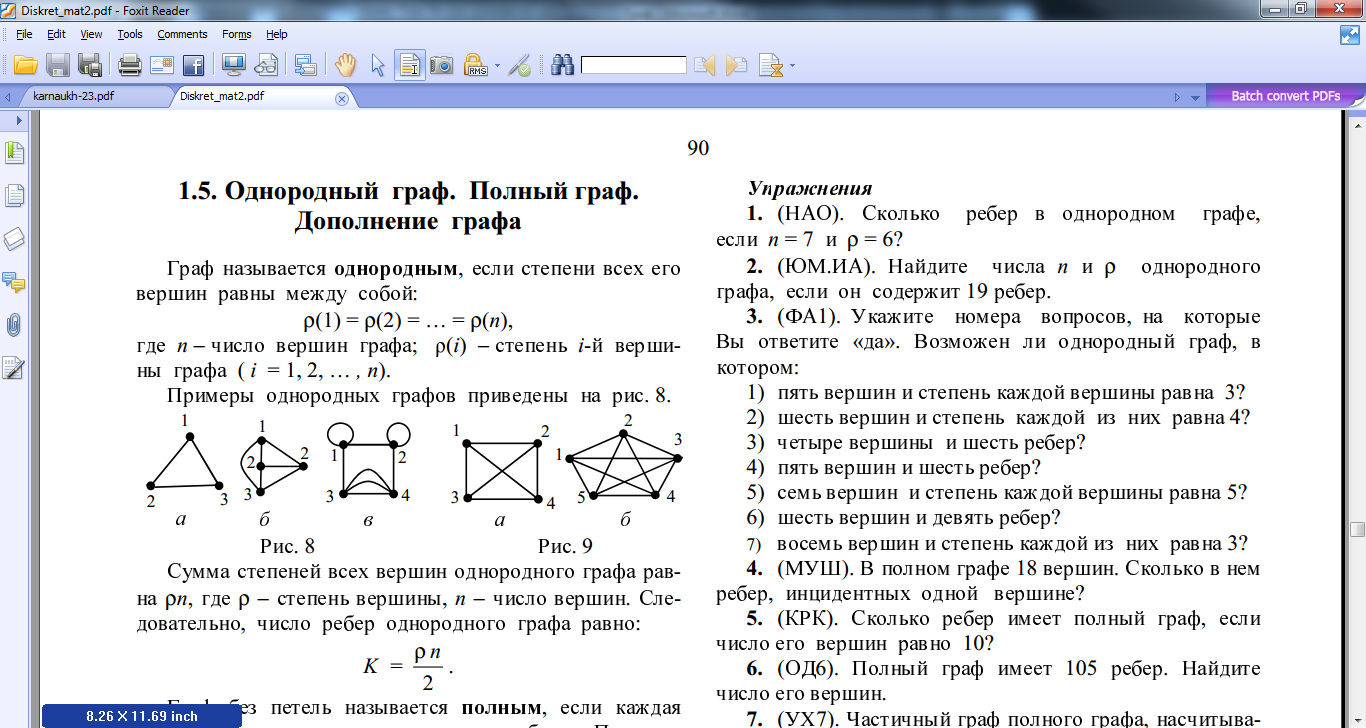
Рис. 2.1. Однорідні графи

Сума степенів усіх вершин однорідного графу дорівнює deg(v)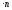, деn– кількість вершин графа. Відповідно кількість ребер однорідного графу рівна.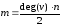

Означення 2.2. Простий граф називається повним, якщо всі його вершини з’єднані між собою точно одним ребром.

Повні графи позначаються K_n, деn– кількість вершин. Приклад повних графів наведено на рис 2.2.

а)	б)	в)

Рис. 2.2. Повні графи а) К₁; б)К₂; в)К₃

Кількість ребер у графі K_n рівна.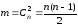

Приклад 2.1.У повному графі 6 вершин. Скільки у ньому ребер?

Відповідь..

Означення 2.2. Простий граф називається дводольним, якщо множину його вершинVможна розбити на дві підмножини (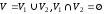), що не перетинаються таким чином, що кожне ребро з’єднує вершину зV₁таV₂.

Означення 2.3. Дводольний граф називається повним, якщо кожна вершина зV₁з’єднана з усіма вершинамиV₂.

Повний дводольний граф позначають K_k,p, де.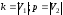

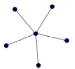
Зауважимо, що граф K_1,pназивається зіркою.

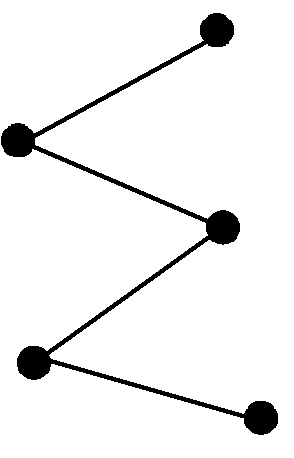
Приклад дводольних графів наведено на рис 2.3.

а)	б)	в)

Рис. 2.3. Дводольні графи а) неповний дводольний граф; б) зірка К_1,5; в) повний дводольний графК_2,3

Кількість ребер у графі K_k,p рівна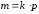, а кількість вершинn =k+p.

Приклад 2.2.ЗаданоK_2,4. Скільки у даному графі ребер та вершин?

Відповідь.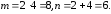Отже, 8 ребер та 6 вершин.

Використовуючи поняття повного графу можна по-іншому сформулювати означення 1.9 про доповнення до графу.

Означення 2.3. Граф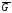є доповненням до графуG, якщо їхнє об’єднання утворює повний граф, тобто, а перетин множин ребер графів Gта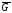утворює пусту множину.

Кількість ребер у доповнювальному графі 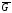рівна, деn – кількість вершин графаG,а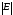– кількість ребер графаG.Кількість вершин доповнювального графу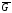дорівнює кількості вершин графуG.

Приклад 2.3.ГрафG містить 5 вершин та 8 ребер. Скільки вершин та ребер в доповнювальному графі?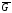

Відповідь.Кількість вершин графу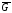 дорівнює кількості вершин графуG, тобтоn= 5.

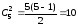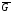Для того, щоб обчислити кількість ребер у доповнювальному графі необхідно знайти кількість ребер у повному . Отже, кількість ребер у доповнювальному графірівна.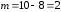

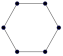
Означення 2.4. Простий граф називається циклом (n≥3), якщо всі його вершини з’єднані у замкнуте кільце.

Графи-цикли позначаються С_n, деn– кількість вершин. Приклад циклів наведено на рис 2.3.

а)	б)	в)

Рис. 2.3. Графи-цикли а) С₃; б)С₄; в)C₆

Кількість ребер у графі C_n рівна

Приклад 2.3.Задано графC₅. Скільки вершин та ребер в доповнювальному графі?

Відповідь.Кількість вершин графу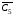 дорівнює кількості вершин графуC₅, тобтоn= 5.

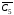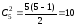Для того, щоб обчислити кількість ребер у потрібно знайти кількість ребер у повному, кількість ребер у графіC₅відповідно дорівнює 5. Отже, кількість ребер у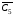дорівнює.

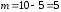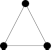
Означення 2.4. Простий граф називається колесом (n≥3), якщо він отриманий з’єднанням однієї єдиної вершини з усіма вершинами графуC_n.

Граф-колесо позначається W_n, деn– кількість вершин у графі цикліC_n. Приклад таких графів наведено на рис 2.4.

а)	б)	в)

Рис. 2.4. Графи-колесо а) W₃; б)W₄; в)W₆

Кількість ребер у графі W_n рівна, а кількість вершин дорівнюєn+1.

Приклад 2.4.Задано графW₅. Скільки вершин та ребер в доповнювальному графі?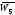

Відповідь.Кількість вершин графу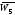 дорівнює кількості вершин графуC₅, тобтоn= 6.

Для того, щоб обчислити кількість ребер у 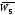потрібно знайти кількість ребер у повному, кількість ребер у графіW₅відповідно дорівнює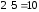. Отже, кількість ребер у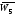дорівнює.

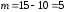Приклад 2.5.У графі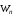20 ребер. Скільки вершин у даному графі?

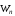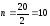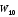Відповідь.Кількість вершин графудорівнюєn+1. Так як, то кількість вершин графу= 11.

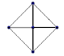
Означення 2.5. Простий граф називаєтьсяn-мірним кубом, якщо він зображає усі бітові рядки довжиною 2ⁿ.

n-мірний куб позначаєтьсяQ_n. Зауважимо, що дві вершини в графіQ_nз’єднані ребром тоді, коли бітові рядки, які вони зображують, не відрізняються більше, ніж на біт. Приклад таких графів наведено на рис 2.5.

а)	б)	в)

Рис. 2.5. n-мірні куби а)Q₁; б)Q₂; в)Q₃