- •Вступ до теорії графів методичні вказівки
- •6. 050103 „Програмна інженерія”
- •Теоретичні відомості Вступ
- •Основні означення теорії графів
- •Спеціальні види простих графів
- •Представлення графів
- •Ізоморфізм графів
- •Планарні та плоскі графи
- •Завдання до виконання
- •Контрольні запитання.
- •Список літератури
- •Вступ до теорії графів методичні вказівки
Ізоморфізм графів
Буквальний переклад слова “ізоморфізм” означає “однаковість форми”. Форма графа — це його структура. Таким чином, ізоморфізм графів означає однаковість їх структури.
Означення 4.1.Два графиG1= (V1, E1) іG2= (V2,E2) називаються ізоморфними (це позначаєтьсяG1≅G2), якщо між множинами їх вершин існує взаємно однозначне відображенняϕ:V1→V2, яке зберігає суміжність, тобто для довільних вершинvіw(v,w)∈E1тоді й тільки тоді, коли (ϕ(v),ϕ(w))∈E2. При цьомуϕназивається ізоморфним відображенням або ізоморфізмом графаG1на графG2.
Тобто графи і
і ізоморфні,якщо їхні вершини можна
пронумерувати таким
чином: у графі
ізоморфні,якщо їхні вершини можна
пронумерувати таким
чином: у графі позначаємо вершини (v1,v2,…,vn),
у графі
позначаємо вершини (v1,v2,…,vn),
у графі позначаємо вершини (w1,w2,….wn),
що довільні дві вершини (vі,vj)
графуG1суміжні
тоді і тільки тоді, коли суміжні відповідні
вершини (wi,wj)
у графі
позначаємо вершини (w1,w2,….wn),
що довільні дві вершини (vі,vj)
графуG1суміжні
тоді і тільки тоді, коли суміжні відповідні
вершини (wi,wj)
у графі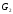 .
.
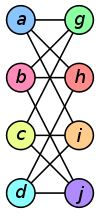
Два графи показані нижче в табл. 4.1 ізоморфні, незважаючи на свою зовнішню відмінність.
Таблиця 4.1
|
Граф G |
Граф H |
Ізоморфізм між G і H |
|
|
|
ƒ(a) = 1 ƒ(b) = 6 ƒ(c) = 8 ƒ(d) = 3 ƒ(g) = 5 ƒ(h) = 2 ƒ(i) = 4 ƒ(j) = 7 |
Приклад 4.1.Графи, зображені на рис. 4.1(а), (б) – ізоморфні.
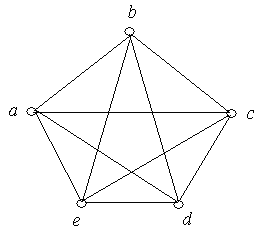
(а) (б)
Рис. 4.1. Приклади ізоморфних графів.
Необхідні умови. Алгоритм перевірки графів на ізоморфізм.
Крок 1: Кількість вершин графа
 повинна співпадати з кількістю вершин
графа
повинна співпадати з кількістю вершин
графа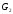 ;
;
Крок 2: Кількість ребер графа
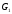 повинна співпадати з кількістю ребер
графа
повинна співпадати з кількістю ребер
графа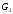 ;
;
Крок 3: Степені (півстепені) вершин графа
 повинні співпадати з степенями
(півстепенями) графа
повинні співпадати з степенями
(півстепенями) графа ,
наприклад якщо у графі є ;
,
наприклад якщо у графі є ;
Крок 4: Якщо у графі
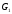 існує шлях (v1,
v2…vn)
іdeg(v1)
=k1,deg(v2)
=k2, … то і у
графі
існує шлях (v1,
v2…vn)
іdeg(v1)
=k1,deg(v2)
=k2, … то і у
графі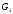 повинен існувати шлях через вершини з
степенямиk1,k2, …; Аналогічна
умова може бути сформульована і для
неорієнтованих графів.
повинен існувати шлях через вершини з
степенямиk1,k2, …; Аналогічна
умова може бути сформульована і для
неорієнтованих графів.
Крок 5: Якщо хоча б одна з цих умов не виконується, то графи не ізоморфні. Але якщо вони всі виконуються, то це не означає, що графи ізоморфні. Тоді потрібно шукати нумерацію вершин таким чином, щоби виконувалось означення 4.1. У загальному випадку таких способів є n!.Отже, кроки 1-4 допомагають швидше відповісти на запитання чи графи ізоморфні.
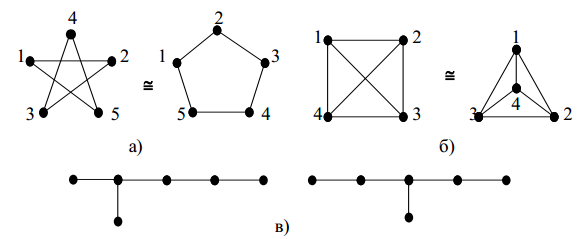
Рис. 4.2 Приклади графів
Приклад 4.2.Розглянемо рис. 4.2.
На рис. 4.2 (а,б) наведено дві пари ізоморфних графів. Графи (4.2,в) не являються ізоморфними.
Розглянемо пару графів (рис.4.2, б). Перевіримо необхідні умови ізоморфізму.
Крок 1: Кількість вершин – 6=6;
Крок 2: Кількість ребер – 5=5;
Крок 3: Сума степенів – 10=10;
Крок 4: Сума степенів сусідніх вершин співпадає, бо кожна вершина має однакову степінь.
Крок 5: Окрім цього, пронумерувавши кожну вершину графа, ми бачимо, що існує однозначне відображення кожної вершини обох графів.
Отже, графи на рис.4.2, бізоморфні.
Розглянемо пару графів (рис.4.2, в). Перевіримо необхідні умови ізоморфізму.
Крок 1: Кількість вершин – 4=4;
Крок 2: Кількість ребер – 6=6;
Крок 3: Сума степенів – 3+3+3+3=3+3+3+3; 12=12;
Крок 4-5: пронумеруємо вершини обох графів:
а) б)
Рис. 4.3 Приклад графа з пронумерованими вершинами
Як видно з рис.4.3, після нумерації вершин обох графів у графі 4.3,а є вершина 2 зі степенем deg(2)=3, сусідами якої є вершини 1, 3 та 4 зі степенями deg(1)=1, deg(3)=2, deg(4)=1 відповідно. У графі 4.3,б теж є вершина 2 зі степенем deg(2)=3, сусідами якої є вершини 1, 3 та 4 зі степенями deg(1)=2, deg(3)=2, deg(4)=1 відповідно. Отже, існує однозначної відповідності вершин, тому графи не є ізоморфними.
Для того, щоб граф
 був ізоморфним графу
був ізоморфним графу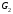 ,
необхідно і достатньо існування такої
підстановки, яка б встановлювала взаємно
однозначну відповідність між вершинами
графа, а також між їх ребрами.
,
необхідно і достатньо існування такої
підстановки, яка б встановлювала взаємно
однозначну відповідність між вершинами
графа, а також між їх ребрами.
Чи можливо встановити, чи є графи ізоморфними за їхніми матрицями інцидентності, суміжності, або списку ребер?
Для перевірки ізоморфності графів
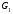 і
і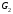 за матрицею суміжності необхідно
визначити, чи існує така перестановка
рядків і стовпців у матриці суміжності
за матрицею суміжності необхідно
визначити, чи існує така перестановка
рядків і стовпців у матриці суміжності ,
щоб у результаті вийшла матриця
,
щоб у результаті вийшла матриця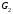 .
Із цією метою треба зробити всі можливі
перестановки рядків і стовпців (а їхня
максимальна кількість дорівнює
.
Із цією метою треба зробити всі можливі
перестановки рядків і стовпців (а їхня
максимальна кількість дорівнює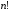 ∙
∙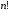 )
Якщо після однієї із цих перестановок
матриці суміжності тотожньо збігаються,
то графи ізоморфні.
)
Якщо після однієї із цих перестановок
матриці суміжності тотожньо збігаються,
то графи ізоморфні.
Для перевірки ізоморфності графів
 і
і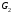 за матрицею інцидентності (і списку
ребер) необхідно визначити, чи існує
така перестановка рядків і стовпців у
матриці інцидентності
за матрицею інцидентності (і списку
ребер) необхідно визначити, чи існує
така перестановка рядків і стовпців у
матриці інцидентності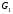 ,
щоб у результаті вийшла матриця
,
щоб у результаті вийшла матриця .
Із цією метою треба зробити всі можливі
пари перестановок рядків і стовпців (а
їхня максимальна кількість дорівнює
.
Із цією метою треба зробити всі можливі
пари перестановок рядків і стовпців (а
їхня максимальна кількість дорівнює )!
Якщо після однієї із цих перестановок
матриці інцидентності тотожно збігаються,
то графи ізоморфні.
)!
Якщо після однієї із цих перестановок
матриці інцидентності тотожно збігаються,
то графи ізоморфні.
І в першому, і в другому випадку це досить трудомісткі операції, і рішення задачі “вручну” не завжди виправдано. Найчастіше ізоморфність графів простіше встановити з їх графічних подань.
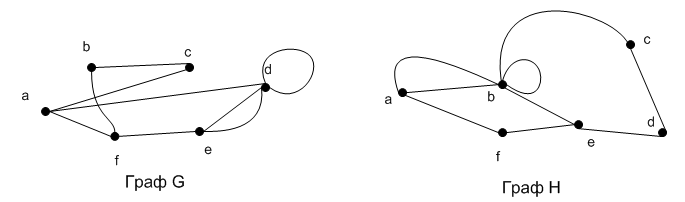
Рис.4.3 Приклади графів
Графи GіH(рис.4.3) – неорієнтовані графи з однаковою кількістю вершин і ребер. Степінь кожної вершини для цих графів опишемо в таблиці
|
Кратність у графі H |
Назва вершини |
Кратність у графі G |
|
3 |
A |
3 |
|
6 |
B |
2 |
|
2 |
C |
2 |
|
2 |
D |
5 |
|
3 |
E |
3 |
|
2 |
F |
3 |
Отже, як бачимо з таблиці степінь вершин не співпадає і графи не є ізоморфними.