Решение

Аппроксимирующую функцию

= f₁(x₁) f₂(x2)f₃(x₃)f₄(x₄)

будем искать по методу Брандона.

Нормализуем экспериментальные данные, для чего по (41) подсчитаем (или коэффициент )

и по формуле (42) найдем y_u*. Затем проведем все расчеты, необходимые для составления линейного уравнения регрессии (43), и результаты запи­шем в форме табл.15.

По формулам (8), полученным методом наименьших квадратов, опреде­ляем b₀₁ и b₁₁, то есть

f₁(x₁) = 1.0999 - 0.0077228x₁

На рис.69а изображена функция и точки y_u*, вычисленные по формуле (44), и заносим их в табл,16 вместе с данными для расчета коэффициен­тов регрессии f₂ (x₂).

Уравнение регрессии f₂ (x₂) - второй составляющей функции - име­ет вид:

f₂(x₂) = 0.8585 + 0.02123х₂.

На рисунок нанесена функция и точки y_u1=f₂(x₂). Подобную процеду­ру повторяю для нахождения функции f₃(x₃) и результаты расчетов сводят в таблицу.

Уравнение регрессии f₃(x₃) - третьей составляющей функции - имеет вид:

f₃(x₃) = 0.9791 + 0.0694x₃.

На рис.69в нанесена функция и точки y_u2=f3(x₃).

Аналогично находим f4(x4) - четвертую составляющую функции 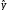, по­льзуясь табл.18, в которую для удобства занесены значения остаточной функции y_u3 и данные, необходимые для расчета f₄(x₄).

Уравнение регрессии четвертной составляющей функции имеет вид:

f₄(x₄) = 1.0466 - 0.001656x₄.

Указанная функция и точки y_u3=f₄(x₄) приведены на рис.69г.Оконча­тельно уравнение, описывающее исследуемый технологический процесс, за­писывается в виде (40):

(x₁,x₂,x₃,x₄) = 0.63 (1.0999 - 0.007228 x₁) (0.8585 + 0.02123 x₂) 3(0.9791 - 0.0694 x₃) (1.0466 - 0.001656 x₄)

После подстановки в приведенное выше уравнение экспериментальных

данных хi получим значения , которые занесены в табл.14. Сравнение экспериментальных и расчетных данные, т.е. проверку адекватности моде­ли, можно проводить способом, описанным в предыдущем примере.

Заключение

1. В рассмотренных методах форма уравнения регрессии задавалась исследователем заранее, затем определялись коэффициенты и проверялась адекватность уравнения регрессии изучаемому процессу. Дополнение урав­нения регрессии каждым новым членом требует от исследователя полного пересчета уравнения регрессии, что весьма трудоемко даже при реализации на ЭВМ.

Значительный интерес поэтому представляет задача выявления урав­нения регрессии с одновременным определением и степени полинома. Такая задача может быть решена методом последовательных приближений, когда в качестве приближения рассматривают члены полинома, а в качестве крите­рия прекращения вычислений - остаточную дисперсию каждого приближения.

Не останавливаясь подробно на методах решения указанной задачи, отметим, что значительных успехов на пути ее решения можно достигнуть, используя ортогональные полиномы Чебышева f_i (x_i), i=1,2,...,n. Тогда уравнение регрессии может быть записано в форме

= b₀f₀(x) + b₁f₁(x) + ... + b_nf_n(x) (48)

Метод построения коэффициентов регрессии с применением полиномов Чебышева дает возможность при уточнении уравнения регрессии вычислять коэффициент лишь для вновь присоединяемого члена полинома, в то время как остальные коэффициенты уравнения остаются прежними.

2. Пассивные методы сбора экспериментальных данных о работе объ­ектов химической технологии привлекают внимание многих исследователей тем, что интересующая их информация поступает в процессе нормальной эксплуатации объекта. Это преимущество значительно облегчает постанов­ку эксперимента на промышленных объектах и не усложняет взаимоотноше­ний между исследователями и технологами. В период интенсификации раз­работок математических моделей объектов химической технологии указан­ное преимущество способствовало практическому внедрению регрессионного анализа для целей изучения химико-технологических процессов на основе пассивного эксперимента. Опыт, однако, показал, что регрессионный ана­лиз, примененный при обработке данных пассивного эксперимента, не всегда приводит к эффективным результатом. И дело здесь не в самой эф­фективности классических методов регрессионного анализа, а в невыполнении исследователями его основных предпосылок.

Действительно, исследователь, приступая к изучению технологичес­кого объекта, включает в программу изучения большое число переменных факторв6 предполагая в дальнейшем отбросить некоторые из них с помощью критерия Стьюдента. При исключении незначимых факторов часть не учиты­вают, что переменные факторы коррелированы между собой (это особенно характерно для пассивного эксперимента). После пересчета уравнения регрессии оценки коэффициентов регрессии изменяются. И хотя это обсто­ятельство не оказывает существенного влияния на величину выходного па­раметра при использовании уравнения регрессии в качестве интерполяци­онного, тем не менее применить его для целей управления невозможно. Кроме того, требование регрессионного анализа, состоящее в том, что факторы хi должны измеряться с пренебрежимо малой ошибкой по сравнению с ошибкой в определении y и быть некоррелированными между собой, почти всегда нарушается при пассивном эксперименте (ошибка в их измерении часто превышает интервал изменения самих факторов).

Моделирование многомерных регрессионных задач, проведенное с по­мощью ЭВМ на искусственных примерах, продемонстрировало влияние ошибок в измерении факторов и правомерность процедуры отбрасывания факторов. В результате этого исследования показано, что ошибки при измерении факторов и их коррелированность между собой приводит к значительному ис­кажению исходного уравнения. Отсюда, конечно, не следует, что нужно полностью отказаться от пассивных методов исследования объектов хими­ческой технологии. Корреляционный и регрессионный анализы продолжают оставаться действенным средством текущего анализа производства. Но данных пассивного эксперимента, собранных при значительных ограничени­ях, высоком уровне помех и нередко низком уровне оснащенности произ­водства контролирующими приборами, явно недостаточно, чтобы построить математические модели, пригодные для управления и оптимизации техноло­гических процессов. План: