Konspekt_Lektsiy_NacherGeom_2093_DonIZhT

Рассмотрим случай, когда многогранник пересекается плоскостью общего положения. На рисунке 6.3.2 прямая трехгранная призма пересекается плоскостью, заданной двумя пересекающимися прямыми (горизонталью h и фронталью f). Поскольку ребра боковой поверхности призмы – горизонтальнопроецирующие прямые, то горизонтальные проекции точек их пересечения с плоскостью (А1, В1, С1) совпадут с одноименными проекциями самих ребер (ребра проецируются в точки, в которые также проецируются точки пересечения этих ребер с плоскостью). Нахождение фронтальных проекций точек пересечения осуществляется с помощью вспомогательных прямых 12 и 34, проведенных в плоскости f h. Т.е на π1 проводим 1121 через А1 и

3141 через В1, С1 в проекции плоскости f1 h1. Далее по линиям связи на f2 h2 находим 12, 22, 32, 42. Далее

на 1 222 по линии связи находим А2, а на 3 242 по линиям связи находим В2 и С2. В итоге АВС – контур сечения призмы плоскостью f h.

Рисунок 6.3.2

6.4 Пересечение многогранников.

Линия пересечения многогранников – замкнутая пространственная ломаная линия. Ее построение сводится к нахождению точек, в которых ребра одного многогранника пересекают грани второго и ребра второго грани первого. Т.о. многократно решается задача на пересечение прямой с плоскостью (разделы 3.7, 3.8), после чего найденные точки соединяются в линию пересечения многогранников с учетом видимости её участков относительно поверхности пересекающихся фигур.

На рис. 6.4 пересекаются прямая призма и пирамида АВСD. Боковые грани призмы – горизонтально-проецирующие плоскости, которые на π1 проецируются в прямые. Поэтому горизонтальные проекции точек пересечения ребер пирамиды с гранями призмы находятся на пересечениях их горизонтальных проекций: 11, 21, 31, 41, 51, 71. По линиям связи на фронтальных проекциях ребер пирамиды находятся

Рисунок 6.4

41

фронтальные проекции этих точек. Участки ребер пирамиды между точками их пересечения с гранями призмы (между 1 и 7, 3 и 4, 5 и 2) удаляют с чертежа, т.к в теле одного многогранника ребра другого всегда отсутствуют. Для нахождения точек пересечения (6 и 8) ребра призмы с гранями СВD и АВD пирамиды сначала определим их горизонтальные проекции: 61 и 81 совпадают с проекцией ребра призмы, т.к. оно проецируется на π1 в точку. Для нахождения вторых проекций на π1 через 61 в грани СВD (в проекции С1В1D1) проведем вспомогательную прямую DY (D1Y1), по линиям связи найдем D2Y2, на которой также по линии связи определим 62. Аналогичным образом на π1 через 81 в грани АВD (в проекции А1В1D1) проведем вспомогательную прямую DХ (D1Х1), по линиям связи найдем D2Х2, на которой также по линии связи определим 82. Участок ребра призмы между 62 и 82 удаляют с чертежа, т.к в теле одного многогранника ребра другого всегда отсутствуют. На π2 найденные точки соединяются в линии пересечения многогранников 122232 и 4252627282 с учетом видимости их участков относительно поверхности пересекающихся фигур. На π1 линии пересечения совпадают с контуром призмы. Некоторые ребра многогранников целиком или частично будут невидимы относительно поверхности фигур, что можно определить методом конкурирующих точек.

6.5 Построение разверток поверхностей многогранников.

Развертка поверхности многогранника – это плоская фигура, образованная последовательным совмещением всех его граней с одной плоскостью.

Чтобы построить развертку поверхности призмы необходимо определить н.в. (периметр) нормального сечения и н.в. ребер боковой поверхности (способ нормального сечения).

Простейший случай - развертка прямой призмы (рисунок 6.5.1 а).

Рисунок 6.5.1

Ребра основания АВС являются горизонтальными прямыми и, следовательно, на π1 они спроецированы в натуральную величину. Боковые ребра призмы занимают горизонтальнопроецирующее положение и на π2 они также спроецированы в натуральную величину. Нижнее основание АВС проецируется на π1 в н.в. и перпендикулярно боковой поверхности, т.е. может быть принято как н.в. нормального сечения. Строим (рисунок 6.5.1 б) горизонтальную прямую, на которой последовательно откладываем ребра основания (разворачиваем нормальное сечение в линию), начав и закончив с точки А0 (нижний индекс «0» будем и деле применять для разверток). Из каждой точки развернутого основания (А0, В0, С0, А0) строим

42

перпендикулярно развернутому основанию отрезки, равные высоте соответствующих ребер. Вершины соединяем ломаной линией. Для построения н.в. обоих оснований удобнее использовать метод засечек: из смежных вершин оснований радиусами, равными ребрам оснований, проводятся дуговые засечки до их пересечения…

В случае построения развертки наклонной призмы (рисунок 6.5.2 а) для получения н.в. нормального сечения проведем перпендикулярно ребрам боковой поверхности секущую плоскость Δ, которая пересечет ребра боковой поверхности в точках 1, 2, 3. Н.в. контура нормального сечения 123 найдем методом плоско-параллельного переноса, развернув фронтальную проекцию 122232 в положение параллельное оси х – 12!22!32!. При этом плоскость 123 займет положение параллельное π1, куда будет проецироваться в н.в. как 11!21!31!. При построении развертки периметр н.в. нормального сечения 11!21!31! разворачивается в горизонтальный отрезок с точками 10, 20, 30, 10 (рисунок 6.5.2 б). Перпендикулярно этому отрезку из точек 10, 20, 30, 10 вверх и вниз строят отрезки, равные соответствующим отрезкам боковых ребер призмы, отмеченным на комплексном чертеже и на развертке одинаковыми засечками.

Основания призмы параллельны π1, куда проецируется в н.в. Достроить их на развертке можно методом дуговых засечек.

Рисунок 6.5.2

Для построения развертки пирамиды необходимо иметь н.в. всех ребер (способ треугольников).

На Рисунке 6.5.3 выполнен пример построения развертки боковой поверхности пирамиды. Основание пирамиды АВС, является горизонтальной плоскостью, поэтому его проекция на π1 дана в натуральную величину. Перед построением развертки определяем н.в. всех ребер боковой поверхности методом вращения (на рисунке 6.5.3 а для примера определена только н.в. SB без указания оси вращения). Построение развертки (рисунок 6.5.3 б) начинаем с построения произвольного луча, на котором откладываем н.в. бокового ребра, например S0A0. Далее проведем из точки А0 радиусом равным н.в. АВ (измерим по А1В1) дугу до пересечения с дугой, проведенной радиусом равным н.в. SB из точки S0. На пересечении получим В0 и н.в.

43

грани АВS. Аналогично, зная н.в. всех ребер, методом дуговых засечек строим все ребра и грани, включая основание АВС. Боковая поверхность начинается и заканчивается ребромS0A0.

Рисунок 6.5.3

Вопросы для самопроверки

1.Из каких геометрических элементов складывается поверхность любого многогранника?

2.Какие основные виды многогранников вам известны?

3.Как построить неизвестную проекцию точки, лежащей на поверхности многогранника и заданной одной проекцией?

4.Какие многогранники называются правильными? Сколько граней имеет каждый из пяти видов правильных многогранников?

Задачи для самостоятельной работы

1.Построить фронтальную и горизонтальную проекции наклонной четырехгранной пирамиды с квадратным основанием 30*30 мм и высотой 55 мм. Передняя и задняя гран и призмы

горизонтально-проецирующие плоскости, параллельные	π2, левая и правая гра	ни –
фронтально-проецирующие плоскости. Наклон призмы к π1	равняется 60°.

2.Построить фронтальную и горизонтальную проекции прямой четырехгранной пирамиды с цилиндрическим отверстием. Основание пирамиды – квадрат 40*40 мм, нижнее основание

лежит в π1, две стороны которого параллельные оси проекций. Высота пирамиды 60 мм. Отверстие Ø20 мм, ось которого π2 и пересекает ось пирамиды на высоте 15 мм.

44

7. КРИВЫЕ ПОВЕРХНОСТИ

План 7.1 Основные понятия. Точки на кривых поверхностях.

7.2Пересечение поверхностей вращения плоскостью.

7.3Пересечение поверхностей вращения прямой линией.

7.1 Основные понятия. Точки на кривых поверхностях.

Кривая поверхность – это непрерывное множество последовательных положений линии, движущейся в пространстве. Линию, которая в каждом своем положении образует поверхность, называют образующей. Линию, по которой передвигается образующая (траекторию движения), называют направляющей.

Поверхности, у которых образующая – прямая линия, называют линейчатыми (прямолинейчатыми) - цилиндрические, конические, …, а у которых образующая – кривая линия, называют нелинейчатыми (криволинейчатыми) - сфера, тор, эллипсоид…

Все кривые поверхности можно также классифицировать как развертываемые, – которые можно точно развернуть в плоскость (цилиндр, конус…), и неразвертываемые - которые можно только приближенно развернуть в плоскость (сфера, тор …)

В числе кривых поверхностей – линейчатых и нелинейчатых – существуют широко распространенные в инженерной практике поверхности вращения. Поверхностью вращения

называют поверхность, полученную вращением какой-либо образующей линии вокруг неподвижной прямой оси. К ним относят цилиндр, конус, сферу, цилиндр, эллипсоид…

Для задания кривой поверхности на чертеже достаточно иметь проекции направляющей линии и указать, как строится образующая, проходящая через любую точку направляющей. Боковая поверхность прямого цилиндра (рисунок 7.1.1 а ) является горизонтальнопроецирующей и проецируется на π1 в окружность вместе со всеми точками, лежащими на ней (точки В и С). Верхнее и нижнее основания цилиндра (круги) перпендикулярны π2 и проецируются на π2 в отрезки прямых вместе со всеми точками на них лежащими (точка А).

Рисунок 7.1.1

45

Основание конуса с вершиной S (рисунок 7.1.1 б ) лежит в π1 в виде окружности, все точки которой проецируются на π2 в горизонтальный отрезок (т.В). Все образующие конической поверхности проецируются на π1 на окружность, совпадающую с проекцией основания (т. А – лежит на контурной образующей). Нахождение неизвестной проекции т. В (рисунок 7.1.1 в ) производится с помощью вспомогательной прямой (образующей 1S) или с помощью вспомогательной секущей плоскости (λ), которая пересекает конус по окружности радиуса R параллельной основанию. Проекция В1 находится по линии связи, как лежащая на 11S1 или на горизонтальной проекции контура сечения - окружности радиуса R.

Нахождение точек на поверхности сферы (центр сферы т. О) иллюстрирует рис. 7.1.2 а : по заданным проекциям 12, 22 и 31, 41 находят недостающие проекции данных точек, исходя из формы сферы. Так, заданной проекции 22, лежащей на окружности экватора поверхности сферы точки 2, соответствуют два возможных положения 21 в π1, где окружность экватора дана в н.в.

Рисунок. 7.1.2

Нахождение неизвестной проекции точки, лежащей на поверхности сферы, по одной заданной проекции осуществляется с помощью вспомогательной секущей плоскости (рисунок 7.1.2 б, в ) в следующем порядке.

1.	Через известную проекцию точки (11 на рис.		7.1.2 б и 1 2 на рис. 7.1.2 в ) задаем
	секущую плоскость η	так, чтобы её проекция (η1 на рис. 7.1.2 б и η2 на рис. 7.1.2 в)
	была параллельна оси х.
2.	Плоскость η пересечет сферу по окружности параллельной другой плоскости проекций
	(π2 на рис. 7.1.2 б	и π1 на рис. 7.1.2 в),	куда эта окружность (контур сечения)

спроецируется в н.в. вместе со всеми точками, лежащими на ней, включая точку 1. На рисунках даны только дуговые участки этой окружности радиусом Rη, измеренным на тех проекциях, где задана плоскость η по линии проекции секущей плоскости η от вертикальной оси сферы до контурной образующей.

3.Для построения неизвестной проекции точки из известной проекции проводим линию связи до пересечения с дуговым участком контура сечения.

46

7.2Пересечение поверхностей вращения плоскостью.

Взависимости от положения секущей плоскости по

отношению к цилиндрической поверхности в сечении получают (рисунок 7.2.1):

1.окружность, если секущая плоскость перпендикулярна оси цилиндра;

2.эллипс, если секущая плоскость не перпендикулярна оси цилиндра и пересекает все образующие;

3.две параллельные прямые, если секущая плоскость

параллельна оси цилиндра.

Рисунок 7.2.1

В случае, когда определены две

проекции сечения поверхности плоскостью для построения н.в. сечения используют методы преобразования комплексного чертежа. Так (рис. 7.2.2), секущая плоскость задана следом Σ2, т.е. контур сечения проецируется на π2 в отрезок 1252, а на π 1 в окружность, в которую проецируется вся цилиндрическая поверхность. Взяв произвольные точки 1-5, методом плоско-параллельного перемещения определяем н.в. сечения. Проекция сечения на π3 получена по профильным проекциям точек контура сечения, которые определены координатным способом (раздел 1.6).

Рисунок 7.2.2

В зависимости от положения секущей плоскости по отношению к конической поверхности (рисунок 7.2.3) в сечении получают:

1.окружность, если секущая плоскость перпендикулярна оси конуса;

2.эллипс, если секущая плоскость не перпендикулярна оси конуса и пересекает все образующие;

3.две пересекающиеся прямые, если секущая плоскость

проходит через две образующие и вершину конуса;

4.параболу, если секущая плоскость параллельна образующей конуса;

5.гиперболу, если секущая плоскость параллельна двум

образующим конуса и оси конической поверхности.

Рисунок 7.2.3

47

При сечении сферических и конических поверхностей проецирующей плоскостью определена только одна проекция контура сечения, которая на плоскость проекций проецируется в отрезок. Например, на рисунке 7.2.4, фронтальная проекция сечения конуса

плоскостью ∆ (заданной ∆2) проецируется в отрезок А2В2. Для нахождения горизонтальной проекции используются вспомогательные секущие плоскости (например β, с помощью которой найдены точки С и D) или вспомогательные образующие прямые (с помощью одной из которых найдены точки 1 и 2). Проекция β2 выбрана так, чтобы она делила А2В2 пополам в С2 и D2, проходя через центр и малую ось эллиптического сечения. Только после этого методом плоскопараллельного перемещения находится н.в. сечения.

Рисунок 7.2.4

Контур сечения сферических поверхностей плоскостью – всегда окружность (рисунок. 7.2.5).

В нашем случае, фронтальная проекция сечения (окружности) совпадает с секущей плоскостью Γ2, а горизонтальная проецируется в эллипс. Центр эллипса лежит на одной линии связи с серединой фронтальной проекции сечения: С2≡D2. Данный эллипс строится с помощью вспомогательных горизонтальных секущих плоскостей, каждая из которых пересекает сферу по окружности параллельной π1, и проецируется на π1 в н.в. Точки поверхности сферы, лежащие в пересечениях секущих плоскостей с Γ2, принадлежат этим окружностям. Значит горизонтальные проекции этих точек будут на пересечении контуров сечений (окружностей в н.в.) и линий связи из фронтальных проекций этих точек. Все эти точки принадлежат эллипсу. Часть эллипса выполнена пунктиром, поскольку находится в нижней, невидимой на π1 части сферы. Эта часть эллипса соответствует участку фронтальной проекции сечения от А2 до горизонтальной оси фронтальной проекции.

Рисунок. 7.2.5

48

7.3Пересечение поверхностей вращения прямой линией.

Вобщем случае построение точек пересечения прямой линии с поверхностью имеет следующий порядок построений:

1.Через прямую проводим вспомогательную секущую плоскость.

2.Строим контур сечения поверхности вспомогательной секущей плоскостью.

3.Определяем точки пересечения прямой с контуром сечения, которые и будут искомыми точками пересечения прямой с поверхностью.

Вчастном случае (рис. 7.3.1), если прямая

пересекает проецирующую поверхность, точки пересечения определяют без каких-либо построений.

Точки пересечения прямой m с горизонтальнопроецирующей боковой поверхностью цилиндра проецируются вместе с ней на π1 на окружность, где определяются их горизонтальные проекции M1 и N1 в местах пересечения окружности с m1. По линиям связи на m2 находим M2 и N2.

Рассмотрим построение точек пересечения прямой l с наклонным цилиндром, основание которого лежит в π1 (рис. 7.3.2). Проведем через l секущую плоскость параллельно оси цилиндра так, чтобы она пересекала цилиндр по прямолинейным образующим. Зададим эту плоскость двумя пересекающимися прямыми: l и KE,

Рисунок 7.3.1
проведенной		через	произвольную
точку К прямой l параллельно
образующей		цилиндра				до
пересечения		с π1 в точке Е				≡Е1.
Построим		линию	пересечения
плоскости (l		KE)	с плоскостью
основания цилиндра в π1. Для
этого через точки D≡D1 (лежит на l
в π1) и Е≡Е1		проведем в π1 прямую
DE, пересекающую				основание
цилиндра в т. 1 и 2. Из 1					1	и 21
проведем		по	поверхности
цилиндра	в	плоскости		(l	KE)
проекции	образующих			-	контур
сечения	цилиндра		плоскостью
(l KE).		Эти		проекции
образующих при пересечении с l1							Рисунок 7.3.2
дадут проекции точек пересечения l

с цилиндром: M1, N1.

49

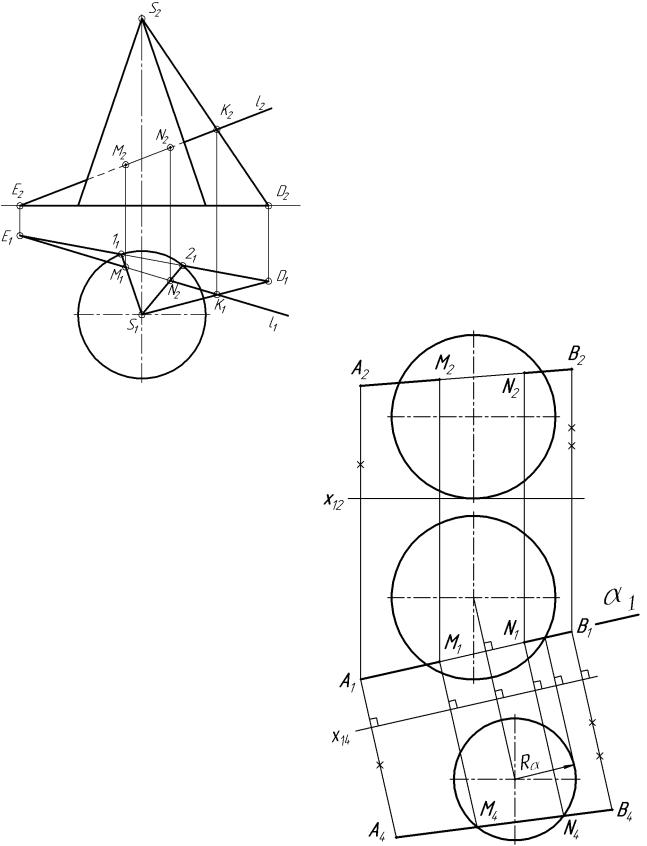
На рис. 7.3.3 выполнено построение точек пересечения прямой l общего положения с конусом, основание которого лежит в π1. Построение аналогично построению точек пересечения прямой с наклонным цилиндром. Введена вспомогательная плоскость (l KS),

проходящая через заданную прямую l и вершину конуса S. Эта плоскость пересекает π1 по прямой DE, которая пересекает основание конуса в точках 1 и 2. Проведя через 1 и 2 образующие 1S и 2S в плоскости (l KS), найдем точки пересечения 1S

и 2S с l, которые являются точками пересечения l с конусом (точки M и N).

Рисунок. 7.3.3

Определим точки пересечения прямой АВ со сферой (рис. 7.3.4). Заключим прямую АВ в горизонтальнопроецирующую плоскость α (след α1), которая пересечет сферу по окружности радиусом Rα. Введя π4 ║ α построим в π4 н.в. сечения и прямой АВ (А4В4), лежащих в α. На пересечении проекции А4В4 с окружностью сечения, получим проекции искомых точек M4 и N4. По линиям связи из

M4 и N4 (из π4 в π1) на А1В1 найдем M1 и N1. Далее на А2В2 определим M2 и N2.

Вопросы для самопроверки.

1.	Что	называется	поверхностью
	вращения?
2.	Что такое образующая?
3.	В чем различие между линейчатой и
	нелинейчатой поверхностями?
4.	Какие поверхности относится к нераз-
	вертываемым, почему?
5.	Какие кривые линии могут получатся в
	сечении прямого кругового конуса плоскостью?
6.	Каковы	общие принципы		построения	Рисунок 7.3.4
	линии	пересечения	тел	вращения с

плоскостью?

7.Как построить развертку боковой поверхности цилиндра и конуса?

8.Каков общий порядок построения точек пересечения прямой с кривой поверхностью?

50