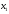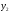3.3 Конечные разности
Пусть
функция
 задана таблицей с постоянным шагом.
Разности между значениями функции в
соседних узлах интерполяции называются
конечными разностями первого порядка:
задана таблицей с постоянным шагом.
Разности между значениями функции в
соседних узлах интерполяции называются
конечными разностями первого порядка:
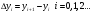
Из
конечных разностей первого порядка
образуются конечные разности второго
порядка:
 и так далее:
и так далее:
 –
конечная разность k-
того порядка (i=0,1,2...).
–
конечная разность k-
того порядка (i=0,1,2...).
Конечные
разности любого порядка могут быть
представлены через значения функции:
 ,
,

 .
.
Конечные разности принято сводить в таблицу:
Таблица 3.2
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
… |
… |
|
|
|
|
3.4 Разделенные разности
Разделенной
разностью 1-го порядка называется
отношение:
 ,
а если промежутки интерполирования
одинаковы, то
,
а если промежутки интерполирования
одинаковы, то
 .
.
Для
любого
 :
:
 ,
а если промежутки интерполирования
одинаковы, то
,
а если промежутки интерполирования
одинаковы, то

 .
.
Из
разделенных разностей первого порядка
составляют разделенные разности второго
порядка:
 .
.
Разделенной разностью второго порядка называется, для любого узла:
 .
.
Разделенной
разностью
 -го
порядка называется:
-го
порядка называется:
 ,
а для равных промежутков:
,
а для равных промежутков:
 .
.
Разделенную разность тоже принято сводить в таблицу:
Таблица 3.3
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
… |
… |
|
|
|
|
Главное свойство:
Конечные
и разделенные разности n-го
порядка от многочлена степени n
постоянны,
а
 порядка равны нулю.
порядка равны нулю.
3.5 Интерполяционный многочлен Ньютона
Пусть
для функции
 составлена таблица разделенных разностей
(3.3). Приведем без вывода формулу
интерполяционного многочлена Ньютона,
для произвольных узлов, т.е.
составлена таблица разделенных разностей
(3.3). Приведем без вывода формулу
интерполяционного многочлена Ньютона,
для произвольных узлов, т.е.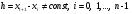 :
:
 (3.8).
(3.8).
Формула Ньютона удобна для вычисления на ЭВМ.
3.6 Интерполяционные формулы Ньютона для равных промежутков
Пусть ,
где
,
где
 .
.
Запишем интерполяционный многочлен Ньютона для неравных промежутков, заменив разделенные разности соответствующими формулами, связав их с конечными разностями.
 (3.9).
(3.9).
Обозначим
 ,
тогда
,
тогда
 получим:
получим:
 (3.10).
(3.10).
Эта формула называется первой интерполяционной формулой Ньютона для равных промежутков.
Полученное
выражение может аппроксимировать
функцию
 на
всем отрезке изменения аргумента
на
всем отрезке изменения аргумента
 .
Однако, формулу лучше использовать для
интерполирования в начале отрезка
интерполяции, то есть когда t
мало по абсолютной величине. Поэтому
первую интерполяционную формулу называют
формулой для интерполирования вперед.
.
Однако, формулу лучше использовать для
интерполирования в начале отрезка
интерполяции, то есть когда t
мало по абсолютной величине. Поэтому
первую интерполяционную формулу называют
формулой для интерполирования вперед.
Когда значение аргумента ближе к концу отрезка интерполяции, то применяют вторую интерполяционную формулу Ньютона:
 (3.11)
(3.11)
Или:
 (3.12),
здесь
(3.12),
здесь
 .
.
Вторая интерполяционная формула Ньютона называется формулой для интерполирования назад.
Заметим, что при изменении степени n у интерполяционного многочлена Ньютона, требуется только добавить или отбросить соответствующее число стандартных слагаемых. Это очень удобно на практике.
Очевидно, что при составлении интерполяционных формул Ньютона на практике можно пренебречь членами, в которых соответствующие конечные разности равны или близки к нулю. Поэтому при составлении интерполяционных многочленов вычисления обрывают на членах, содержащих такие разности, которые в пределах заданной точности можно считать постоянными.
Итак, мы получили различные записи интерполяционного многочлена. В силу единственности интерполяционного многочлена для фиксированного отрезка интерполирования изложение вопроса о погрешности метода одинаково годится как для многочлена Лагранжа, так и для многочлена Ньютона.
Остаточный член интерполяционного многочлена:
 .
.
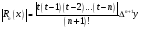 ,
,
 ,
где
,
где
 -
это максимальное значение из модулей
конечных разностей
-
это максимальное значение из модулей
конечных разностей
 -го
порядка.
-го
порядка.
Эти
формулы удобны тем, что позволяют делать
оценку ошибки метода интерполирования
без исследования
 -й
производной интерполируемой функции
-й
производной интерполируемой функции
 ,
в частности когда аналитическое выражение
ее вовсе неизвестно.
,
в частности когда аналитическое выражение
ее вовсе неизвестно.
Пример
Для функции, заданной таблично построить интерполяционные многочлены Ньютона и Лагранжа:
|
x |
-1 |
0 |
1 |
2 |
3 |
5 |
6 |
7 |
|
y |
5 |
1 |
-1 |
-1 |
1 |
5 |
19 |
29 |
Строим таблицу конечных и разделенных разностей:
|
x |
y |
|
|
|
|
|
|
-1
0
1
2
3
4
5
6
7 |
5
1
-1
-1
1
5
11
19
29 |
-4
-2
0
2
4
6
8
10 |
2
2
2
2
2
2
2 |
0
0
0
0
0
0
|
-4
-2
0
2
4
6
8
10 |
1
1
1
1
1
1
1 |
Видим, что вторые конечные (и разделенные) разности постоянны, следовательно мы будем выбирать многочлен второй степени.
Построим интерполяционный многочлен Лагранжа по формуле (3.6):
 .
.
Поскольку
шаг интерполирования постоянный, можем
использовать и формулу (3.7):
 ,
,
 ,
тогда
,
тогда
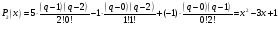
Построим
многочлен Ньютона по формуле (3.8), считая
шаг интерполяции
 ,
значения разделенных разностей возьмем
из нашей таблицы:
,
значения разделенных разностей возьмем
из нашей таблицы:
 .
.
Построим
многочлен Ньютона по формуле
интерполирования вперед (3.10):
 ,
,
 ,
,
 ,
тогда:
,
тогда: и
и
 .
.
Построим
многочлен Ньютона по формуле
интерполирования назад (3.11):
 ,
,
 ,
,
 :
:
 .
.
И,
наконец, построим многочлен Ньютона по
формуле интерполирования назад (3.11),но
 ,
,
 ,
,
 :
:
 .
.
Интерполирование
может применяться для уплотнения
заданной таблицы функции, т.е. вычисления
по исходной таблице новой таблицы с
большим числом значений аргумента на
прежнем участке его изменения. Эту
операцию называют иногда субтабулированием
функции. В
случае, когда исходная таблица является
таблицей с постоянным шагом, естественно
применять интерполяционный многочлен
Ньютона. При заданном числе узлов (т.е.
при условии, что конечные разности и
степень полинома определены вручную)
для расчетов на ЭВМ формулы Ньютона
удобно представлять по схеме Горнера.
Использование схемы Горнера позволяет
вычислять значение
 в цикле. Если же максимальный порядок
используемых конечных разностей невелик,
для вычисления значений
в цикле. Если же максимальный порядок
используемых конечных разностей невелик,
для вычисления значений
 могут использоваться формулы Ньютона
в их стандартном виде.
могут использоваться формулы Ньютона
в их стандартном виде.