1.2 Отделение корней

Первый этап численного решения уравнения состоит вотделении корней, т.е. установлении «тесных» промежутков, содержащих только один корень. Во многих случаях отделение корней можно произвести графически, например с использованием автоматизированной системы программированияMathCAD. Действительные корни уравнения (1.1) - это точки пересечения графика функциис осью абсцисс, достаточно построить графики отметить на осиотрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение (1.1) равносильным ему уравнением

(1.2).

В этом случае строятся графики функций 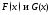, а потом на осиотмечаются отрезки, содержащие абсциссы точек пересечения этих графиков. При этом графическое отделение корней следует подкрепить вычислениями, используя следующие известные положения:

1. если непрерывная на отрезке функция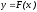принимает на его концах значения разных знаков, т.е., то уравнение имеет на этом отрезке по крайней мере один корень.

2. если функция строго монотонна, то корень на отрезке единственный.

Пример1

Для графического отделения корней уравнения можно построить график функции (см. рис. 1) и убедиться, что корень находится на отрезке. Однако для этого уравнения выгодно отдельно построить графики функцийи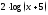(рисунок 2) и определить отрезок, содержащие абсциссу точки пересечения этих графиков. Вычислим значения функциина концах интервала:;. Первая и вторая производные на концах интервала сохраняют свои знаки:,,,, следовательно, корень на отрезкеединственный.

Рис. 1

Рис.2

1.3 Метод половинного деления

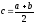Пусть уравнение (1.1.) имеет на отрезке один корень, а функцияна этом отрезке непрерывна. Суть метода состоит в построении последовательности вложенных отрезков, длина которых стремится к нулю и на концах каждого из них функцияимеет значения разных знаков. Пусть для определенности,. Разделим отрезокпополам точкой. Если, то возможно два случая: функция меняет знак на отрезкелибо на отрезке(рисунок 3). Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и, продолжая этот процесс дальше, можно дойти до сколь угодно малого отрезка, содержащего один корень уравнения. 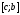На рисунке 3 видно, что корень находится на отрезке, поэтому отрезокследует отбросить, т.е. точкуперенести в точкус, - ().

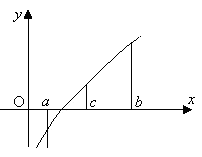
Рис. 3

На практике задают абсолютную погрешность , для определения приближенного значения корня. Если на некотором шаге деления отрезка окажется, что длина интерваластанет меньше, то любое число из этого интервала можно принять за корень уравнения. Заметим, что наn-ом шаге, длина интервала уменьшилась в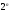раз, поэтому еще до начала решения можно определить необходимое числоnиз неравенства:.

Рис. 4

К достоинствам метода половинного деления простоту реализации метода

Недостатком данного метода является невысокая скорость сходимости.

На рисунке 4 приведена блок-схема алгоритма метода половинного деления для уравнения (1.1) на интервале .

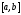4. Метод простой итерации

Заменим уравнение (1.1) равносильным ему уравнением

(1.3)

Выберем - начальное приближение к корню, подставляя его в правую часть уравнения (1.3), получим следующее приближение к корню. Теперь проделаем тоже самое с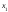, получими т.д. Вычисляя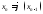, приполучим итерационную последовательностьОсновной вопрос, который необходимо выяснить: сходится ли итерационная последовательность к решению уравнения? На этот вопрос отвечает следующая теорема.

Теорема1.1. Пусть на отрезкеимеется один корень уравненияи во всех точках этого отрезка производнаяудовлетворяет неравенству. Если при этом выполняется условие, то итерационный процесс сходится, а за нулевое приближение, можно взять любое число из интервала. Это достаточные условия сходимости, т.е. существуют функции, для которых эти условия не выполняются, но, тем не менее итерационный процесс сходится.

Как следует из теоремы, при выполнении ее условий, итерационный процесс сходится при любом начальном приближении . Следовательно, полученное в итерационном процессеn-ое приближение при желании можно считать начальным. Это означает, что если в процессе вычисления приближений допускались ошибки, то они не влияют на окончательный результат. Это свойство делает метод самым надежным.

Рассмотрим геометрическое представление процесса.

При решении уравнения (1.3.) отыскивается точка пересечения кривой и прямой. Функцияможет быть какой угодно, но важно, чтобы выполнялось условие. Пусть- это корень уравнения, а- некоторое начальное приближение. На рисунке 5 изображен данный случай сходящейся последовательности.

Рис. 5

Рассмотрим другую кривую 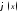, когда производная отрицательна и по модулю меньше единицы, т. е.и. Данный случай сходящейся последовательности изображен на рисунке 6.

Рис. 6

И, наконец, рассмотрим случай расходящейся последовательности, т.е. когда производная функции (рисунок 7.). В данном случае каждое последующее приближение отстоит дальше от истинного значения корня, чем предыдущее.

Рис. 7

Итак, если , то процесс сходится, если же, то итерационный процесс расходится. Отметим, что неравенства должны выполняться для всех значений, вычисляемых в ходе решения задачи.

Рассмотрим теперь вопрос об определении точности в вычисленных приближенных значений корня. Пусть - точное значение корня уравнения (1.3). Тогда для абсолютной ошибки приближения, справедливо соотношение(см. [5]). Если поставить условие, что истинное значение корня должно отличаться от приближенного на величину, т.е.,, то приближениявычисляем до тех пор, пока не будет выполнено следующее неравенство:.

Рис.8.

Для метода простой итерации на рисунке 8. приведена блок – схема алгоритма решения уравнения .

Преобразование уравнения к итерационному виду, для метода простой итерации.

Уравнение может быть приведено к видумногими способами, однако требуется сделать так, чтобы выполнялись условия:

1. функция должна быть определена и дифференцируема на,

2. для всех

3. существовало такое вещественное , чтодля всех., то полезно воспользоваться следующим приемом:

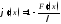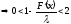Уравнение приведем к равносильному виду, где- отличный от нуля свободный параметр. В этом случае можно принять. Дифференцируя, получим. Потребуем, чтобы. Следовательно,отсюда. Если вычислить значение Мах- максимальное значение производной функциина отрезке, затем положить, а знак удолжен совпадать со знаком производной функции, то условие 3) окажется выполненным. Затем проверить условия 1-2. Таким образом, уравнениебудет приведено к итерационному виду, где.