2.4 Задание к ргр- м 2

Точка М движется в плоскости Оху (рис. 2.1, табл. 2), траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f₁ (t), у = f₂ (t), где х и у выражены в сантиметрах, t – в секундах.

Найти уравнения траектории точки; для момента времени t₁ = 1с, определить скорость и ускорение точки, а также касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории.

Зависимость х = f₂ (t) указана непосредственно на рисунках, а зависимость у = f₂ (t) дана в таблице 2 (для схем 1-3 в столбце 2, для схем 4-7 в столбце 3, для схем 8-10 в столбце 4). Номер рисунка условия в таблице М 2 – по последней.

Рисунок 2.1

Таблица 2

Номер условия	у = f2 (t)
	схема 1-3	схема 4-7	схема 8-10
1	2	3	4
0		(t – 2)^2	– 6 cos ()
1	2 – 6 cos ()
2		(4 + 2 t)^2
3		2 (t +1)^2
4
5		3 (t +1)^2 – 2
6		(t +1)^3
7
8		2 t^3
9

2.5 Пример м 2 –Кинематика точки

Даны уравнения движения точки в плоскости Оху:

(х, у – в сантиметрах, t – в секундах).

Определить уравнения траектории точки, для момента времени t₁ = 1 с. Найти скорость и ускорение точки, а также ее касательное и нормальное ускорение и радиус кривизны в соответствующей точке траектории.

Решение 1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргумент тригонометрических функций, где один аргумент вдвое больше другого, используем формулу тригонометрии.

cos 2  = 1 – 2 sin²  или (1)

из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим

следовательно

Отсюда окончательно находим следующее уравнения траектории точки (парабола, рис. 2.2).

(2)

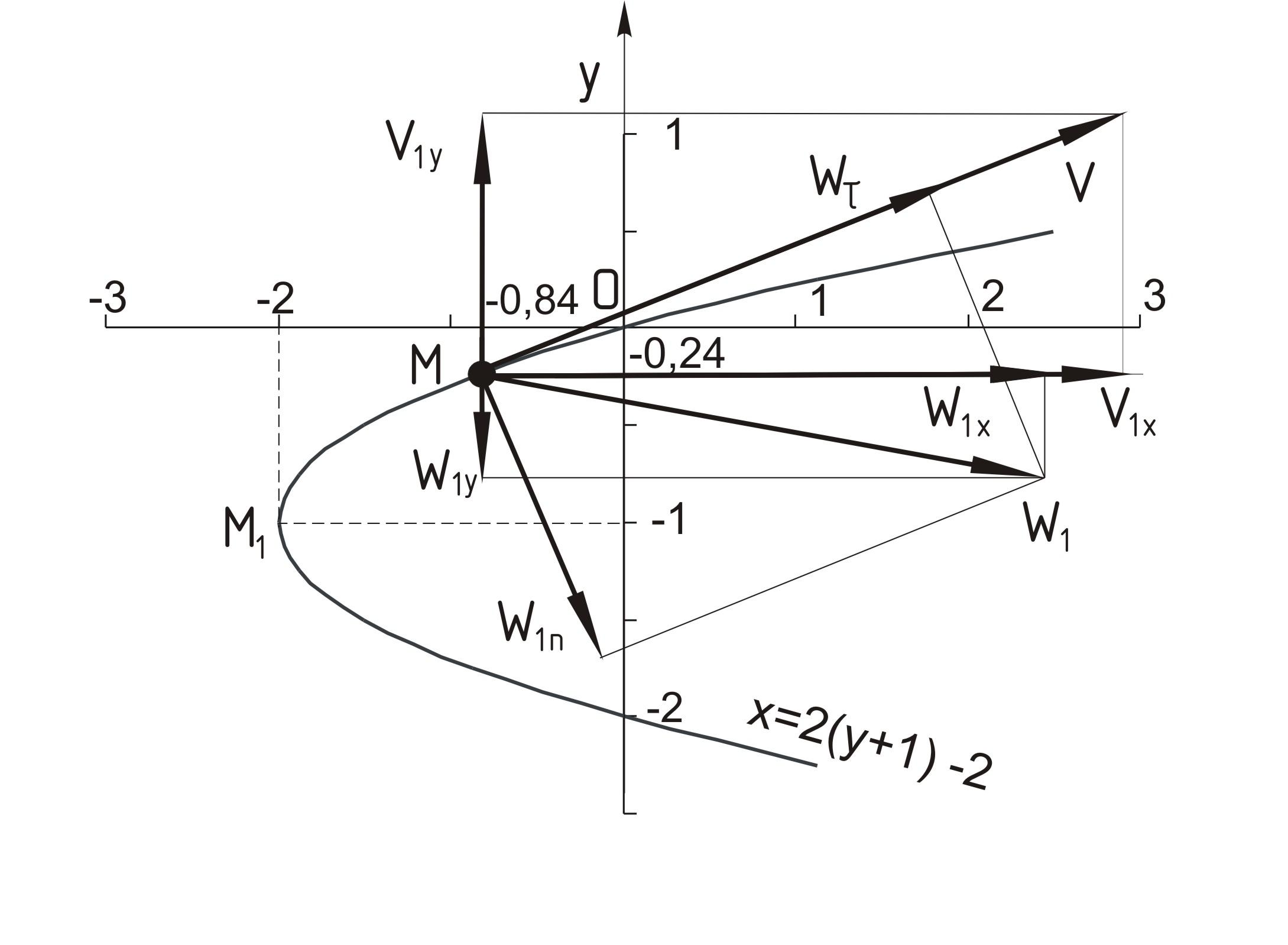
Рисунок 2.2

2. Найдем место положение точки для момента времени t = 1 с; М₁ (х₁ у₁):

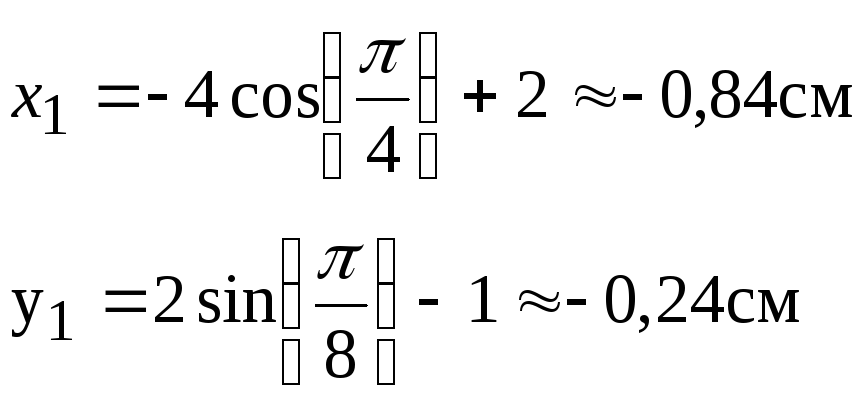
Скорость точки найдем по ее проекциям на координатные оси:

и при t = 1с.

V_1x = 2,23 см/с, V_1у = 0,72 см/с, V₁ = 2,24 см/с. (3)

3. Аналогично найдем ускорение точки:

и при t = 1с.

(4)

4. Касательное ускорение найдем, дифференцируя по времени равенство Получим:

отсюда (5)

Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив в (5) эти числа, найдем сразу, что при t = 1 с, W_1 = 1,63 см/с².

5. Нормальное ускорение точки Подставив сюда числовые значенияW₁ и W_1, получим, что при t = 1 с, W_1п = 0,66 см/с².

6. Радиус кривизны траектории Подставив сюда числовые значенияV₁ и W_1п, найдем при t = 1 с.  = 8,3 см. Полученные ответы построим схематическим на рисунке М 2. Здесь М₁ С = ₁.

3. Принцип даламбера

3.1 Принцип Даламбера для материальной точки

Принцип Даламбера устанавливает единый подход к исследованию движения любой механической системы вне зависимости от характера налагаемых на это движение условий. При этом динамическим дифференциальным уравнениям движения придается вид уравнений равновесия.

Рассмотрим несвободную материальную точку М, движущуюся по кривой АВ под действием активных сил, равнодействующая которых равна (рис. 3.1). Обозначим черезсилу реакции, с которой криваяАВ действует на точку М, значит основное уравнение динамики точки

Перенес член в правую часть равенства:

и введем в рассмотрение вектор

(3.1)

имеющий размерность силы, равный произведению массы точки на ее ускорения и направленный противоположно ускорению точки. Этот вектор называется даламберовой силой инерции, или просто силой инерции материальной точки. Тогда основное уравнение динамики примет вид

(3.2)

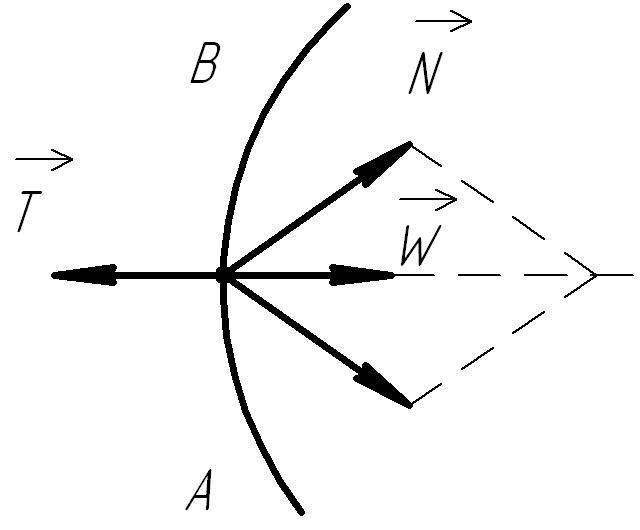
Рисунок 3.1

Силы образует сходящуюся систему сил и полученное уравнение выражает условие равновесия этой системы, что и составляет принцип Даламбера для материальной точки.

В каждый момент движения материальной точки, действующие на нее активные силы, силы реакций наложенных на точку связей и условно приложенная к точке сила инерции образуют уравновешенную систему сил.

Прикладывая силу инерции к движущейся точке, мы можем говорить лишь об условном равновесии приложенных к ней сил. Однако такая трактовка динамического уравнения движения в некоторых случаях обеспечивает наиболее простое и удобное решение задач динамики (особенно первой), и поэтому принцип Даламбера широко применяется во многих прикладных дисциплинах.