26 Условия излучения

Уравнение Гельмгольца[1]:

- имеет не единственное решение в классе (обобщённых) функций, обращающихся в нуль на бесконечности, то чтобы выделить класс единственности решения (из соображений удобства выбрать конкретное решение) в неограниченных областях, необходимо потребовать дополнительных ограничений решения на бесконечности. Этими ограничениями и явились условия излучения Зоммерфельда:

Условия излучения(1) отвечают уходящим на бесконечность волнам, а условия волнам приходящим из бесконечности. Для гармонических функций (К=0)условия излучения вытекают из единственного требования:Также можно показать, что приК0 всякое решение однородного уравнения Гельмгольца, удовлетворяющее второму из условий(1) иудовлетворяет и первому условию:

27 Зоны Френеля

Зона Френеля - это часть поверхности фронта электромагнитной волны, охватывающая вторичные источники, элементарные волны которых в точке В расходятся по фазе не более чем на 180⁰, при этом соседние зоны Френеля создают в точке В противофазные поля.

Математически размер зоны определяется выражением:

(3)Если перемещать воображаемую поверхность S вдоль линии АВ, то окружности радиуса опишут поверхности эллипсоидов вращения.

Области пространства между двумя соседними эллипсоидами вращения являются пространственными зонами Френеля (см. рисунок 3).

Несмотря на то, что площади зон Френеля

(4)

на плоскости S одинаковы, амплитуды, создаваемых ими полей в точке В убывают с ростом n, так как при этом () - уменьшается, а r'(r'') - увеличивается. Поэтому результирующее поле в точке В в основном создается волнами вторичных излучателей, расположенных в пределах первых нескольких зон Френеля.

Как показывают расчеты и эксперимент, вследствие взаимной компенсации противофазных полей соседних зон Френеля результирующее поле в точке В определяется действием лишь вторичных излучателей, расположенных в пределах 1/3 первой зоны Френеля (n = 1/3) с радиусом

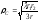. (5)

Величина имеет важное практическое значение, так как определяет размеры области существенной для распространения радиоволн.

28 Корреляционные замирания

Пространственная корреляция замираний. Если двух разнесен­ных точек приема достигают волны, распространяющиеся в достаточно разнесенных областях атмосферы, где флуктуации параметров протекают некоррелированно, то в этих двух точках приема процесс флуктуации поля протекает также некоррелированно. Статистическая связь замираний в двух пространственно-разнесенных точках описывается пространственной корреляционной функцией k(l). Поскольку статистическая связь замира­ний уменьшается по мере увеличения пространственного разноса l, то k(l) есть убывающая функция. Принято считать, что замирания статистически независимы, если k(l) убывает до значения k(l_м) = 1 / е = 0,37. Соответст­вующее значение l = l_M называетсямасштабом пространственной корреля­ции замираний. Вид функции k(l) и значение l_м зависят от механизма рас­пространения.

Частотная корреляция замираний. При одновременной передаче информации на двух частотах статистическая связь между интерференци­онными замираниями уменьшается по мере увеличения частотного разне­сения.

Это связано с тем, что пространственный набег фаз есть функция частоты поля ∆φ = 2πf∆r / c₀. Статистическая связь замираний на двух часто­тах, разнесенных на величину ∆f, описывается частотной корреляционной

функцией k(∆f). Значение ∆f = ∆f_M, при котором k(∆f) = 1 / е, называется мас­штабом частотной корреляции.

Временная корреляция замираний. Если наблюдать изменения уровней сигнала, разнесенных во времени на интервале ∆t, то по мере уве­личения ∆t обнаруживается все меньшая статистическая связь между за­мираниями, поскольку меняется мгновенная картина распределения пара­метров атмосферы. Статистическая связь замираний при временном разне­сении характеризуется временной корреляционной функцией k(∆t) зна­чением масштаба временной корреляции ∆t_М при котором k(∆t_М)  =  1 / е.