архив прош.сесий / L_3_2014_MMS_Bazova

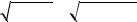
11

Середнє квадратичне відхилення дорівнює:

σ( X ) D( X ) 67, 6404 8, 224 .▲

2.3. Початкові та центральні моменти випадкової величини. Характеристики форми: ко-

ефіцієнти асиметрії та ексцесу

Узагальненням розглянутих числових характеристик випадкових величин є початкові та

центральні моменти.

Початковим моментом k-го порядку, k, випадкової величини X називають математичне сподівання величини Xk:

				ν	k	M ( X k ) (k 1, 2,3,...) .					(15)
Початковий момент 1–го порядку дає математичне сподівання ν1 M ( X ) .
Для дискретної випадкової величин X:
							n
						νk xi k pi ,
							i 1
а для неперервної:
				f (x)dx ; якщо X a;b						b
νk xk										, то νk xk f (x)dx .
										a
Центральним моментом k-того порядку, k, випадкової величини X називають матема-
тичне сподівання	k-того			степеня			відповідної			центрованої випадкової	величини,
X k ( X M (X ))k :
0
	μ	k	M ( X M ( X ))k				(k 1, 2,3,...) .				(16)
Центральний момент першого порядку дорівнює нулеві, а 2-го порядку дає дисперсію,
	μ M (X M (X )) 0; μ							2	M (X M (X ))2 D( X )
	1
Для дискретної випадкової величин X маємо:
						n
				μk (xi M ( X ))k pi ;
						i 1
а для неперервної:
										b
μk (x M ( X ))k	f (x)dx ; якщо X a;b , то μk (x M ( X ))k f (x)dx .
										a

Асиметрія та ексцес

Третій центральний момент характеризує асиметрію закону розподілу випадкової величи-

ни:

μ	M (X M (X ))3 .	(17)
3

12

Якщо випадкова величина X симетрично розподілена відносно M(X), то 3=0. Оскільки 3

має розмірність випадкової величини в кубі, то вводять безрозмірну величину – коефіцієнт аси-

метрії:

As	μ3	.	(18)
	σ3

Якщо графік щільності розподілу має правосторонню асиметрію відносно математичного очікування, то Аs>0, а коли – лівосторонню асиметрію, то Аs<0. Для нормального розподілу –

As=0 (див. наступну лекцію „Нормальний розподіл”).

Центральний момент четвертого порядку 4 використовується для визначення ексцесу, що характеризує плосковершинність або гостровершинність щільності f(x) розподілу випадкової ве-

личини. Ексцес обчислюється за формулою:

	E	μ4	3 , де	μ		M (X M (X ))4 .	(19)
		σ4			4

Для нормального закону розподілу (див. наступну лекцію) μσ44 3 Ек=0. Тому, коли

Ек>0, то графік щільності розподілу має гострішу вершину порівняно з нормальною кривою, а

якщо Ек<0 – пологішу).

Заключна частина

В лекції викладено базовий матеріал до курсу “Математичні методи в соціології ”із теорії ймовірностей: Закони розподілу суми, різниці, добутку незалежних випадкових величин. Числові характеристики випадкових величин. Показано застосування виведених формул до розв’язання прикладів.

Канд. фіз-мат. н., доцент

(О. Б. Омецінська)