
Визначення (критерій 2).
Функція
![]()
![]() називається кореляційно імунною
порядку
називається кореляційно імунною
порядку![]()
![]() ,
якщо для будь-якої сукупності
,
якщо для будь-якої сукупності
![]() номерів
номерів
![]() змінних
змінних
![]()
![]() при довільних значеннях векторів
при довільних значеннях векторів
![]()
![]() виконується співвідношення
виконується співвідношення
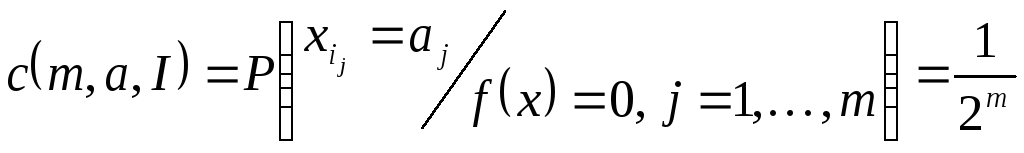 .
.
Ймовірності
![]() називаються кореляційними коефіціентами
порядка
називаються кореляційними коефіціентами
порядка
![]() функції
функції
![]() .
.
З
визначення випливає, що для аргумента
![]() ,
такого, що
,
такого, що
![]() ,
ніяка підмножина
,
ніяка підмножина
![]() з
з
![]() змінних не має особливостей, які дозволили
би обмежити варіанти їхніх значень,
виходячи з розподілу ймовірностей
змінних не має особливостей, які дозволили
би обмежити варіанти їхніх значень,
виходячи з розподілу ймовірностей
![]() .
.
Можна
довести, що функція
![]() є кореляційно імунною порядку
є кореляційно імунною порядку![]()
![]() тоді і тільки тоді, коли для її коефіціентів
Уолша-Адамара виконується умова:
тоді і тільки тоді, коли для її коефіціентів
Уолша-Адамара виконується умова:
![]()
![]()
![]() :
:
![]() .
.
Також
можна довести, що кореляційно імунна
порядку
![]() функція від
функція від
![]() змінних, є кореляційно імунною довільного
меншого порядку.
змінних, є кореляційно імунною довільного
меншого порядку.
Таким
чином, булевій функції
![]() відповідає деякий максимальний порядок
її кореляційної імунності
відповідає деякий максимальний порядок
її кореляційної імунності
![]() ,
який позначається через
,
який позначається через
![]() .
.
Раніше
ми зауважили, що функції, які досягають
максимального кореляційного імунітету
степеня
![]() ,
є афінними.
,
є афінними.
Виявляється,
якщо
![]() рівноймовірна і
рівноймовірна і
![]() ,
то функція
,
то функція
![]() афінна.
афінна.
Теорема
6.1 (Нерівність Зігенталера).
Для довільної булевої функції
![]() від
від
![]() змінних виконується нерівність
змінних виконується нерівність
![]()
![]() .
Крім того, якщо
.
Крім того, якщо
![]() - рівноймовірна і
- рівноймовірна і
![]() ,
то
,
то
![]()
![]() .
.
Для побудови булевих функцій, які задовільняють тим, чи іншим критеріям, існують відповідні методи.
Наприклад,
доведено, що якщо функції
![]() ,
,
![]() є кореляційно імунними порядку
є кореляційно імунними порядку
![]() ,
то «скомбінована» з них функція
,
то «скомбінована» з них функція
![]() від
від
![]() змінної також кореляційно імунна порядку
змінної також кореляційно імунна порядку
![]() .
.
Інший
приклад. Якщо
![]() - максимально нелінійна функція від
- максимально нелінійна функція від
![]() змінних, то функція
змінних, то функція
![]() виду
виду
![]() від
від
![]() змінних задовільняє критерій
змінних задовільняє критерій
![]() і має високу нелінійність
і має високу нелінійність
![]() ,
що задовільняє нерівність:
,
що задовільняє нерівність:
![]()
![]() .
.
Треба зауважити, що не всі кореляційно імунні функції є рівноймовірними. Таким чином, є сенс звернутися до властивостей рівноймовірних кореляційно імунних функції.
Рівноймовірні,
кореляційно імунні порядка
![]() функції називаються
функції називаються
![]() -
стабільними.
-
стабільними.
Узагальненням
![]() -
стабільних функцій є так звані стабільні
відображення.
-
стабільних функцій є так звані стабільні
відображення.
6.2 Стабільні булеві відображення
Визначення.
Відображення
![]() ,
,
![]() ,
називається
,
називається
![]() - стабільним, якщо для довільних наборів
- стабільним, якщо для довільних наборів
![]() ,
,
![]() та довільних
та довільних
![]()
![]() ,
відображення
,
відображення
![]() виду
виду
![]() є рівноймовірним.
є рівноймовірним.
У
позначенні
![]() основне навантаження несе параметр
основне навантаження несе параметр
![]() ,
оскільки він, подібно другому параметру
для критерія
,
оскільки він, подібно другому параметру
для критерія
![]() ,
задає кількість фіксованих змінних у
підфункціях координатних функцій і тим
самим визначає розмірність їхніх
аргументів:
,
задає кількість фіксованих змінних у
підфункціях координатних функцій і тим
самим визначає розмірність їхніх
аргументів:
![]() .
.
Параметри
![]() і
і
![]() показують, що
показують, що
![]() відображає
відображає
![]() -вимірні
вектори в
-вимірні
вектори в
![]() -вимірні.
Таким чином, при
-вимірні.
Таким чином, при
![]() відображення є булевою функцією.
відображення є булевою функцією.
Трійка
![]() не може бути довільною. Дійсно, згідно
із визначенням рівноймовірного булевого
відображення, образ вектор-функции
не може бути довільною. Дійсно, згідно
із визначенням рівноймовірного булевого
відображення, образ вектор-функции
![]() співпадає з
співпадає з
![]() і потужності прообразів елеменів з
і потужності прообразів елеменів з
![]() однакові. Оскільки потужність області
визначення підфункції
однакові. Оскільки потужність області
визначення підфункції
![]() дорівнює
дорівнює
![]() ,
то кожний прообраз містить
,
то кожний прообраз містить
![]() елементів, тобто, необхідно, щоб
елементів, тобто, необхідно, щоб
![]() .
.
Стабільне
відображення
![]() називається лінійним, якщо лінійні всі
його функції-компоненти.
називається лінійним, якщо лінійні всі
його функції-компоненти.
Теорема
6.2. Відображення
![]() ,
,
![]() ,
,
![]() ,
є
,
є
![]() -стабільним,
тоді і тільки тоді, коли для довільного
ненульового набора
-стабільним,
тоді і тільки тоді, коли для довільного
ненульового набора
![]()
![]() функція
функція
![]() є
є
![]() -стабільною,
тобто рівноймовірною, кореляційно
імунною порядка
-стабільною,
тобто рівноймовірною, кореляційно
імунною порядка
![]() функцією.
функцією.
Для стабільних відображень існують підходи, щодо їх побудови зі стабільних відображень меншої розмірності. Крім того практичне значення має підхід, що дозволяє будувати стабільнї відображення з лінійних стабільних відображень, виходячи з наступного твердження.
Теорема
6.3.
Нехай
![]() является
является
![]() -стабільним,
а
-стабільним,
а
![]() відображення, що здійснює перестановку
простору
відображення, що здійснює перестановку
простору
![]() .
.
Тоді
відображення
![]() також
також
![]() -стабільне
з нелінійністю
-стабільне
з нелінійністю
![]() .
.
Наведемо
приклади
![]() -стабільних
лінійних відображень.
-стабільних
лінійних відображень.
1.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
2.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Наведемо
тепер приклади обчислення кореляційних
коєфіціентів
![]() другого порядку для функції
другого порядку для функції
![]() ,
що є рівноймовірною.
,
що є рівноймовірною.
Необхідно
обчислити
 для трьох варіантів
для трьох варіантів
![]() ,
та чотирьох варіантів
,
та чотирьох варіантів
![]() .
.
Спочатку
вибираємо корені
![]() рівніння
рівніння
![]() ,
тобто аргументи у рядках, де права
частина функції дорівнює нулю.
,
тобто аргументи у рядках, де права
частина функції дорівнює нулю.
Таблиця
6.1 Корені рівняння
![]()
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
|
|
|
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
|
|
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
1 |
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
Далі
фіксуємо перший варіант для позицій
підаргумента:
![]() та підраховуемо скільки в цих позиціях
зустрічається пар
та підраховуемо скільки в цих позиціях
зустрічається пар
![]() ,
потім - скількі пар
,
потім - скількі пар
![]() ,
і так далі. Аналогічно працюємо з
позиціями підаргументу
,
і так далі. Аналогічно працюємо з
позиціями підаргументу
![]() та
та
![]() .
.
Виходячи
з того, що всього коренів
чотири, кількість всіх можливих пар
![]() дорівнює 4, обчислюємо їх ймовірності
дорівнює 4, обчислюємо їх ймовірності
![]() ,
наприклад,
,
наприклад,
![]() ,
замість
,
замість
![]() (табл 6.2). Тобто,
(табл 6.2). Тобто,
![]() не є кореляційно імунною порядка 2.
не є кореляційно імунною порядка 2.
Таблиця 6.2 Обчислення кореляційних коефіціентів
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
2 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
1 |
|
|
0 |
|
|
|
0 |
1 |
1 |
|
0 |
|
|
На завершення, слід зауважити, що стабільні функції з максимальними значеннями нелінійності, які отримуються на основі поширених методів, як правило, мають змінні, за якими вони є лінійними.
Таким чином, криптографічно стійкі булеві функції мають задовільняти відповідним критеріям на основі розумного компромісу.
