Лабораторная работа №2

Схема Бернулли.

1. Краткие теоретические сведения.

   1. Биномиальное распределение.

Пусть производится nнезависимых испытаний, в каждом из которых события А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна Р. Следовательно, вероятность непоявления события А.

q= 1 –p

Рассмотрим в качестве случайной величины Х число появлений события А в этих испытаниях. Найдем закон распределения дискретной случайной величины Х. Определим возможные значения Х и их вероятности. Очевидно, событие А в nиспытаниях может либо не появиться, либо появиться 1,2...nраз. Таким образом, возможные значения Х таковы; х₁ = 0, х₂ = 1, х₃ = 2 ... х_n+1=n.

Вероятность этих возможных значений найдем, воспользовавшись формулой Бернулли:

, (1)

где k= 0, 1, 2...n.

Формула (1) и является аналитическим выражением искомого закона распределения.

Биноминальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван биноминальным потому, что правую часть равенства (1) можно рассматривать как общий член разложения бинома Ньютона:

Таким образом, первый член разложения определяет вероятность наступления события А nраз вnнезависимых испытаниях; второй членnp^n-1qопределяет вероятность наступления событияn-1 раз; ... ; последний членqⁿопределяет вероятность того, что событие не появится ни разу.

Запишем биноминальный закон в виде таблицы:

х	0	. . .	k	. . .	n-1	n
р	q^n	. . .		. . .	n p^n-1q	p^n

2. Пуассоновское распределение.

Пусть производится nнезависимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности к появлений события в этих испытаниях используют формулу Бернулли. Если жеnвелико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р0.1).В этих случаях (nвелико, р мало) используют асимптотическую формулу Пуассона.

Найдем вероятность того, что при большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно kраз. Сделаем важное допущение: произведениеnр сохраняет постоянное значение, а именно

nр = λ.

Это означает, что среднее число появлений события А в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.

Воспользуется формулой Бернулли для вычисления вероятности появления события А к раз в nиспытаниях:

Так как nр = λ, то

Следовательно,

Принимая во внимание, что nимеет большое значение, вместоp_n(k) найдем 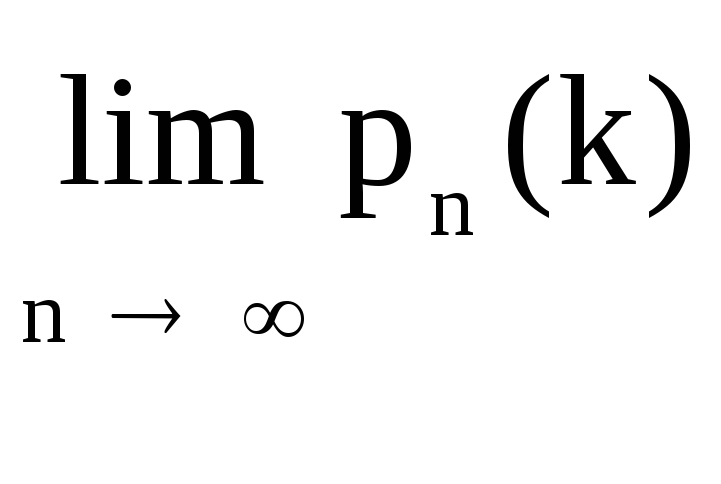. При этом будет найдено лишь приближенное значение отыскиваемой вероятности. Заметим, что поскольку произведениеnр сохраняет постоянное значение, то приn→ ∞ вероятность р→0.

Итак,

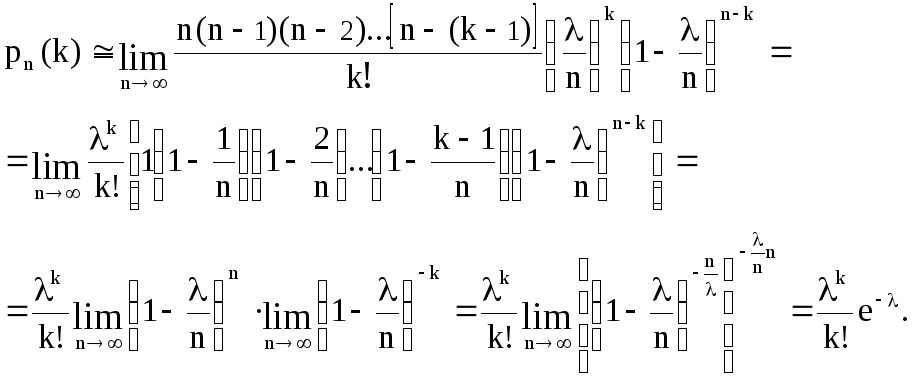
Таким образом, опуская знак приближенного равенства, получим:

Эта формула выражает закон распределения Пуассона вероятностей массовых ( nвелико ) и редких ( р мало ) событий.

3. Проверка гипотезы о распределении генеральной совокупности. Критерий согласия Пирсона.

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Иногда проводят сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. Если обследование объекта требует больших затрат, то проводить сплошное обследование не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которых производится выборка.

Объемом совокупности ( выборочной или генеральной ) называют число объектов этой совокупности.

Достаточно малую вероятность, при которой (в данной определённой задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости 0,01; 0,025; 0,05; 0,95; 0,975; 0,89.

Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.

Ограничимся описанием применения критерия χ² Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.

С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты. Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Критерий Пирсона отвечает на поставленный выше вопрос.

Пусть по выборке объема nполучено эмпирическое распределение

Варианты хi	x1	x2	. . .	xs
Эмпирические частоты ni	n1	n2	. . .	ns

Предполагая нормальное распределение генеральной совокупности, вычислим теоретические частоты n^’_і.

В качестве критерия проверки гипотезы примем случайную величину

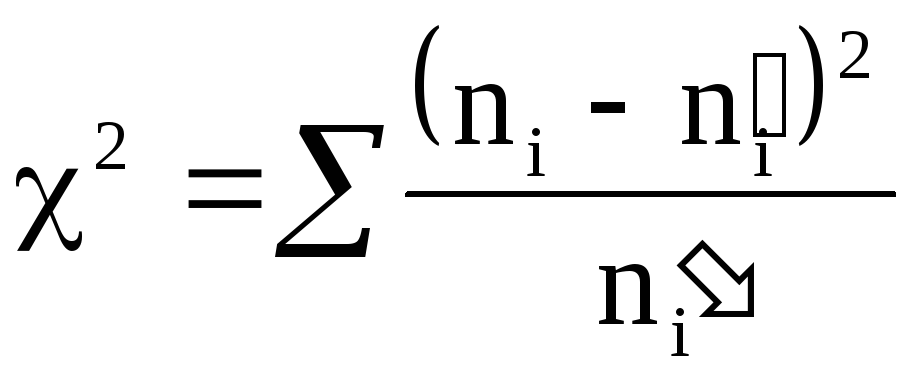
Эта величина случайная, так как в различных опытах она принимает различные, заранее не известные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия χ², и, следовательно, он в известной степени характеризует близость эмпирического и теоретического распределений.

Доказано, что при n→ ∞ закон распределения случайной величины χ² независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения χ² с r степенями свободы. Поэтому случайная величина

обозначена через χ² , а сам критерий называют критерием согласия Пирсона.

Число степеней свободы найдем так:

r = n – s - 1

Здесь n-число групп (число сравниваемых значений); s - число параметров предполагаемого распределения, которые оценены по данным выборки.

В частности, если предполагаемое распределение - нормальное, то оценивают два параметра (математическое ожидание и среднее квадратическое отклонение), поэтому s = 2 и число степеней свободы:

r = n – s - 1 = n – 2 -1 = n - 3

Если предполагают, что генеральная совокупность распределена по закону Пуассона, то оценивают один параметр λ, поэтому s = 1 и

r = n -1-1 = n - 2.

Правило: Для того, чтобы при заданном уровне значимости проверить гипотезу о распределении генеральной совокупности, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия , и по таблице критических точек распределения χ², то данному уровню значимости α и числу степеней свободы r найти критическую точку /

Если - нет оснований отвергнуть гипотезу о предполагаемом распределении случайной величины.

Если - гипотезу о предполагаемом распределении случайной величины отвергают.

Замечание 1. Объем выборки должен быть достаточно велик, не менее 50.

Каждая группа должна содержать не менее 5-8 вариант; малочисленные группы следует объединять в одну, суммируя частоты.

2. Варианты задач для заданий і и іі.

1. . Биномиальное распределение.

Задача1

Количество фамилий, начинающихся на букву К, в списках избирательных комиссий Кировоградской области в 1982 году было следующим:

Х – количество фамилий	0	1	2	3	4	5
m – количество списков	36	59	43	17	4	1

Проверить гипотезу о биномиальном распределении Х, если в каждом списке 11 фамилий.

Задача 2.

Пусть Х – количество иногородних студентов в четверке по списку. Проверить гипотезу о биномиальном распределении Х по данным в приложении 9. Списки групп объединить в одну последовательность.

Задача 3.

Пусть Х – количество студенток в четверке, идущих по списку подряд. Проверить гипотезу о биномиальном распределении Х по данным в приложении 8. Списки групп объединить в одну последовательность.

Задача 4.

Объединив списки групп Д81- 84 и Л81-82 (приложение 9 ) в одну последовательность, постройте четверки так: 1-я четверка состоит из студентов с номерами 1,2,3 и 4; 2-я соответственно 3,4,5 и 6; 3-я – 5,6,7 и 8 и так далее. Пусть Х – количество иногородних студентов в четверке по списку. Проверить согласованность Х с биномиальным законом. Чем объяснить полученные результаты.

Задача 5.

Объединив списки групп Д81- 84 и Л81-82 (приложение 8 ) в одну последовательность, постройте четверки так: 1-я четверка состоит из студентов с номерами 1,2,3 и 4; 2-я соответственно 3,4,5 и 6; 3-я – 5,6,7 и 8 и так далее. Пусть Х – количество студенток в четверке по списку. Проверить согласованность Х с биномиальным законом. Чем объяснить полученные результаты.

Задача 6.

Проверить гипотезу о биномиальном распределении количества “гербов” при бросании монеты 5раз подряд (приложение 1) по данным о бросаниях с номерами 1 – 400.

Задача 7.

Проверить гипотезу о биномиальном распределении количества “гербов” при бросании монеты 5раз подряд (приложение 1) по данным о бросаниях с номерами 201 – 600.

Задача 8.

Проверить гипотезу о биномиальном распределении количества “гербов” при бросании монеты 5раз подряд (приложение1) по данным о бросаниях с номерами 401 – 800.

Задача 9.

Проверить гипотезу о биномиальном распределении количества мальчиков в пятерке новорожденных по данным о рождениях (приложение 2) с номерами 1 – 360.

Задача 10.

Проверить гипотезу о биномиальном распределении количества мальчиков в пятерке новорожденных по данным о рождениях (приложение 2) с номерами 361 – 720.

Задача 11.

Проверить гипотезу о биномиальном распределении количества мальчиков в пятерке новорожденных по данным о рождениях (приложение 2) с номерами 721 – 1080.

Задача 12.

Пусть Х – количество снятий автобусов с рейса в АТП – 10061 в течение месяца. Проверить гипотезу о биномиальном распределении Х по данным 1 – го автоотряда:

Х	0	1	2	3	4	5
m	53	32	18	6	3	1

Задача 13.

Пусть Х – количество снятий автобусов с рейса в АТП – 10061 в течение месяца. Проверить гипотезу о биномиальном распределении Х по данным 2 – го автоотряда:

Х	0	1	2	3	4	5
m	40	28	13	4	2	1

Задача 14.

Пусть Х – количество снятий автобусов с рейса в АТП – 10061 в течение месяца. Проверить гипотезу о биномиальном распределении Х по данным 3 – го автоотряда:

Х	0	1	2	3	4	5
m	57	32	16	4	2	0

Задача 15.

Пусть Х – количество снятий автобусов с рейса в АТП – 10061 в течение месяца. Проверить гипотезу о биномиальном распределении Х по данным 4 – го автоотряда:

Х	0	1	2	3	4	5
m	50	31	19	6	3	1