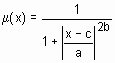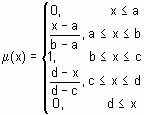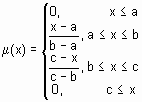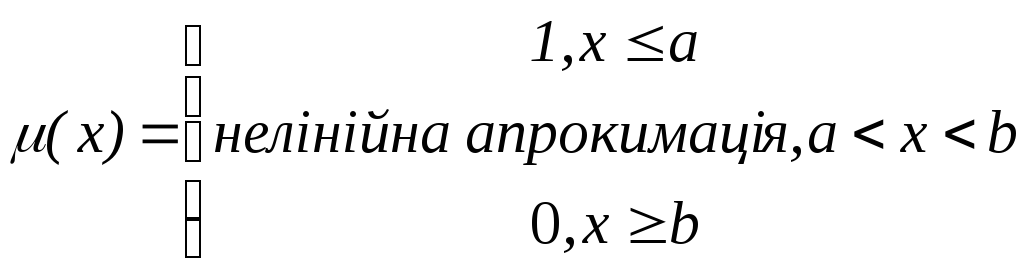Лабораторний практикум

1. Розвязок задач нечіткої математики

2. Нечіткі висновки

3. Середовище NNTOOL і його використання для розвязку прикладних задач засобами нейромереж

4. Розвязок задач апроксимації, прогнозування, класифікації та розпізнавання образів .

1. Засоби MatLab для реалізації операцій нечіткої математики

Мета роботи

1. Опанувати техніку виконання операцій нечіткої математики в середовищі Матлаб.

2. Визначити місце і роль нечіткої математики в загальному контексті штучного інтелекту та інтелектуальних систем.

Порядок виконання роботи

1. Ознайомитись з теоретичним матеріалом з відповідного розділу конспекта лек-цій та методичними вказівками до виконання лабораторної роботи.

2. Підготувати задачу відповідно до варіанта до рівня, доступного для розвязання в обраному середовищі (визначити всі потрібні функції, скласти програму).

3. Виконати тестові приклади та визначити особливості власної задачі, зокрема, вплив функції належності та методу дефадзифікації на отриманий результат.

4. Виконати складену в п.2⁰задачу, дати інтерпретацію отриманим результатам.

Склад звіту

1. Постановка задачі.

2. Програмна документація, підготовлена відповідно до вимог держстандартів України або ЄСПД.

Тестові приклади та методичні вказівки до виконання лабораторної роботи

Визначення 1. Нечітке число (НЧ) або нечітка змінна (НЗ) на дійсній прямій – це набір, що характеризується функцією належності (ФН). НЧ(НЗ) можуть бути уявленими у вигляді_А(x)/x, де знак вживається як знак об”єднання по всім x є R, _А(x) є[0,1]-ступінь належностіx є R множині .

Визначення 2. Принцип узагальнення. Хай та-НЧ на дійсній прямій R. Тоді арифметичну операцію *_f є (+, -, , /) можна представити так:

*_f =min(_А(x), _B(у))/(x*_f у)

Приклад: арифметичну операцію <приблизно 2> +_f <приблизно 6> згідно до принципа узагальнення можна уявити у такий спосіб

0/0	1/0.5	2/1	3/0.5	4/0
4/0	5/0.0.25	7/0.25	8/0.25	9/0.25		4/0.25
5/0	6/0.5	7/0.5	8/0.5	9/0		5/0.5
6/0	7/0.5	8/1	9/0.5	10/0		6/1
7/0	8/0.5	9/0.5	10/0.5	11/0		7/0.5
8/0	9/0	10/0	11/0	12/0		8/0

Результат = {6/0, 7/0.5, 8/1, 9/0.5, 10/0}. Графічне відтворення результату операції наведено нижче.

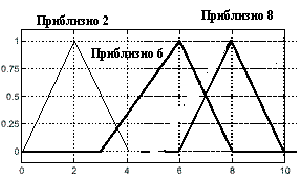
Рис. Функції належності, сформовані за допомогою

стандартних засобів MatLab – функія trimf.m

Виклик - TRIMF(X, PARAMS), PARAMS = [A B C] – триелементний вектор A <= B <= C.

Результат арифметичної операції приблизно 2 + приблизно 6, отриманий за допомогою засобів MatLab

Функція MatLab,призначена для реалізації операцій нечіткої математики, наведена нижче

function out = fuzarith(x, A, B, operator)

%FUZARITH Fuzzy arithmetics.

% C = FUZARITH(X, A, B, OPERATOR) returns a fuzzy set C as the result

% of applying OPERATOR on fuzzy sets A and B of universe X. A, B, and X

% should be vectors of the same dimension. OPERATOR should be one of the

% following strings: 'sum', 'sub', 'prod', and 'div'. The returned fuzzy

% set C is a column vector with the same length as A and B. Note that

% This function uses interval arithmetics and it assumes

% 1. A and B are convex fuzzy sets;

% 2. Membership grades of A and B outside of X are zero.

%

% Fuzzy addition could generates "divide by zero" message, but it will

% not affect the correctness of this function. (However, this may cause

% problems on machines without IEEE arithmetic, such as VAX and Cray.)

%

% For example:

x = (0:0.2:14);

A = trimf(x, [0 2 4 ]);

B = trimf(x, [4 6 8]);

C1 = fuzarith(x, A, B, 'sum');

subplot(2,2,1);

plot(x, A, x, B, x, C1);

title('fuzzy addition A+B');

grid on

C2 = fuzarith(x, B, A, 'sub');

subplot(2,2,2);

plot(x, A, x, B, x, C2);

title('fuzzy subtraction A-B');

grid on

C3 = fuzarith(x, A, B, 'prod');

subplot(2,2,3);

plot(x, A, x, B, x, C3);

title('fuzzy multiplication A*B');

grid on

C4 = fuzarith(x, B, A, 'div');

subplot(2,2,4);

plot(x, A,x, B, x, C4);

title('fuzzy division A/B');

grid on

%Roger Jang, 6-23-95

% Copyright (c) 1994-98 by The MathWorks, Inc.

% $Revision: 1.4 $

%Текст програми

x = x(:); A = A(:); B = B(:);

orig_x = x;

% augment x, A, and B for easy interpolation

A = [0; A; 0];

B = [0; B; 0];

x = [min(x)-(max(x)-min(x))/100; x; max(x)+(max(x)-min(x))/100];

tmp = find(diff(A)>0);

index1A = min(tmp):max(tmp)+1; % index for left shoulder

tmp = find(diff(A)<0);

index2A = min(tmp):max(tmp)+1; % index for right shoulder

tmp = find(diff(B)>0);

index1B = min(tmp):max(tmp)+1; % index for left shoulder

tmp = find(diff(B)<0);

index2B = min(tmp):max(tmp)+1; % index for right shoulder

height = linspace(0, 1, 101)';

index1 = find(height > max(A(index1A)));

index2 = find(height > max(A(index2A)));

index3 = find(height > max(B(index1B)));

index4 = find(height > max(B(index2B)));

height([index1; index2; index3; index4]) = [];

leftA = interp1(A(index1A), x(index1A), height, 'linear');

rightA = interp1(A(index2A), x(index2A), height, 'linear');

leftB = interp1(B(index1B), x(index1B), height, 'linear');

rightB = interp1(B(index2B), x(index2B), height, 'linear');

intervalA = [leftA rightA];

intervalB = [leftB rightB];

if strcmp(operator, 'sum'),

% interval mathematics for summation A+B

intervalC = [leftA+leftB rightA+rightB];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'sub'),

% interval mathematics for subtraction A-B

intervalC = [leftA-rightB rightA-leftB];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'prod'),

% interval mathematics for product A*B

tmp = [leftA.*leftB leftA.*rightB rightA.*leftB rightA.*rightB];

intervalC = [min(tmp')' max(tmp')'];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

elseif strcmp(operator, 'div'),

% interval mathematics for division A/B

index = (prod(intervalB')>0)'; % contains 0 or not

tmp1 = leftB.*index;

tmp = [leftA./leftB leftA./tmp1 leftA./rightB ...

rightA./leftB rightA./tmp1 rightA./rightB];

intervalC = [min(tmp')' max(tmp')'];

х1 = [intervalC(:, 1); flipud(intervalC(:, 2))];

C = [height; flipud(height)];

% get rid of inf or -inf due to division

index = find(~finite(х1));

х1(index) = [];

C(index) = [];

else

error('Unknown fuzzy arithmetic operator!');

end

% Make sure that х1 is monotonically increasing

index = find(diff(х1) == 0);

х1(index) = [];

C(index) = [];

% Take care of "out-of-bound interpolation"

index1 = find(orig_x < min(х1));

index2 = find(orig_x > max(х1));

% tmp_x is legal input for interp1

tmp_x = orig_x;

tmp_x([index1; index2]) = [];

% Do interpolation

out = interp1(х1, C, tmp_x, 'linear');

% Final output

out = [zeros(size(index1)); out; zeros(size(index2))];

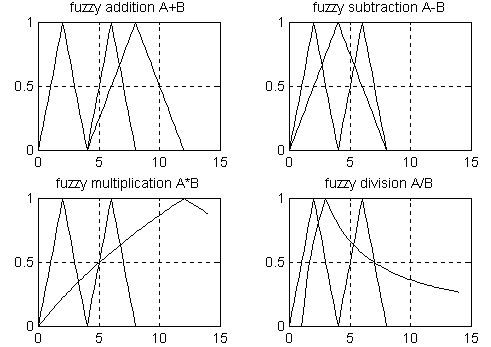
Рис. Результат роботи функції Fuzarith.m: виконання всіх

арифметичних операцій над НЧ (НЗ)

Fuzzy Logic Toolbox включає 11 убудованих функцій належностей, що використовують наступні основні функції:

• кусочно-лінійну;

• гаусовський розподіл;

• сигмоїдну криву;

• квадратичну і кубічні криві.

Для зручності імена всіх убудованих функцій належності закінчуються на mf. Вик-лик функції належності здійснюється в такий спосіб:

namemf(x, params),

де namemf – найменування функції належності; x – вектор, для координат якого необхідно розрахувати значення функції належності; params – вектор параметрів функції належності.

Найпростіші функції належності трикутна (trimf) і трапецієподібна (trapmf) форму-ється з використанням кусочно-лінійної апроксимації. Трапецієподібна функція належності є узагальнення трикутної, вона дозволяє задавати ядро нечіткої множини у вигляді інтерва-лу. У випадку трапецієподібної функції належності можлива наступна зручна інтерпрета-ція: ядро нечіткої множини – оптимістична оцінка; носій нечіткої множини – песимістична оцінка.

Дві функції належності – симетрична гаусівська (gaussmf) і двостороння гаусівська (gaussmf) формується з використанням гаусівського розподілу. Функція gaussmf дозволяє задавати асиметричні функція належності. Узагальнена дзвоноподібна функція належності (gbellmf) за своєю формою схожа на гаусівські. Ці функції належності часто використовую-ться в нечітких системах, тому що на всій області визначення вони є гладкими і приймають ненульові значення.

Функції належності sigmf, dsigmf, psigmf засновані на використанні сигмоидної кри-вої. Ці функції дозволяють формувати функції належності, значення яких починаючи з дея-кого значення аргументу і до + (-) рівні 1. Такі функції зручні для завдання лінгвістичних термов типу “високий” чи “низький”.

Поліноміальна апроксимація застосовується при формуванні функцій zmf, pimf і smf, графічні зображення яких схожі на функції sigmf, dsigmf, psigmf, відповідно.

Основна інформація про убудовані функції належності зведена в табл. 6.1. На рис. 6.1 приведені графічні зображення функцій належності, отримані за допомогою демон-страційною сценарію mfdemo. Як видно з малюнка, убудовані функції належності дозво-ляють задавати різноманітні нечіткімножини.

У Fuzzy Logic Toolbox передбачена можливість для користувача створення власної функції належності. Для цього необхідно створити m-функцію, що містить два вхідних аргументи – вектор, для координат якого необхідно розрахувати значення функції належності і вектор параметрів функції належності. Вихідним аргументом функції повинний бути вектор ступенів належності. Нижче приведена m-функція, що реалізує дзвоноподібну функцію належності :

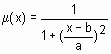function mu=bellmf(x, params) %bellmf – bell membership function; %x – input vector; %params(1) – concentration coefficient (>0); %params(2) – coordinate of maximuma. a=params(1); b=params(2); mu=1./(1+ ((x-b)/a).^2);

Рис.6.1. Убудовані функції належності

Таблиця 6.1. Функції належності

Назва функції	Опис	Аналітична формула
dsigmf	функція належностиувиглядірізниці міждвомасигмоїд-ними функціями
gauss2mf	двостороння гаусівська функція належності	якщоc1<c2, то; якщоc1>c2, то.

gaussmf	симетрична гаусівська функція належності
gbellmf	узагальненадзвоноподібнафункція принадлежности
pimf	пі-подібна функці належності	добуток smf та zmf функцій
psigmf	добуток двох сигмоїдних функцій належності
sigmf	сигмоїдна функція належносіи
smf	s-подібна функція належності
trapmf	трапецієвидна функція належності
trimf	трикутнафункцфія належності
zmf	z-подібна функція належності

Порядок параметров	№ функції належності
[a1 c1 a2 c2]	1
[c b]	2
[a b c]	3
[a b c d] [a d] – носійнечіткоїмножини; [b c] – ядро нечіткоїмножини;	4
[a1 c1 a2 c2]	5
[a c]	6
[a, b]	7
[a, b, c, d]	8
[a, b, c]	9
[a,b]	10
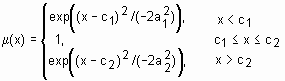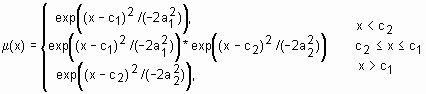