Вища геодезія для Mathcad

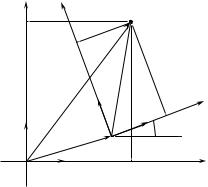
Y0	Y
y0				Q
		y
				„
				#j
				y
			„	+
			#i
	„	#„	x
		j
	#r
				#„
				i
#„				α x
j0		#„
		r
	#„			X0
	i0			x0
		Рис. 2.2

#„

#„

— базис системи XY . Нехай точка Q має координати (x0, y0) в

ри i та

j

системi X0Y0 та координати (x, y) в системi X0Y0

. Радiус-вектор

r точки Q

#„

#„

#„

#„

#„

можемо розкласти як по векторам i0, j0

, так i по векторам

i

,

j :

#„

#„

#„

#„

#„

#„

= x0

i0 +y0 j0 =

r

r +x i +y j ,

або

#„

#„

#„

#„

#„

#„

=

+

(2.1)

x0 i0

+y0

j0

x i0

y j0 +x i

+y j ,

#„

Домножимо лiву i праву частини (2.1) скалярно спочатку на

i

#„ #„

+y0

#„

#„

=

#„ #„

+

#„

#„

#„ #„

#„ #„

,

(2.2)

x0 i0· i

j0· i

x i0· i

y j0· i

+x i · i

+y j · i

а потiм на

#„

j

#„ #„

+y0

#„

#„

=

#„ #„

+

#„

#„

#„ #„

#„ #„

,

(2.3)

x0 i0· j

j0· j

x i0· j

y j0· j

+x i · j

+y j · j

та врахуємо, що

#„ #„

#„ #„

#„ #„

#„ #„

= 0

i

·

i

= j

·

j = 1,

i

j

= j

·

i

·#„

(цi спiввiдношення є наслiдком того, що

#„

#„

#„

| i | = | j

| = 1,

i

j ). Перегрупує-

мо в (2.2), (2.3) доданки i отримаємо формули, якi виражають зв’язок мiж

координатами точки Q в системах X0Y0 та XY

x = (x0 −

#„

#„

+(y0

−

#„

#„

,

(2.4)

x) i0· i

y) j0· i

y = (x0 −

#„

#„

+(y0

−

#„

#„

(2.5)

x) i0· j

y) j0· j .

(2.6)

Перепишемо їх у векторно-матричнiй формi

−

y

.

(2.7)

y =

i0· j

j0

j

!

y0

·

·

−

#„

#„

#„ #„

x0

x

i0

i

j0

i

x

#„

#„

#„

#„

21

Виразивши x0, y0 з (2.4), (2.5), отримаємо формулу для оберненого переходу

вiд x, y до x0, y0

y0

=

j0· i

j0· j

!

y

+

y .

(2.8)

#„

·

#„

#„

·

#„

x0

i0

i

i0

j

x

x

#„

#„

#„

#„

Матрицi, якi стоять в правих частинах (2.7) та (2.8), називаються матрицями повороту. Їх елементи — це косинуси кутiв мiж напрямками осей систем координат X0Y0 та XY , що випливає з властивостi скалярного добутку:

[

[

#„ #„

#„

|·|

#„

#„

#„

#„

#„

) = cos α,

i0· i

= | i0

i

| cos( i0

, i

) = cos( i0,

i

[

[

#„ #„

#„

#„

#„

#„

#„

#„

) = cos(90◦ −α) = sin α,

j0· i

= | j0

|·| i

| cos( j0

, i

) = cos( j0,

i

[

[

#„ #„

#„

#„

#„

#„

#„

#„

) = cos(α

+90◦) = − sin α,

i0· j

= | i0

|·| j

| cos( i0

, j

) = cos( i0,

j

[

[

#„ #„

#„

|·|

#„

#„

#„

#„

#„

) = cos α,

j0· j

= | j0

j

| cos( j0

, j

) = cos( j0,

j

[

#„

#„

#„

#„

i т.д.).

(тут через cos( i0

, i

) позначено косинус кута мiж векторами

i0 та

i

Таким чином, (2.7), (2.8) можемо переписати так:

y − sin α

cos α y0

−

y

x

=

cos α

sin α

x0

−

x

,

(2.9)

y0

= sin α

−cos α y +

y .

(2.10)

x0

cos

α

sin α

x

x

Матрицi повороту є ортогональними. Взагалi кажучи, матриця R називається ортогональною, якщо вона задовольняє спiввiдношенню

R−1 = RT

(2.11)

(тут R−1 означає обернену матрицю, RT — транспоновану). Серед властивостей ортогональних матриць вiдмiтимо наступнi:

1. Визначник ортогональної матрицi дорiвнює +1 або −1. Дiйсно, det(RT R) = det(R−1R) = det E = 1.

З iншого боку,

det(RT R) = det RT ·det R = (det R)2

(тут враховано, що при транспонуваннi матрицi визначник не змiнюється). Таким чином, (det R)2 = 1, тобто det R = ±1.

2.При множеннi двох векторiв на ортогональну матрицю зберiгається їх скалярний добуток. Дiйсно,

(R v1)·(R v2) = v1 R R v2		= v1	R	R v2	= v1	E v2	= v1 v2. (2.12)
#„	#„ #„T T #„	#„T	−1	#„	#„T	#„	#„ #„

3. При перетвореннi вектора шляхом його множення на ортогональну

22

матрицю зберiгається абсолютна величина вектора: h i

|R#v„|2 = (R#v„)·(R#v„) = (2.12) = #v„ #v„ = |#v„|2 |R#v„| = |#v„|. (2.13)

4.При перетвореннi двох векторiв шляхом їх множення на ортогональну матрицю зберiгається кут мiж векторами. Дiйсно,

1	2	|R v1|·|R v2|		h	i	| v1|·| v2|			1	2
#\„ #„		#„	#„			#„		#„	#\„ #„
		(R v1)	(R v2)			v1		v2
cos(R v	, R v )=	·		= (2.13), (2.12)	=		·		=cos( v	, v ).
		#„	#„			#„		#„

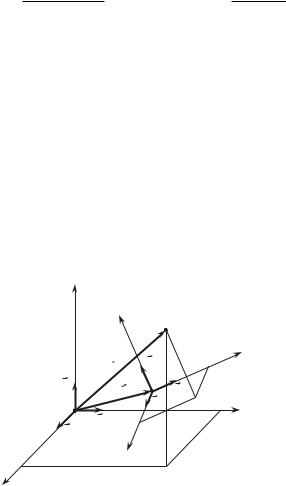
Формули (2.7) та (2.8) легко узагальнюються i на просторовий випадок, коли одна система координат змiщена та повернута вiдносно iншої

(рис. 2.3):
	x		x0	−	x
	y = R		y0	−	y .		(2.14)
	z		z0	−	z	y .	(2.15)
	y0	= RT y			+
	x0			x		x
	z0		z			z

де R — матриця вигляду	i0· j				j0· j
R =
	#„	#„			#„	#„
	i0	i			j0	i
	i0·k				j0·k
	#„	#„			#„	#„
		·#„			#„ ·#„
	#„
	Z0
			Z
						k
			r

k	r
0
	∆
	i

	j
i	0
	0
	X

#„ #„ k0· i

#„ #„ k0· j

#„ #„ k0·k

Q

j

(2.16)

Y

Y0

X0

Рис. 2.3

Нехай референцна система координат XY Z визначена в загальноземнiй

системi X0Y0Z0	положенням початку координат r = { x, y, z} та ку-
	#„

тами εx, εy, εz, на якi потрiбно послiдовно повернути систему XY Z навколо осей X,Y , Z (порядок поворотiв має значення!), щоб цi осi стали пара-

23

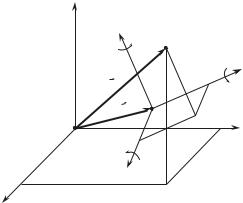
лельнi вiдповiдно осям X0,Y0, Z0 (рис. 2.4). Координати x, y, z початку референцної системи в загальноземнiй системi координат та кути εx, εy, εz

називаються елементами орiєнтування референцної системи.

В такiй постановцi координати iз однiєї системи в iншу будуть перетво-

рюватися за формулами:
X		X0 −		x
Z		Z0	−	z
µ Y	= R	Y0	−	y	,	(2.17)
X0		X			x
Y0 = µRT		Y +			y ,	(2.18)
Z0		Z			z
де µ — масштабний множник (для бiльшостi					практичних	задач можна по-

класти µ = 1), а матриця перетворення R складається з косинусiв кутiв мiж напрямками вiдповiдних осей:

		[		[		[
		cos(X0	, X)	cos(Y0	, X) cos(Z0		, X)
	cos(X0		, Z)	cos(Y0	, Z) cos(Z0		, Z)
R =		[		[		[			(2.19)
	cos(X0		,Y )	cos(Y0	,Y )	cos(Z0	,Y )
		[		[		[

Перетворення (2.18) називається перетворенням Гельмерта.

Перехiд вiд системи координат XY Z до системи X0Y0Z0 можна здiйснити трьома послiдовними поворотами системи XY Z навколо її осей X,Y , Z на

Z0
Z
εz	Q
	εy
		Y
r
r
∆
	Y0
εx
X
X0
Рис. 2.4

24

кути εx, εy, εz. Вказанi повороти описуються ортогональними матрицями

Rx =

0

cos εx

sin εx ,

Ry =

0

y

1

0

y ,

1

0

0

cos

ε

0

sin

ε

0

sin εx

−cos εx

− sin εy

0

cos εy

cos εz

sin εz

0

Rz = sin εz

−cos εz

0 ,

0

0

1

а матриця R описується серiєю поворотiв:

R=Rz ·Ry ·Rx =

=

cosεy cosεz

−cosεx sinεz +sinεx sinεy cosεz

sinεx sinεz +cosεx sinεy cosεz (2.20)

cosεy sinεz

cosεx cosεz +sinεx sinεy sinεz

−

sinεx cosεz +cosεx sinεy sinεz

−

sinεy

cosεy sinεx

cosεx cosεy

!

Формули (2.18), (2.17) є точними при довiльних величинах змiщення x, y, z та кутах повороту εx, εy, εz, але найчастiше на практицi змiщення та кути повороту осей однiєї системи координат вiдносно iншої є

що cos ε

≈

1 та sin ε

≈

ε при малих ε, i нехтую-

малими. Тому, враховуючи, 2

чи величинами порядку O(ε

), матрицю перетворення R можна наближено

замiнити матрицею

R =

εz

−1 z

εx .

e−1

1

ε

εy

−εy

εx

−1

З iншого боку, матрицю R

можна наближено замiнити матрицею

R = R =

εz

1

εx .

e

−1e

T

1

εz

−εy

e

−εy

−1−εx

1

−1

=E справджу-

Зауважимо, що для матриць R та R

властивiсть

R·R

ється

лише наближено (нехтуємо до величинами другого порядку малостi

2

e

e

e e

типу

εx, εxεy i т.п.).

ey

X0 − x

− x+X0 − zY0 + yZ0 − y z+ z y

X

1 − z

Покладаючи R ≈ R,

µ = 1, з (2.17) отримаємо

+εzX0−εxZ0 +εx

z−εz x

Y = εz

1

εx

Y0 − y = − y+Y0

Z −εy

ε

ε

ε

ε

ε

ε

εx

−1 · Z0 − z − z+Z0−εyX0 +εxY0 −εx

y+εy x

Нехтуючи величинами εx y, εy

z i т.п., якi мають другий порядок малостi,

отримаємо наближенi формули, якi зв’язують декартовi координати точок

25

в двох розглянутих системах координат:

X = − x +X0 −εzY0

Y = − y +Y0 −εxZ0Z = − z+Z0 −εyX0

+εyZ0,
+εzX0,	(2.21)
+εxY0.

	покладаючи RT			R−1, µ = 1 в (2.18) отримаємо
Аналогiчно,		X0 =		≈xe+X +εzY −εyZ,
					−
	Z0		= z+Z +εyX −εxY .							(2.22)
	Y0		=	y +Y +εxZ		εzX,
	елементи орiєнтування x,					y, z, ε	, ε	, ε		задають поло-
В (2.21), (2.22)						x	y		z

ження системи координат XY Z вiдносно системи X0Y0Z0.

Оскiльки (2.21) та (2.22) є наближеними, то пiдставивши (2.22) в (2.21) (або навпаки), ми не прийдемо до тотожностей.

2.1.1. Отримання в Mathcad виразiв для матриць повороту

Користуючись вбудованими в MATHCAD засобами символьної матема-

це показано в прикладi нижче. Спочатку оголошуються

тики, неважко отримати вирази для матрицi R та матриць R i R−1, як символьнi змiннi

e e

εx, εy, εz та задаються матрицi елементарних поворотiв Rx, Ry, Rz. Матриця R отримується шляхом множення матриць, а матрицi Rнабл та Rоб.набл, якi

вiдповiдають матрицям e i e−1, отримуються шляхом розкладання елемен-

R R

тiв матриць R та R−1 в ряд Тейлора по степенях величин εx, εy, εz. Операцiя series, яка виконує розкладання в ряд, викликається за допомогою одноiменної кнопки на панелi iнструментiв символьних перетворень. Пiсля ключового слова series через кому вказуються iмена змiнних, за якими потрiбно виконати розкладання, а число 1 — це показник найвищої степенi, до якої треба виконувати розкладання.

!"#"$%&'" ()'*"#+,- .'-,,-
εx ! 0		εx ! εx		εy ! 0	εy ! εy			εz ! 0	εz ! εz
!"#$%& '()(#("* +!),(-( ,((#.$+!"+$/ (012
#1		0	0	&	# cos εy!		0	sin εy! &	#cos εz!	"sin εz!	0 &
$		cos εx!		'	$			'	$	cos εz!	'
Rx )* $	0		"sin εx!'		Ry )* $	0	1	0 '	Rz )* $ sin εz!		0 '
$		sin εx!		'	$	"sin εy!		'	$		'
%	0		cos εx! (		%		0	cos εy!(	% 0	0	1 (

!"!#$%! &!'()*+ ,-.-(-'/
		%cos!εy" cos!εz"		cos!εz" sin!εx" sin!εy" # cos!εx" sin!εz"	sin!εx" sin!εz" $ cos!εx" cos!εz" sin!εy"(
		&		cos!εx" cos!εz" $ sin!εx" sin!εy" sin!εz"		)
R ,- Rz Ry	Rx	+ & cos!εy" sin!εz"			cos!εx" sin!εy" sin!εz" # cos!εz" sin!εx")
		&	#sin!εy"	cos!εy" sin!εx"	cos!εx" cos!εy"	)
		'				*

26

!"#$%&$' ()*+#,-(. $)!"#/.: R()*+ ()*+#,-(' 0'".1(2& $)!"#/. R , ) R'*.()*+ ()*+#,-(' 0'".1(2& $)!"#/. R 1

# 1

εz

εy

&

# 1

εz

εy &

$

'

R'*.()*+ *+ R 1

simplify

$

'

R()*+

*+ R series!"εx

!"εy

!"εz

!"1 ) $ εz

1

εx '

) $

εz

1

εx '

$

εy

εx 1

'

series!"εx!"εy!"εz!"1

$

εy

εx

1

'

%

(

%

(

!"#$!% &'$()*+ R,'"- $' R!".,'"- -)./ ,'"-)0/,! 1!(23,45 !1),)6,27 &'$()*2

(8 $!6,29$4 1! 3/-)6), :!(;1%# εx2 , εx εy 2 $.:.)

#

εy

2

2

! 1

"εx εy

"εx εz

&

$

! εz

'

$

2 ! ε

2

'

R

,'"-

R

!".,'"-

) $

"ε

x

ε

y

ε

! 1

"ε

y

ε

z

'

$

x

z

'

$

"ε

x

ε

z

"ε

y

ε

z

ε

2 ! ε

2

! 1

'

%

x

y

(

2.1.2. Числовий приклад

Отримано геодезичнi координати пункту Q в системi WGS–84:

B = 49◦ 50′ 11,4596′′,	L = 24◦ 00′ 17,1502′′,	H = 385.471 м.
Q	Q	Q

Вiдомо також параметри перетворення системи WGS–84 в деяку референцну систему:

x =	116,0 м,	εx =	0,23′′,
y =	50,5 м,	εy =	0,39′′,
z = −141,7 м,		εz = −0,47′′.

Знайти геодезичнi елiпсоїдальнi координати пункту Q в референцнiй сис-

темi.

Розв’язання

Вiд геодезичних координат переходимо до прямокутних геоцентричних

XQ = 3 765 518,398 м,

YQ = 1 676 891,973 м,

ZQ = 4 851 375,405 м.

Кути εx, εy, εz переводимо з кутових секунд в радiани, для чого просто

дiлимо кожний кут на ρ′′ =

180· 60· 60

(кiлькiсть кутових секунд в 1 рад):

π

ε

=

0,23′′

=1,115

·

10−6, ε

=

0,39′′

=1,891

·

10−6, ε

=

−0,47′′

=

−

2,279

·

10−6

,

x

y

z

ρ′′

ρ′′

ρ′′

За формулами (2.21) перейдемо вiд прямокутних координат системи WGS–84 до прямокутних координат референцної системи:

XREF = − x +XQ −εzYQ +εyZQ = 3 765 415,392 м

YREF = − y +YQ −εxZQ +εzXQ = 1 676 827,483 м

ZREF = − z+ZQ −εyXQ +εxYQ = 4 851 511,855 м

Вiд отриманих прямокутних координат (XREF,YREF, ZREF) переходимо до 27

геодезичних координат:
B	= 49◦ 50′ 17,2841′′	,	L	REF	= 24◦ 00′ 16,2991′′,	H	= 412,139 м.
REF						REF

2.2.Визначення елементiв орiєнтування референцної системи за методом найменших квадратiв

Нехай вiдомi геодезичнi координати всiх пунктiв геодезичної мережi в загальноземнiй системi i координати окремих пунктiв цiєї мережi в референцнiй системi. Треба обчислити координати решти пунктiв в референцнiй системi.

При розв’язаннi даної задачi кожен пункт Qi, (i = 1, 2, ..., n), координати якого вiдомi в двох системах координат, утворює систему рiвнянь (2.21). Шуканi параметри зв’язку двох систем координат можна обчислити, застосовуючи принцип найменших квадратiв.

Наведемо алгоритм розв’язання поставленої задачi, приймаючи, що вихiдними є геодезичнi координати B, L, H, а саме розв’язання проводиться в декартових координатах:

1.Для спiльних пунктiв виконуємо перетворення геодезичних координат B, L, H в декартовi X,Y , Z за допомогою формул (1.9).

2. Визначаємо шiсть параметрiв перетворення x, y, z та εx, εy, εz на основi формул (2.21).

3.Для пунктiв загальноземної системи координат, якi не належать до спiльних, використовуючи параметри перетворення, знаходимо координати (XREF,YREF, ZREF) в референцнiй системi.

4.Перетворюємо обчисленi в попередньому кроцi координати iз декартових (XREF,YREF, ZREF) в геодезичнi (BREF, LREF, HREF).

2.2.1.Числовий приклад

Геодезична мережа, що складається з 6 пунктiв, визначена за допомогою GPS, тобто в системi WGS–84. Для чотирьох пунктiв цiєї мережi також вiдомi координати в iншiй референцнiй системi. Знайти координати решти пунктiв в референцнiй системi.

Вихiднi данi:

28

	№	Координати в системi WGS–84
	пункту	X, м	Y , м	Z, м
	1	3 891 691,256	1 664 649,670	4 756 306,789
	2	3 889 361,816	1 652 561,209	4 762 349,442
	3	3 895 858,994	1 650 121,207	4 757 276,785
	4	3 899 316,609	1 666 588,016	4 749 812,656
	5	3 893 263,494	1 651 584,261	4 759 060,129
	6	3 893 410,399	1 648 738,258	4 759 792,799
	№	Координати в референцнiй системi
	пункту	XREF, м	YREF, м	ZREF, м
	1	3 891 663,852	1 664 770,797	4 756 382,194
	2	3 889 334,581	1 652 682,848	4 762 425,230
	3	3 895 831,667	1 650 242,782	4 757 352,453
	4	3 899 289,330	1 666 708,959	4 749 888,199
	5	?	?	?
	6	?	?	?

Нижче наведенi тi ж самi данi в бiльш зручному для копiювання форматi:

3891691.256 1664649.670 4756306.789

3889361.816 1652561.209 4762349.442

3895858.994 1650121.207 4757276.785

3899316.609 1666588.016 4749812.656

3893263.494 1651584.261 4759060.129

3893410.399 1648738.258 4759792.799

3891663.852 1664770.797 4756382.194

3889334.581 1652682.848 4762425.230

3895831.667 1650242.782 4757352.453

3899289.330 1666708.959 4749888.199

Розв’язання

Кожен пункт Qi (i = 1, ..., 6), координати якого вiдомi в двох системах, утворює систему з трьох рiвнянь вигляду (2.21) з шiстьма невiдомими — x, y, z, εx, εy, εz — параметрами зв’язку двох систем координат. Отже, для знаходження невiдомих достатньо мати лише два пункти. При бiльшiй кiлькостi пунктiв з вiдомими координатами в обох системах (в нашому випадку таких пунктiв чотири) вказанi невiдомi можна знайти, застосовуючи

принцип найменших квадратiв.

Запишемо систему рiвнянь (2.21) для пунктiв 1, 2, 3, 4

29

y

+Z1εx

−Z1εy

−X1

εz

=

Y1

−Y1REF

,

x

+Y1

εz

=

X1

−X1REF

,

−

−

x

Z2εy

+Y2εz

=

X2

X2REF,

z

Y1εx +X1εy

=

Z1

Z1REF,

−

−

y

+Z2εx

X2εz

=

Y2

Y2REF,

−

−

z

Y2εx

+X2εy

=

Z2

Z2REF,

−

−

x

Z ε

+Y ε = X X ,

−

−

(2.23)

z

Y3εx

+X3εy

−

=

Z3

−Z3REF

,

3

y

3

z

3

3REF

−

−

y

+Z3εx

X3εz

=

Y3

Y3REF,

x

Z4εy

+Y4εz = X4

X ,

−

−

y

+Z εx

X εz = Y Y ,

z

Y ε

+X ε

−

−

= Z Z .

4REF

−

−

4

4

4

4REF

4

x

4

y

4

4REF

Перепишемо (2.23) в матричнiй формi:

#„

#„

(2.24)

де введено позначення:

M· v = b,

−

0

X1

Y1

−Y1REF

0

1

0

Z1

1

0

0

0

Z1

Y1

X1

X1REF

0

0

1

−Y1

X1

−

0

Z1

−Z1REF

1

0

0

0

Z2

Y2

x

X2

X2REF

−

y

−

0

1

0

Z2

0

−X2

Y2

−Y2REF

0

1

Y2

X2

0

#„

z

#„

Z2REF

0

,

Z2

M = 1 0 0

− 0

Z

Y

,

v

=

ε

b =

X

−X

0 1 0

Z

−

0

−

X

ε

Y

−Y

0

1

Y3

X3

0

εz

−

Z3REF

0

Z3

−

3

3

x

3

−

3REF

0

0

Z4

Y4

X4REF

1

0

y

X4

3

3

3

3REF

1

0

Z4

−

0

X4

−

Y4REF

0

−

Y4

−

0

1

Y4

X4

0

Z4REF

0

Z4

−

−

В загальному

випадку задовольнити

шiстьма невiдомими дванадцяти

рiв-

нянням (2.23) неможливо. Пiдставивши в (2.24) будь-який вектор v , отри-
					#„
маємо ненульовий вектор нев’язок s =	#„ ·		−	#„
		#„			. Але можна знайти такi
#„				b
	M v

значення невiдомих компонент вектора v , якi б мiнiмiзували суму квадра-

тiв елементiв вектора нев’язок s . Згiдно з методом найменших квадратiв,
#„
такий розв’язок дається формулою
#„	T	·M)	−1		T	#„	(2.25)
v = (M				·M		· b
Пiдставимо в (2.25) числовi	значення				з	таблиць,	наведених в умовi

30