Вища геодезія для Mathcad

Обчислюємо довжину дуги за формулою (4.16):			= 444 157,729 м
Sм = Mm(B2 −B1)	1 + 8 (B2 −B1)2 cos 2Bm
		e2

Обчислюємо довжину дуги за формулою (4.18):

Sм = 16 (B2 −B1)(M1 + 4Mm + M2) = 444 157,744 м

Нарештi, скористаємось MATHCAD для чисельного обрахунку значення iнтегралу (4.14). В наведеному нижче прикладi виконується глобальне присвоєння змiннiй TOL, яка задає точнiсть обчислень. Значення цiєї змiнної можна задавати або безпосереднiм присвоєнням в MATHCAD -документi, або на вкладцi Встроенные переменные дiалогового вiкна Параметры документа (воно викликається через пункт меню Инструменты Параметры документа). Однак в даному прикладi присвоєння змiннiй TOL носить скорiше iлюстративний характер, оскiльки пiдiнтегральний вираз досить “зручний” для чисельного iнтегрування (не має особливих точок на промiжку iнтегрування).

ǹ ȣȓȒȈ:D:\GEODETICLIB.XMCDZ(R)

ǹ ȣȓȒȈ:D:\WGS84_DATA.XMCDZ

ɉɟɪɟɜɨɞɢɦɨ ɲɢɪɨɬɢ ɡ ɝɪɚɞɭɫɧɨʀ ɦɿɪɢ ɜ ɪɚɞɿɚɧɧɭ

B1		dms2rad(45 30 17.221)		0.794208299421444
B2		dms2rad(49 29 58.938)		0.8639328310159
Ɂɚɞɚɽɦɨ ɬɨɱɧɿɫɬɶ ɨɛɱɢɫɥɟɧɧɹ
TOL { 0.0001
Ɉɛɱɢɫɥɸɽɦɨ ɞɨɜɠɢɧɭ ɞɭɝɢ ɹɤ ɿɧɬɟɝɪɚɥ
s		a 1 e2 µ´B2	1				dB 444157.7437442423
ɦ		µ			3
		µ	1 e2 sin(B)2		2
		µ
		¶B1

4.3.2. Приклад обчислення довжини дуги паралелi

Для′

елiпсоїда WGS–84 обчислити довжину дуги паралелi L

2 −

L =

0

◦

′′

на широтi B = 54

◦

32

′

19,354

′′

.

1

45 46,882

Розв’язання

Переводимо рiзницю довгот та широту з градусної мiри в радiанну:

L2 −L1 = 0,0133172597,

B = 0,9518800496

61

Обчислюємо довжину дуги за формулою (4.13):

a cos B	= 49 387,569 м.
sп = (L2 −L1) p1 −e2 sin2 B

4.4. Площа сфероїдичної трапецiї

Сфероїдична трапецiя являє собою дiлянку поверхнi земного елiпсоїда, обмежену меридiанами та паралелями. На рис. 4.5 сторонами нескiнченно малої трапецiї ABCD є елементи дуг меридiанiв та паралелей:

AD = BC = MdB, AB = CD = N cos BdL;

тодi площа буде

a2(1 −e2) cos B

dP = MN cos B dB dL = (1 −e2 sin2 B)2 dB dL

Площа скiнченої трапецiї, обмеженої широтами B1 i B2 та довготами L1 i L2 виражається подвiйним iнтегралом

L2 B2
P = a2(1 −e2) Z	Z			cos B				dB dL		(4.21)
		(1	−	e2 sin2 B)2
L1	B1
звiдки, iнтегруючи по L, попередньо знайдемо
			B2
P = a2(1 −e2)(L2 −L1) Z						cos B			dB.
				(1	−	e2 sin2		B)2
		B1

Iнтеграл в правiй частинi цiєї рiвностi може бути виражений в елементарних функцiях. Користуючись пiдстановкою e sin B = sin t (звiдки

B

A

C

D

Рис. 4.5. Сфероїдична трапецiя

62

e cos B dB = cos t dt), знаходимо

Z

cos3 t

= 2e cos2 t + ln 1 cos t

.

Z

(1 −e2 sin2 B)2 dB = e

cos B

1

dt

1

sin t

+ sin t

Повертаючись до змiнної B, остаточно отримаємо

e sin B

B1

(4.22)

P = 2 a2

(1 −e2)(L2 −L1)

1

e2 sin2

B

+ 2e ln 1

1

sin B

1

1 + e sin B

B2

|

B2

−

−

2

|B1

Запис

...

означає, що

вираз потрiбно спочатку обчислити при B = B ,

потiм при B = B1, а отриманi значення вiдняти.

Для отримання наближеної формули розкладемо пiдiнтегральний вираз

в (4.21) в ряд за степенями e i виконаємо почленне iнтегрування:

2

2

(sin B

sin B ) +

2

2

(sin

3

sin

3

B )+

P

a

e

L

L

e

B

=

(1 −

)(

2 −

1) h

3

2 −

1

3

4

2

−

1

+

e4(sin5 B2 −sin5 B1) +

e6(sin7 B2 −sin7 B1) + . . .

5

7

Знайдемо площу всiєї поверхнi елiпсоїда. Для цього в

(4.21) слiд поi-

класти L2 − L1 = 2π,

B1 = 0,

B2 =

π

та

отриманий

результат подвоїти. В

2

результатi отримаємо:

−

h

3

5

7

i

2

− 2e

1 + e

P = πa2

e

1

ln

1 −e

+ 1 = 4πa2(1

e2) 1 +

2

e2 +

3

e4

+

4

e6 + . . . .

(4.23)

4.5. Геодезична лiнiя на поверхнi елiпсоїда

Запишемо систему диференцiальних рiвнянь, якi описують геодезичну лiнiю на поверхнi елiпсоїда. Для цього потрiбно в (3.34) з врахуванням (4.4) пiдставити

u → B, v → L,

θ → A,

#„

#„

#„

#„

| ru

| → | r B| = M, | rv| → | r L| = N cos B.

Отримаємо:

ds

=

M

,

dB

cos A

=

,

sin A

dL

= tg B sin A,

(4.24)

dA

ds

N cos B

ds

N

де A — геодезичний

(кут мiж геодезичною лiнiєю та дотичною,

азимут

проведеною до меридiану в пiвнiчному напрямку).

Роздiлимо перше рiвняння системи (4.24) на третє:

dB

=

N cos A

=

1 −e2 sin2 B

cos A

,

(4.25)

dA

(1 −e2) tg B

M tg B sin A

· sin A

63

а пiсля роздiлення змiнних матимемо:

(1 −e2) tg B

dB =

cos A

dA.

(4.26)

sin A

1 −e2 sin2 B

Проiнтегруємо лiву та праву частини (4.26)

(1 −e2) tg B

dB =

cos A

dA

i отримаємо

Z 1 −e2 sin2 B

Z

sin A

= ln(sin A) +C ,

ln

p

1 −e2 sin2 B

(4.27)

де C

cos B

C

iншу сталу C за правилом

— стала iнтегрування. Ввiвши замiсть

C = ln

a

, перетворимо (4.27)

C

p

ln

1 −e2 sin2 B

= ln(sin A) + ln

a

= ln

a sin A

cos B

C

C

1 −e2 sin2 B

= a sin A

a cos B sin A = C

p cos B

C

1

−

e2 sin2

B

i отримаємо формулу Клеро

p

N cos B sin A= const,

(4.28)

яка показує, що добуток радiуса паралелi Rп = N cos B на синус азимута в будь-якiй точцi геодезичної лiнiї є величиною сталою.

Формула Клеро дозволяє якiсно прослiдкувати хiд геодезичної лiнiї на елiпсоїдi при будь-якiй її протяжностi. Нехай геодезична лiнiя починається вiд деякої точки з широтою B > 0 i азимутом 0◦ < A < 90◦. Переходячи до точки з бiльшою широтою, тобто з меншим радiусом паралелi, приходимо до висновку, що для сталостi добутку (4.28) необхiдно, щоб збiльшилось значення sin A, а отже, i значення A. В деякiй точцi з широтою +B0 значення sin A досягне свого максимуму, тобто 1, а азимут буде дорiвнювати 90◦, тобто геодезична лiнiя буде дотикатися деякої паралелi (рис. 4.6). Пiсля цього вздовж геодезичної азимут почне збiльшуватись, починаючи з 90◦, а sin A — зменшуватись. Таке збiльшення азимуту буде продовжуватись до екватора, де радiус паралелi досягне найбiльшої величини, sin A

— найменшої величини, а азимут A — найбiльшої. Нижче екватора поведiнка геодезичної лiнiї буде дзеркальним вiдображенням її поведiнки в пiвнiчнiй половинi елiпсоїда. Прослiдковуючи шлях геодезичної, приходимо до висновку, що геодезична лiнiя буде описувати на елiпсоїдi нескiнчену кiлькiсть обертiв, послiдовно дотикаючись двох паралелей з широтами +B0

та −B0.

Неважко бачити, що меридiан є частковим випадком геодезичної лiнiї.

64

B0

–B0

Рис. 4.6. Шлях геодезичної лiнiї на поверхнi елiпсоїда

Дiйсно, пiдставляючи A(s) = 0 в (4.24), отримаємо:

	dB	=	1	,		dL		= 0,	dA		= 0,
	ds		M			ds			ds
звiдки маємо розв’язок
s = Z B M dB,					L = L0 = const,						A= 0.

B0

Випишемо формули для кривизни та кручення геодезичної лiнiї:

k =		cos2 A			+	sin2 A	,
κ =	N		M			N
			− M	sin Acos A.
	1		1

(4.29)

(4.30)

65

5. Розв’язання геодезичних задач на сферi

5.1. Постановка задач

Розв’язання геодезичних задач на поверхнi сфери або елiпсоїда полягає у визначеннi геодезичних координат деякої точки по заданим координатам iнших точок та по вимiряним чи заданим кутовим та лiнiйним величинам.

Оскiльки сфера є частковим випадком елiпсоїда, тому сформулюємо геодезичнi задачi саме для елiпсоїда; для сфери їх постановка iдентична.

Нехай мiж двома точками Q1 i Q2 (рис. 5.1) на поверхнi елiпсоїда проведено геодезичну лiнiю. Домовимося точку Q1 розглядати як початкову точку геодезичної лiнiї, а Q2 — як кiнцеву. Геодезична лiнiя вiд точки Q1 до точки Q2 має прямий напрямок, а вiд Q2 до Q1 — обернений. В будь-якiй точцi геодезичної лiнiї її азимут називається прямим, якщо вiн показує прямий напрямок геодезичної, i оберненим, якщо вiн вказує обернений напрямок цiєї лiнiї. Таким чином, прямий та обернений азимути в однiй i тiй самiй точцi вiдрiзняють один вiд одного на 180◦. Прямий азимут в точцi Q1 називається початковим азимутом геодезичної лiнiї.

Пряма геодезична задача. Дано геодезичнi координати B1, L1 точки Q1, розташованої на поверхнi елiпсоїда, а також довжина геодезичної лiнiї s та її початковий азимут A1. Потрiбно знайти координати B2 i L2 та обернений азимут A2 в точцi Q2.

Обернена геодезична задача. Дано геодезичнi координати B1, L1 та B2, L2 двох точок Q1 та Q2. Потрiбно знайти найкоротшу вiдстань s (довжину геодезичної лiнiї) мiж заданими точками, а також прямий A1 та обернений

A2 азимути цiєї лiнiї в точках Q1 i Q2.
Кутова засiчка. Дано геодезичнi координати		двох точок Q1 та Q2
P		P
l
			Q3
Q2			s23
	A2		s13
A1 s			A23
			A13
Q1		Q1	Q2
			s12

Рис. 5.1

Рис. 5.2

66

(рис. 5.2), а також напрямки з цих точок на третю точку Q3 (азимути A13, A23). Лiнiями, для яких заданi напрямки, можуть бути геодезичнi лiнiї, нормальнi перерiзи та iн. Необхiдно знайти геодезичнi координати точки Q3.

Лiнiйна засiчка. Дано геодезичнi координати двох точок Q1 та Q2 (рис. 5.2), а також довжини геодезичних лiнiй s13, s23, що з’єднують точки Q1, Q2 з точкою Q3. Необхiдно знайти геодезичнi координати точки Q3.

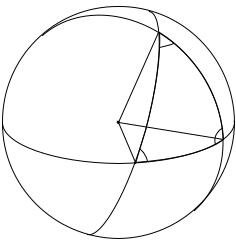
5.2. Сферичний трикутник

Якщо перетнути сферу площиною, яка проходить через її центр, то в перетинi отримаємо велике коло, радiус якого дорiвнює радiусу сфери. Очевидно, через двi точки на поверхнi сфери можна провести тiльки одне велике коло, якщо, звичайно, цi точки не лежать на протилежних кiнцях дiаметру. Три точки A, B, C на поверхнi сфери можна з’єднати дугами великих кiл i тим самим отримати сферичний трикутник (рис. 5.3). Довжини сторiн сферичного трикутника позначимо через a, b, c, а протилежнi ним кути, пiд якими перетинаються дуги, що утворюють сторони трикутника,

— через α, β, γ. Надалi будемо розглядати сферичнi трикутники, у яких кути α, β, γ меншi вiд π; такi трикутники називаються трикутниками

Ейлера.

A

D

		b
	c
O
	E	C
B		a

Рис. 5.3. Сферичний трикутник

Кожному сферичному трикутнику вiдповiдає тригранний кут з вершиною O в центрi сфери та ребрами OA, OB, OC. Довжини сторiн сферичного трикутника пропорцiйнi вiдповiдним плоским кутам вказаного тригранника (цi кути називають центральними). Так, наприклад, якщо BOC = ϕ, при-

67

чому кут ϕ виражений в радiанах, то сторону a можна знайти як a = Rϕ,

де R — радiус сфери. Таким чином, вiдношення Ra , Rb , Rc вiдповiдно дорiвнюють центральним кутам BOC, AOC, AOB, вираженим в радiаннiй мiрi.

Укажемо основнi властивостi сферичних трикутникiв:

1.Сума двох сторiн бiльша вiд третьої сторони, рiзниця двох сторiн менша вiд третьої сторони:

a+ b > c, |a−b| < c.

2.Сума двох кутiв менша, нiж третiй кут, збiльшений на π:

α+ β < γ + π.

3.Сума кутiв лежить в межах вiд π та 3π, а сума сторiн лежить мiж 0 та 2πR:

π < α+ β + γ < 3π, 0 < a+ b + c < 2πR.

4.Величина ε, на яку сума кутiв перевищує π, називається сферичним надлишком або ексцесом:

ε = α+ β + γ −π.

Площа сферичного трикутника виражається через його ексцес:

S= εR2.

5.3.Розв’язання сферичних трикутникiв

Для розв’язання сферичного трикутника iснують рiзнi формули сферичної тригонометрiї; серед них виберемо наступнi:

Теорема синусiв

sin	a			sin	b			sin	c
	R		=		R		=		R		.
sin α				sin β
								sin γ

Теорема косинусiв сторiн

cos Rc = cos Ra cos Rb + sin Ra sin Rb cos γ, cos Ra = cos Rb cos Rc + sin Rb sin Rc cos α,

cos Rb = cos Rc cos Ra + sin Rc sin Ra cos β.

Теорема косинусiв кутiв

cos α = sin γ sin β cos Ra −cos γ cos β,

(5.1)

(5.2)

(5.3)

(5.4)

(5.5)

cos β = sin α sin γ cos	b	−cos α cos γ,	(5.6)
	R
cos γ = sin β sin α cos	c	−cos β cos α.	(5.7)
	R

68

Формули п’яти елементiв

sin Ra cos γ = sin Rb cos Rc −cos Rb sin Rc cos α, sin Rb cos α = sin Rc cos Ra −cos Rc sin Ra cos β,

sin Rc cos β = sin Ra cos Rb −cos Ra sin Rb cos γ, sin α cos Rc = sin β cos γ + cos β sin γ cos Ra ,

sin β cos Ra = sin γ cos α+ cos γ sin α cos Rb , sin γ cos Rb = sin α cos β + cos α sin β cos Rc .

Формули для знаходження сферичного надлишку

ε

sin

a

sin

b

sin γ

sin

a

sin

c

sin β

sin

b

sin

c

sin α

2R

2R

2R

2R

2R

sin

=

2R

=

=

,

c

b

a

2

cos 2R

cos

cos 2R

2R

tg2

ε

= tg

p

·

tg

p−a

·

tg

p−b

·

tg

p−c

,

p =

a+ b + c

.

4

2

2

2

2

2

(5.8)

(5.9)

(5.10)

(5.11)

(5.12)

(5.13)

(5.14)

(5.15)

Розглянемо рiзнi випадки розв’язання сферичних трикутникiв.

1. Вiдомi положення вершин трикутника.

Нехай L1, L2, L3 — довготи, а ϕ1, ϕ2, ϕ3 — геоцентричнi широти вершин A, B, C сферичного трикутника (рис. 5.4).

Розглянемо одну з сторiн, скажiмо, AC . Проведемо з полюсу P сфери два меридiани, яким вiдповiдають довготи L1 та L3. З рис. 5.4 видно, що в сферичному трикутнику PAC вiдомi центральнi кути

AOP = π2 −ϕ1, COP = π2 −ϕ3.

та кут

APC = L3 −L1,

атому для знаходження центрального кута AOC скористаємось форму-

лами типу (5.2)–(5.4), виконавши пiдстановку

b

→

π

−ϕ1,

c

→

π

−ϕ3, α → L3 −L1,

R

2

R

2

отримаємо

cos( AOC)=cos

π

−ϕ1

cos

π

−ϕ3

+sin

π

−ϕ1

sin

π

−ϕ3

cos(L3 −L1)=

2

2

2

2

=sin ϕ1 sin ϕ3 +cos ϕ1 cos ϕ3 cos(L3 −L1) ≡ TAOC , (отриманий вираз позначено через TAOC ). Звiдси випливає

AOC = arccos(TAOC ).

69

		P
	L3 −L1
		b	C
A			γ
	α
	ϕ1	ϕ3	a
		O
		ϕ2
	c

β

B

Рис. 5.4. До знаходження сторiн сферичного трикутника

Аналогiчно для iнших двох центральних кутiв маємо

AOB = arccos(TAOB),	BOC = arccos(TBOC )
де позначено
TAOB = sin ϕ1 sin ϕ2 + cos ϕ1 cos ϕ2 cos(L2 −L1),

TBOC = sin ϕ2 sin ϕ3 + cos ϕ2 cos ϕ3 cos(L3 −L2). Довжини сторiн сферичного трикутника ABC дорiвнюють

a = R · BOC, b = R · AOC, c = R · AOB. Формули для знаходження кутiв наведено далi.

2. Вiдомi сторони трикутника.

Формули для знаходження кутiв мiж сторонами отримуються з спiввiд-

ношень (5.2)–(5.4):

!,

cos

a

−cos

b

cos

c

α = arccos

R

R

R

(5.16)

sin

b

sin

c

R

R

cos

b

−cos

c

cos

a

!,

β = arccos

R

R

R

(5.17)

sin

c

sin

a

R

R

70