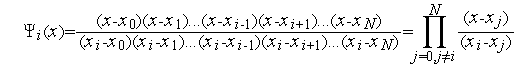Глава 5. Методы поиска глобального минимума одномерных многоэкстремальных функций

Метод перебора. Одномерный метод Монте-Карло

Некоторые методы решения многомерных задач оптимизации требуют решения одномерной задачи глобальной оптимизации (или совокупности таких задач).

Рассматривается следующая одномерная задача условной глобальной оптимизации): найти минимум, вообще говоря, многоэкстремальной функции (), определенной в замкнутойобласти допустимых значений ,

(1)

Метод перебора

Схема метода перебора (см. рис. 1):

Рис. 1.  К схеме метода перебора.

1. Покрываем интервал 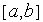некоторой сеткой с узлами,[1,].

2. Производим испытание в точке , т.е. вычисляем значенияфункциив этой точке.

3. Полагаем .

4. Производим испытание в точке - вычисляем значение() функции() в этой точке.

5. Если , то выполняем присваивания,.

6. Если , то выполняем присваивание1 и переходим на п.4). Иначе - заканчиваем вычисления.

7. Принимаем в качестве приближенного значения точки глобального минимума функции() на интервале [,] или каким-либо из рассмотренных одномерныхметодов локальной оптимизации организуем в окрестности точки поиск локального минимума этой функции

При выборе количества узлов сетки ,[1,] можно исходить из требуемой точности решения– максимальный шаг сетки принять равным этой величине.

Отметим, что метод перебора, как и любой другой метод глобальной оптимизации, при отсутствии априорной информации о свойствах минимизируемой функции не гарантирует нахождение глобального минимума (см. пунктирный график на рис. 1).

Одномерный метод Монте-Карло

Схема одномерного метода Монте-Карло:

1. Генерируем с помощью какого-либо программного генератора случайных чисел, равномерно распределенных в интервале [,], случайное число.

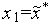2. Производим испытание в точке - вычисляем значенияфункции() в этой точке.

3. Полагаем 2.

4. Аналогично п. 1) генерируем случайное число [,] .

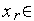5. Производим испытание в точке - вычисляем значение() функции() в этой точке.

6. Если , то выполняем присваивания,.

7. Если , то выполняем присваивание1 и переходим на п. 4). Иначе - заканчиваем вычисления. Здесь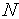– количествоиспытаний.

8. Принимаем в качестве приближенного значения точки глобального минимума функции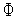() на интервале [,] или каким-либо из рассмотренных одномерныхметодов локальной оптимизации организуем в окрестности точки поиск локального минимума этой функции

При достаточно большом метода гарантирует нахождение глобального минимума с высокой вероятностью.

Метод выделения интервалов унимодальности

Рассмотрим одномерную задачу условной глобальной оптимизации): найти минимум одномерной многоэкстремальной функции (), определенной взамкнутой области допустимых значений и имеющей в этой области конечное число минимумов,

(1)

Метод выделения интервалов унимодальности функции () требует априорного знания оценки0 минимального расстояния между локальными минимумами этой функции.

Схема метода (см. рис. 1):

Рис. 1.  К схеме метода выделения интервалов унимодальности.

1. Полагаем =1.

2. Если функция () в точкевозрастает, то полагаемпереходим на п. 4).

3. Если функция () в точкеубывает, то полагаеми переходим на п. 5).

4. Последовательно увеличивая на величинупо формуле,, находим первую точку, в которой функция() убывает. Здесь и далее- величина в несколько раз меньшая величины.

5. Последовательно увеличивая 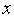на величинупо формуле,, находим первую точку, в которой функция() возрастает.

6. В качестве -го интервала унимодальности принимаем интервал [,].

7. Если интервал [,] исчерпан, переходим на п.8), иначе полагаем,и переходим на п.4).

8. Положим, что общее количество найденных интервалов унимодальности функции () равно-1. Каким-либо одномернымметодом локальной оптимизации находим локальный минимум функции () в каждом из-1 интервалов унимодальности. Обозначим точки этих минимумов. Соответствующие значения функции() обозначим,. Добавим к точкамточки,и вычислим соответствующие значения,функции().

9. Найдем минимальную из величин ,[0,] и соответствующее значение аргумента:.

10. В качестве решения задачи глобальной оптимизации (1) примем точку

На рис. 1 интервалами унимодальности являются интервалы [,], [,], [,].

Для определения того, возрастает или убывает в данной точке функция (), может использоваться ее первая разность в этой точке, где- некоторая малая величина. А именно, если>0, то функция возрастает в точке; иначе – убывает. Заметим, что при этом в каждой точке требуется выполнить дополнительноеиспытание функции ().

Если функция () непрерывно дифференцируема в интервале [,], то для определения того, возрастает или убывает в данной точке эта функция, можно, очевидно, использовать значения первой производной функции() в этой точке. А именно, если, то в точкефункция() возрастает; в противном случае – убывает.

Замечание 1. Если априорная оценка минимального расстояния между локальными минимумами функции() отсутствует, то никаких оснований полагать, что в интервалах, выделенных с помощью рассмотренного алгоритма, функция() являетсяунимодальной функцией. Пусть, например, функция () на интервале [,] постоянна (см. рис. 2). Если к такой функции применить алгоритм выделения интервалов унимодальности с любым>0, то в качестве интервала унимодальности будет выделен интервал, на котором функция() имеет бесконечное количество минимумов, т.е. не являетсяунимодальной функцией

Рис. 2.  К замечанию 1.

Метод аппроксимирующих моделей

Рассмотрим одномерную задачу условной глобальной оптимизации): найти минимум одномерной мультимодальной функции (), определенной в замкнутойобласти допустимых значений :

(1)

Схема метода

Схема метода аппроксимирующих моделей (см. рис. 1):

1. Покрываем интервал [,] некоторой сеткой с узламии производимиспытания в точках , т.е. вычисляем значения функции() в этих точках,.

2. Строим аппроксимирующую функцию (), проходящую через точки,. Эту функцию принято называтьматематической моделью минимизируемой функции () илимодельной функцией.

3. Оцениваем адекватность построенной модели 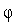(). Для этого:

• производим дополнительные испытания функции () в некоторых точках,;

• вычисляем значения модельной функции () и функции() в этих точках(),;

• вычисляем погрешность аппроксимации, например, .

Если погрешность аппроксимации превышает заданную, то по результатам всех предшествующих испытаний строим новую модельную функцию () и переходим на п. 3).

Определяем положение глобального минимума модельной функции (), который или принимается в качестве глобального минимума функции(), или уточняется с помощью какого-либометода локальной оптимизации

Рис. 1.  К схеме метода аппроксимирующих моделей. N=5;

На рис. 1 ,- точки локального минимумамодельной функции (); точка- приближенное значение точки глобального минимума функции() на интервале.

В качестве модельных функций () чаще всего используют полиномы и сплайны.

Рассмотрим использование в качестве модельной функции полиномов.

Аппроксимирующий полином Лагранжа

Будем искать аппроксимирующий полином в виде

(2)

где (),- неизвестные полиномы от, независящие от аппроксимируемой функции().

Из того условия, что модельная функция () должна совпадать с аппроксимируемой функцией() в узлах сетки,[0,], имеем систему изравенств

(3)

Для выполнения равенств (3) полиномы ,, очевидно, должны удовлетворять условиям

(4)

или, другими словами, полином (),должен иметь в качестве корней все числа,, кроме числа, а придолжен иметь значение, равное единице.

Условию (4) удовлетворяют только полиномы вида , где– неизвестная константа. Найдем эту константу из условия:

;

.

Таким образом,

(5)

и искомый аппроксимирующий полином определяют выражением

(6)

Полином (6) называется аппроксимирующим полиномом Лагранжа.

Использование аппроксимирующего полинома Лагранжа (6) в качестве модельной функции идейно очень просто, но обладает существенным недостатком. Пусть после построения этого полинома на сетке ,[0,] и проверке его адекватности выясняется, что погрешность аппроксимации превышает заданную. Тогда, в соответствии с рассмотренной выше схемой метода, необходимо построить новый полином Лагранжа на сетке, полученной объединением сеток,, что требует пересчета всех посчитанных ранее функций,. От этого недостатка свободна модификация аппроксимирующего полинома Лагранжа – аппроксимирующий полином Ньютона.

Нахождение стационарных точек аппроксимирующего полинома.

После построения аппроксимирующего полинома возникает задача нахождения стационарных точек функции () (см. схему метода). Поскольку аппроксимирующий полином непрерывен и, по крайней мере, один раз непрерывно дифференцируем, его стационарные точки удобно искать как нули первой производной – т.е. как корни уравнения

(7)

Для поиска корней уравнения чаще всего используют метод хорд и метод касательных, использующие линейную интерполяцию функции () (см. параграф 4.8), а также другие методы.