1. Постановка задачи.

Выполнить несколько итераций (не менее двух) решения двумерной задачи локальной безусловной оптимизации

(10)

(11)

градиентным методом с дроблением шага, исходя из точки .

Принять ,, в качестве нормы вектора градиента использовать евклидову норму.

Траекторию поиска изобразить на рис. 3, на котором приведены линии уровня квадратичной функции (11), полученные с помощью MATLAB-программы, приведенной в параграфе 6.1.

Рис. 3.  К примеру 1. Фрагмент (три итерации) траектории поиска минимума функции (11) градиентным методом с дроблением шага, исходя из точки X⁰=(x⁰,y⁰)=(-2.0,1.0).

2. Итерационная формула.

Итерация градиентного метода с дроблением шага для задачи (10), (11) имеет вид

(12)

(13)

а величина шага находится из условия

(14)

Найдем явные выражения для частных производных функции (11):

(15)

Таким образом, из (12), (13), (15) имеем искомую итерационную формулу градиентного метода с дроблением шага для задачи (10), (11).

=-,=-,

(16)

3.Первая итерация (=0).

Из формул (15), (16) последовательно имеем

Таким образом, (см. рис. 3).

Условие (14) на первой итерации имеет вид

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на первой итерации условие (14) выполняется и величина шага должна быть изменена:

4.Вторая итерация (=1).

Аналогично первой итерации последовательно имеем

Таким образом, (см. рис. 3).

Условие (14) на второй итерации имеет вид

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на второй итерации условие (14) выполняется и величина шага должна быть изменена:.

5.Третья итерация (=2).

Аналогично первой итерации последовательно имеем

Таким образом, (см. рис. 3).

Условие (14) на третьей итерации имеет вид

()-()0.5.

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на третьей итерации условие (14) выполняется и величина шага должна быть изменена:.

Градиентный метод с дроблением шага. Тест 1

Выполните несколько итераций (не менее двух) решения двумерной задачи локальной безусловной оптимизации

(1)

(2)

градиентным методом с дроблением шага, исходя из точки .

Примите ,, в качестве нормы вектора градиента используйте евклидову норму.

Траекторию поиска изобразите на рисунке, на котором приведены линии уровня квадратичной функции (2), которые могут быть получены с помощью следующей MATLAB-программы:

x=-2:0.06:2;

y=x;

[X,Y]=meshgrid(x);

Z=(X).^2+(Y).^2+3*(X+Y).^2;

V=[0.1,0.2,0.4,0.8,1.5,3.,6.,12,24];

[C,h]=contour(X,Y,Z,V);

clabel(C,h);

 Ответ 

Итерационная формула.

Итерация градиентного метода с дроблением шага для задачи (1), (2) имеет вид

(3)

(4)

а величина шага находится из условия

(5)

Найдем явные выражения для частных производных функции ():

(6)

Таким образом, из (3), (4), (6) имеем искомую итерационную формулу градиентного метода с дроблением шага для задачи (1), (2).

=-,=-,

(7)

Первая итерация (=0).

Из формул (6), (7) последовательно имеем

Таким образом, (см. рис. 1).

Условие (5) на первой итерации имеет вид

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на первой итерации условие (5) выполняется и величина шага должна быть изменена:

Вторая итерация (=1).

Аналогично первой итерации последовательно имеем

Таким образом, (см. рис. 1).

Условие (5) на второй итерации имеет вид

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на второй итерации условие (5) выполняется и величина шага должна быть изменена:.

Третья итерация (=2).

Аналогично первой итерации последовательно имеем

Таким образом, (см. рис. 1).

Условие (5) на третьей итерации имеет вид

()-()0.5.

Поскольку

левая часть этого неравенства равна . Его правая часть, легко видеть, равна.

Таким образом, на третьей итерации условие (5) выполняется и величина шага должна быть изменена:.

Рис. 1.  Фрагмент (три итерации) траектории поиска минимума функции (2) градиентным методом с дроблением шага, исходя из точки X⁰=(x⁰,y⁰)=(-2.0,1.0).

Метод оптимизации Ньютона

Положим, что функция () всюду дважды дифференцируема в-мерном евклидовом пространстве.

Рассмотрим следующую многомерную задачу локальной безусловной оптимизации: найти минимум критерия оптимальности (), определенного в-мерном евклидовом пространстве,

(1)

Обоснование метода оптимизации Ньютона.

Рассмотрим первые три члена разложения функции () в ряд Тейлора в окрестности точки:

(2)

Здесь () -матрица Гессе функции (). Из (2) следует, что градиент функции() равен

(3)

Если матрица Гессе () положительно определена, то функция() достигает минимума в точке, в которой градиент этой функции равен нулевому вектору.

Таким образом, в точке минимума функции() справедливо равенство

(4)

где --мерный вектор нулей. Отсюда получаем итерационную формулу

(5)

для отыскания очередного приближения к точке минимума функции (). Здесь

(6)

Выражение (5) представляет собой итерационную формулу решения системы уравнений (4) широко известным методом касательных (методом Ньютона) – см. параграф 4.8. Этим фактом объясняется название рассматриваемого метода оптимизации.

Найдем скалярное произведение градиента функции () в точкеи вектора:

(7)

Последнее неравенство справедливо в силу постулируемой положительной определенности матрицы Гессе в точке . Геометрически неравенство (7) означает, что векторобразует тупой угол с градиентомцелевой функции () в точке(см. рис. 1). Таким образом, при минимизацииовражных функций вектор может составлять с осью оврага меньший угол, чем вектор антиградиента. Эта особенность делаетметод оптимизации Ньютона, вообще говоря, более эффективным, чем градиентный метод наискорейшего спуска.

Рис. 1.  К обоснованию метода многомерной оптимизации Ньютона.

Отметим трудности, которые могут возникать при использовании итерационной формулы (5):

• Если размерность пространства велика, то обращение на каждой итерацииматрицы Гессе () может потребовать значительных вычислительных ресурсов;

• Значение минимизируемой функции () в точке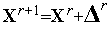может превышать значение функции в предыдущей точкевследствие того, что направлениеведет к уменьшению(), но величина шага слишком велика;

• Направление спуска, определяемое вектором , ведет к убываниюцелевой функции только при положительной определенности матрицы Гессе (). Это приводит к тому, что на каждой итерации необходимы вычислительные затраты на проверку обусловленности этой матрицы. Указанная матрица может быть плохо обусловленной. Более того, указанная матрица может быть вырожденной и, поэтому, не иметь обратной матрицы.

Вследствие этих трудностей итерационная формула (5) в «чистом» виде не используется в вычислительной практике.

Для того чтобы избежать обращения матрицы Гессе, на практике вектор находят обычно из следующей системы линейных алгебраических уравнений (СЛАУ), вытекающей из равенства (6):

(8)

СЛАУ (8) может быть решена различными численными методами (например, прямыми методами, итерационными методами).

Величина шага в направлении , которая приводит к убыванию функции(), может быть обеспечена путем добавления в итерационную формулу (5) коэффициента, т.е. путем использования вместо формулы (5) итерационной формулы

(9)

где коэффициент выбирают тем или иным способом так, чтобы обеспечить условие.

Для того, чтобы направление спуска независимо от определенности матрицы Гессе () вело у убыванию функции(), в качестве вектораможно использовать вектор

(10)

где --единичная матрица, а- параметр, выбираемый так, чтобы матрицаявлялась положительно определенной.

Схема метода оптимизации Ньютона.

Рассмотрим схему одной из модификаций метода оптимизации Ньютона, в которой используется итерационная формула (9) и вектор находят путем решения на каждой итерации СЛАУ (8).

1. Задаем начальную точку , начальную величину шагаи коэффициент дробления шагаПолагаем счетчик числа итераций=0.

2. Вычисляем в точке вектор градиента() иматрицу Гессе ().

3. Решаем СЛАУ (8) и находим вектор .

4. По формуле (9) вычисляем компоненты вектора .

5. Вычисляем величину 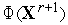- значение функции() в точке.

6. Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем , и завершаем итерации. Иначе – переходим к следующему пункту.

7. Если <, то полагаем=+1 и переходим к п.2. Иначе – фиксированное число раз полагаеми переходим к пункту 4

В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:

или условие

где - константа, определяющая требуемую точность решения по градиенту функции().