Представление графов

Наиб извест и попул способ представл графов состоит в геометр изображении.

Матрица смежности ориентир помеченного графа с n вершин наз матрица А={}, lj=1…n

Способы задания графов

В большинстве случаев граф задается с помощью матриц.

1. Матрица смежности вершин – это матрица порядка , где n –

число вершин. Ее строки и столбцы соответствуют вершинам графа. Элемент

pij матрицы смежности равен числу дуг, идущих из i-ой вершины в j-ю. Если

граф не имеет параллельных дуг, то матрица будет состоять только из 0 и 1.

Матрица смежности вершин однозначно определяет структуру

графа.

Матрица смежности вершин

Аналогично можно определить матрицу смежности дуг. Это матрица порядка , где m – число дуг. Элемент матрицы равен 1, если дуга ui непосредственно предшествует дуге uj.1. Матрица инциденций – это матрица размерности , где n – число

вершин, m – число дуг. Элементы rij этой матрицы равны +1, если дуга ui исходит из i – ой вершины, +1, если дуга входит в i – ю вершину, 0 – если дуга не инцидентна i-ой вершине. В случае неориентированного графа элементом матрицы будет 1, если дуга

инцидентна вершине и 0 в противном случае.

3. Двудольные графы. Планарные графы.

Условия существования двудольных графов. Алгоритм определения максимального

паросочетания. Хроматические графы. Паросочетания. Радиус, центр и диаметр графа.

Деревья. Остовные деревья. Алгоритм ближайшего соседа, жадный алгоритм построения

минимального остовного дерева. Непланарность графа К5 и графа К3,3 .

Граф Г=(X,U,Ф) наз двудольным, если мн-во его вершин можно разбить на 2 незав подмнва , таких, что . Такой граф будем обозначать как

Условие существования двудольных графов.

Теорема:

Граф Г=(X,U,Ф) явся двудолным ТИТТК любой его простой цикл четной длины.

Паросочетанием в двудольном графе назся независимое подмнво ребер , ребра не имеют общих вершин.

Паросочетание наз макс, если любое другое паросочетание содержит меньшее число ребер.

Теорема о максимальном паросочетании

Пусть - двудольный граф. Тогда количество ребер в максимальном паросочетании равно , где

Хроматические графы

Пусть Г=(X,U,Ф)- простой граф. Граф Г- наз раскрашиваемым, если существует такое разложение множества его вершин на к непересекающихся подмножеств(компонент) таких, что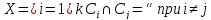 (1) и вершины в каждой компоненте независимы, т. Е. ребра в Г соединяют вершины только из разных компонент.

представление (1) наз к-раскраской графа Г. Вершины этого графа можно раскрасить к красками так, чтобы смежные вершины всегда были окрашены в разные цвета. Для этого достаточно вершины каждой компоненты покрасить своей краской.

Наименьшее возможное числокомпонент в разложении (1) наз хроматическим числом графа Г.

Утверждение Полный граф Г=(X,U,Ф) на вершинах имеет хроматическое число . здесь каждая компонента разложения (1)состоит из одной вершины

Утверждение граф Г=(X,U,Ф) содержит максимальный подграф (клику) из к вершин ТИТТК его хроматическое число равно к или к+1.

Утверждение граф Г=(X,U,Ф) явлся двудольным ТИТТК

Утверждение хроматическое число дерева равно 2, так как дерево явся двудольным графом.

Диаметр, радиус и центры графа

Пусть Г=(X,U,Ф)-конечный связный псевдограф. Обозначим через d=(x,y)длину минимального маршрута между вершинами x,yєX.

Величина наз диаметром графа.

Пусть -произвольная вершина графа. Величина назся максимальным удалением в графе Г от вершины х.

Радиусом графа Г назся величина

Любая вершина zєX, для которой r(z)=r(Г), назся центром графа.

Деревом называется связный граф, не содержащий циклов

Любой граф без циклов называется лесом. Таким образом, деревья являются

компонентами леса.

Пусть G=<V,U>, V – конечное множество вершин, U – конечное

множество ребер, .

Свойства деревьев

1. G – связный граф и m=n-1.

2. G – ациклический граф.

3. Любые две несовпадающие вершины G соединяет единственная

простая цепь.

4. Если какую-то пару несмежных вершин G соединить ребром, то

полученный граф будет содержать ровно один цикл.

Ориентированный граф называется ориентированным деревом, если:

1. Существует ровно одна вершина называемая корнем, которая не

имеет предшествующих вершин.

2. Любой вершине в графе G непосредственно предшествует

ровно одна вершина.

Неориентированное дерево можно превратить в ориентированное

дерево, выбрав в качестве корня произвольную вершину. На рис. 42 корень

графа – вершина v6.

Теорема Кэли. Число разных деревьев, которые можно построить на n

вершинах равно .

Пусть G=<V,U> - граф. Остовной подграф – это подграф,

содержащий все вершины. Остовной подграф, являющийся деревом

называется остовом.

Теорема. Число ребер произвольного неориентированного графа G,

который надо удалить для получения остова, не зависит от

последовательности их удаления и равно m-n+k, где m – число ребер, n –

число вершин и k – число компонент связности графа.

Минимальный остов графа

Дан взвешенный граф

Найти остов минимального веса (экстремальное дерево). Найти матрицу фундаменталь-

ных циклов графа относительно этого остова.

Решение

Построение остова минимального веса

Способ 1. Алгоритм Дж. Краскала [5], с.60.

Строим граф, присоединяя к пустому графу на множестве вершин заданного графа ребро наи-

меньшего веса. К полученному графу последовательно присоединяем остальные ребра, выбирая на

каждом шаге ребро наименьшего веса, не образующее цикл с имеющимися ребрами.

В нашем случае начинаем с ребра весом 13 – наименьшего в графе. На рисунках дана последо-

вательность действий. Ребро весом 19 не включается в остов, так как оно образует цикл с ребрами

весом 14 и 13.

Способ 2. Алгоритм ближайшего соседа[6], с.145.

Алгоритм Дж. Краскала требует на каждом шаге проверки на цикличности предварительной

сортировки ребер по весам, что затруднительно для графов с большим числом ребер. Несколько

20проще следующий алгоритм.

1. Отмечаем произвольную вершину графа, с какой начнется построение. Строим ребро наи-

меньшего веса, инцидентное этой вершине.

2. Ищем ребро минимального веса инцидентное одной их двух полученных вершин. В множе-

ство поиска не входит построенное ребро.

3. Продолжаем далее, разыскивая каждый раз ребро наименьшего веса, инцидентное построен-

ным вершинам, не включая в круг поиска все ребра, их соединяющие.

В нашем примере начнем с вершины A. На рисунках дана последовательность действий

Теорема (Непланарность ):

Граф  непланарен.

Доказательство:

Граф  имеет 5 вершин и 10 ребер. Если он планарен, то по следствию из формулы Эйлера получаем . Что невозможно.

Теорема (Непланарность ):

Граф  непланарен.

Доказательство:

Граф  содержит ,  и  граней. 

Пусть граф  планарен. Тогда по формуле Эйлера . Пусть, двигаясь вдоль -й грани мы пройдем  ребер. Очевидно, что . Поскольку граф двудольный, все его циклы имеют четную длину. Значит . Получаем , то есть . То есть , что невозможно.