11 ALGEBRA

5. The Mean Value Theorem

MEAN VALUE THEOREM

Let f: [a, b] R be a continuous function. Then there exists at least one real number c [a, b] such that

b

f (x) dx

f (c)=	a		.
		b a

In the given formula, f(c) is called the mean value of f(x) on the interval [a, b].

EXAMPLE 69 Find the mean value of f(x) = x2 – 4x on the interval [0, 4].

Solution Let f(c) be the mean value of f(x) in [0, 4].

By the Mean Value Theorem we have

4
	(x2				4x)dx
f (c)=	0
				4 0
			3		2		4
( x				4 x
							)|
=		3			2		0
					4
64					64
=	3				2
				4

= 83.

Check Yourself 12

				x			F (3 ).
1.	Given F(x)= sint3 dt, find
				2			3
				x3
2.	Given F(x)= (t2 +4t 1) dt, find F (3).
				x2
3.	Find the mean value of f (x)=							x3 +2x2 +1	on the interval [1, 3].
								x2
Answers
1.		3	2.	21876	3.	13
	2					3

Integrals

49

B. INTEGRALS OF SOME SPECIAL FUNCTIONS (OPTIONAL)

1. Integrating Absolute Value Functions

Recall that an absolute value function |f(x)| is a function such that

	f (x),	f (x) 0
f (x)
	=
	f (x), f (x) <0.

When integrating absolute value functions, first we find the positive and negative parts of given function. For the intervals where f(x) changes its sign we use the fifth property of

definite integrals:	c	b	c
for a b c,	f (x) dx = f (x) dx+ f (x) dx.
	a	a	b

	70	2
EXAMPLE		| x| dx =?
		3
			x if x 0
Solution		|x| =																	y
		x if x		0															y = |x|
		2	0				2				2	0				2		2
		So | x| dx = ( x) dx+ x dx = x										| + x					|
		3	–3				0			2		3			2			0	x
				02		( 3)2			22			02		=	13			–3	2
			=	2		2			2			2			2			.

	71	3
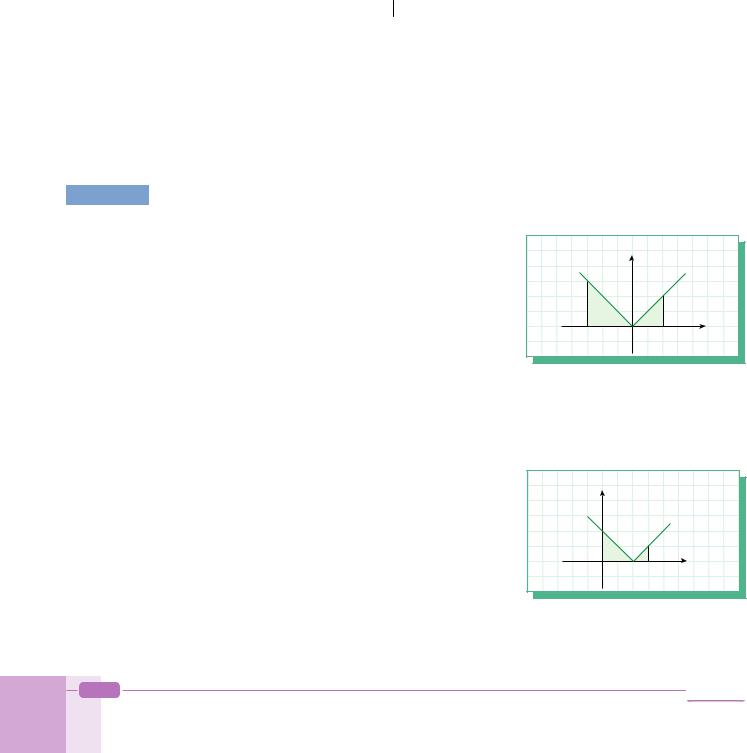
EXAMPLE				x 2				dx =?
		0
Solution		x – 2 = 0								x = 2 is the root of x – 2.
										(x 2)	if x 2
		So f(x)=
										x 2	if x 2.
		3							2					3
		So				x 2				dx = (x 2) dx+ (x 2) dx
		0							0					2
											x2		2	x2	3
										=	2	+2x |+			2x |
													0	2	2
										= 2+4+ 9			6	2+4 = 5.
												2			2

y

y = |x – 2|

x

2 3

50	Algebra 11

	72	3
EXAMPLE		| x2 1| dx =?
		3

Solution If x2 – 1 = 0, then x = 1 or x = –1.

	x2	1,	x 1 or x –1
	|x2 – 1| =
	1 x2 ,		1 x 1
3	1		1			3
| x2 1| dx = (x2 1) dx+ (1 x2 ) dx+ (x2 1) dx
3	3		1			1
	3		3		3	x)|= 44.
	=( x	x)|+(x x		)|+( x
		1		1		3
	3	3	3	1 3		1 3

yy = |x2 – 1|

x

–3 –1 1 3

	73
EXAMPLE		|cos x| dx =?
		0

Solution		cos x	on	[0,				y
							]
|cos x| =							2			y = |cosx|
								1
			on	[		,	]
	cos x				2
								p	p	x
								2
	2
|cos x| dx = cos x dx+ cos x dx
0	0
			2

2
= (sin x | ) + (–sin x | )
		2

=(sin 2 sin0)+( sin +sin 2)=1+1.

Check Yourself 13

Evaluate the definite integral of each absolute value function.

2			4
a. | x+1| dx			b. | x2	3x+2| dx			c. |sin x| dx
2			2
3			3				4
d.	x2 2x+1 dx		e. | x2 x| dx				f. | x2 9| dx
1			1				3
Answers
a. 5	b. 55	c. 4	d. 4	e.	17	f.	118
	3				3		3

Integrals

51

2. Integratign Sign Functions

Recall the definition of the sign function:

	1 ,	f(x) 0
	0 ,	f(x) 0 .
sgn f x
	1,	f(x) 0

When integrating a sign function, we divide the interval into two parts as negative and positive intervals, since f(x) is not continuous at the point where f(x) = 0

	74	1
EXAMPLE		sgn(x+1) dx =?
		2

Solution	x + 1 = 0	x = –1					y
		1			x –1		1
	sgn(x+1)=		0		x= –1
						–2
								x
			1		x –1	–1	1
	1			1	1		–1
	sgn(x 1) dx=				1 dx+ 1 dx
	2			2	1

1	1
= x |+ x |
2	1

=1– 2+1– (–1)

		=1.
	75	4
EXAMPLE		sgn(x2 4) dx =?
		3

Solution	x2 – 4 = 0	x = 2							y
			1		x 2 or x 2				1
	sgn(x2 – 4)=				x = 2
			0					–2	2	x
							–3
										4
			1		2 x 2
	4			2	2	4			–1
	sgn(x2 4) dx=			dx+		dx+ dx
	3			3	2	2

2	2	4
x |+( x) |+ x|
3	2	2

(–2) – (–3)+(–2) 2+4 – 2

= –1.

52	Algebra 11

3. Integrating Floor Functions

The floor function f(x) is the greatest integer value which is not greater than f(x). If f(x) Z then f(x) is not continuous. For the points of discontinuity (i.e. for critical points) there is no integral. For this reason, when integrating a floor function we divide the interval into subintervals by using discontinuity points.

	76	3
EXAMPLE		x 1 dx =?
		1	y
Solution		Look at the graph of x 1 .	1
		For 1 x 0, x 1 = 2.	1
		–1		x
		For 0 x 1, x 1 = 1.
			2	3
		For 1 x 2, x 1 0.	–1
		For 2 x 3, x 1 =1.	–2

3	0	1	2	3
So	x 1 dx = 2 dx+ 1 dx+ 0 dx+ dx
1	1	0	1	2
	0	1	3
	= 2x |+( x)|+0+ x|
	1	0	2

=0 – 2+(–1) – 0+3 – 2

=–2.

Check Yourself 14

Evaluate the integrals.

		2		4				3
1.	a.	sgn x dx	b.	sgn(x 3) dx			c.	|sgn(x2	1)| dx
	1			3				2
		2		3	x			2
2.	a.	x 1 dx	b.			dx	c.	sgn x dx
	2			1	2			1
Answers
1.	a. 1	b. –5 c. 5	2. a. –6 b. 0 c. 0

Integrals

53

APPLICATIONS IN PHYSICS

acceleration (a)

velocity

time (t)

velocity (v)

displacement

time (t)

Integrals have many applications in physics. In fact, some people say that calculus developed because of physics. Newton, one of the fathers of calculus, was also a great physicist.

How can we use integrals in physics? Let us look at some applications.

The area under a velocity-time graph gives us the displacement of a moving object. Also, the area under an acceleration-time graph is the velocity of the object. So we can say that the integral of the function of acceleration is velocity, and the integral of the function of velocity is distance or displacement.

We know that the gravity of acceleration of the earth (g) is about 9.8 m/s2. Therefore, when you drop an object from a height, its speed after t

seconds will be a(t) dt where a(t) is the acceleration of the earth, g.

After integrating this function we get:

velocity = a(t) dt = g dt = g t +c = 9.8 t+ c .

How can we calculate the constant c? For this, we use information about the velocity. If we throw an object with a speed v0 then at time t = 0 the velocity will be v0. Substituting this information in the equation gives us:

v = 9.8 t + c

v0 = 9.8 0 + c = c.

So we have the equation:

velocity = acceleration time + initial velocity .

If we integrate this velocity function with respect to time then we get the distance:

Distance = v(t) dt.

Again by using the given information we can find c from the initial height. Let us look at two examples of using these formulas.

	1 A rocket is launched. Its initial velocity is 120 m/s.
Example
	a. What is the velocity of the rocket after five seconds?
	b. What is the height of the rocket after five seconds?
	c. What is its maximum height?

Solution We can begin by writing v0 = 120 m/s, g = 9.8 m/s2. The rocket moves upward but the acceleration of gravity works downward, so we will take the acceleration of the rocket as negative: g = –9.8 m/s2. Now,

a.v(t) = g dt = –g t + c1

v(0) = –g 0 + c1. This means c1 = v0 = 120 m/s.

So the velocity at time t = 5 is v(5) = –9.8 5 + 120 = 120 – 49 = 71 m/s.

b.Let d(t) be the distance after time t.

Then d(t)= (–9.8 t+120) dt= – 21 9.8 t2 +120t+ c2.

We assume that the initial distance of the rocket is 0 m. Therefore when t = 0 we have

d(0)= 21 9.8 02 +120 0+ c2 = 0.

This gives us c2 = 0, which means d(t) = – 21 9.8 t2 + 120 t.

So we have d(5) = – 21 9.8 52 + 120 5 = 477.5 m.

c.At the rocket’s maximum height its velocity will be 0 m/s. Using the formula from part a we get v(t) = –9.8 t + 120 0 = –9.8 t + 120. This gives t 12.24.

So the maximum height = d(12.24) 734.7 m.

	2 A stone is dropped from a balloon.
Example
	a. What is the velocity of the stone after ten seconds?
	b. If the stone hits the ground after twenty seconds, what is the
	height of the balloon?

Solution a. Given information: g = 9.8 m/s2, v0 = 0,

v(t) = g dt = g t + c1.

When t = 0, v0 = 0 so c1 = 0. Using v(t) = g t after ten seconds:

v(10) = 9.8 10 = 98 m/s.

	b.	d(t)= 9.8 t dt =	1	9.8 t2 + c2 m.	The initial distance is assumed to be 0 so c2 = 0.
			2
						1	9.8 202 = 1960 m.
	So the height of the balloon = d(20) =
						2

EXERCISES 1.2

A.Evaluating Definite Integrals

1.Evaluate the area between the graph of f(x) = x and the x-axis on the interval [0, 3].

2.Find the integral of the function f(x) = 3x – 2 on the interval [0, 4] and find the area between the graph of f(x) and the the x-axis on the same interval.

3.In the figure, A = 5 cm2, B = 4 cm2 and C = 7 cm2. Find the area of the shaded region and evaluate the integral of f(x) on the interval [a, b].

4.Evaluate the integrals.

3

a. x2 dx

y

y = f(x)

AC

a	B	b	x

5

b. 3x dx

		2				1
		4
	c.	x3	dx			d. cos x dx
		0				0
		4		1		a
	e. ( x +				) dx	f. (ax2 +a2x) dx
				x
		1				0
		7
	g.		x 9 dx
		0

5. Evaluate the integrals.

4

a. 3x2 dx

3

4

b. (5x3 +4x2 +3x 5) dx

3

c. (sin3x+4cos2x) dx

0

5	3
6. f (x) dx = 7 is given. Evaluate	f (x) dx.
3	5

5 5

7. f (x) dx 5 and f (x) dx = 8 are given. Evaluate

1 3

3

f (x) dx.

1

	x	dF .
8. a. Given	F(x)= cos t dt, find
	1	dx
	1		dF .
b. Given	F(x)= (t2 +2t) dt,	find
	1/ x		dx

2		dF .
c. F(x)= x sint dt	is given. Find
0		dx
3			dF .
d. F(x)= x (x 4) dx is given. Find
x			dx

9. Find the mean value of each function on the given interval.

a. f(x) = x + 1 on [0, 5] b. f(x) = x3 + 1 on [–1, 2]

c. f (x)= x2 +2x+4 on [–3, 3] x

d. f(x) = sinx on [0, 2 ]

56	Algebra 11

B.Integras of Some Special Functions (Optional)

1.Integrate the absolute value functions.

2

a. | x 1| dx

3

5

b. | x+3| dx

5

	3
c.	|2x+3| dx
	2
	5
d.	| x2	1| dx
	2
	5
e.	| x2	3x 4|
	3
	5
f.	| x2 +3x+2| dx
	4
g.	|sin x| dx
	0
	2
h.	| x3 | dx
	1
	4
i.	x2 +6x+9 dx
	4

2. Integrate the sign functions.

7

a. sgn(x2 1) dx

3

2

b. sgn(x+1) dx

2

5

c. sgn(x2 2x+3) dx

3

4

d. sgn(x3 3x2 18x+40) dx

3

3

e. |sgn x | dx

2

0

f. sgn(x2 5x 6) dx

1

3. Integrate the floor functions.

2

a. x+1 dx

0

2

b. 2x 1 dx

1

2

c. x x+2 dx

1

3 x

d.0 2 dx

3

e. 3x dx

1

2 x

f.| x| x 2 dx

2

2

g. |sgn 1 x | dx

2

3

h. x 2x+5 dx

2

Integrals

57

A. FINDING THE AREA UNDER A CURVE

Definite integrals have many applications. We can use definite integrals to find the area of a region bounded by a curve, the volume created by rotating a curve, the length of a curve, the mean value of a function, the center of mass of an object, and to calculate the displacement and work done in motion and projectile problems.

Most of these applications are useful in mathematics or physics. In this chapter we will look at the applications of the definite integral in mathematics.

FINDING AREA

Let f: [a, b] R be a continuous function such that for	y			f(x)
every x, f(x) 0. Then the area of the region between
y = f(x) and the x-axis on the interval [a, b] is
b			A
A = f (x) dx.
					x
a		a	b

Conclusions

The theorem above gives us four important results.

1.If f(x) 0 then the area of the region between y = f(x) and the x-axis on the interval [a, b]

will be

b	b
A = f (x) dx = – f(x) dx.
a	a

y
a	b	x
	A
	f(x)

More generally, if y = f(x) is any continuous function on the interval [a, b] then the area between y = f(x) and the x-axis is

b

A = | f (x)| dx.

a

2.	In the figure, the total area of the region will be			y
	b	c	d					f(x)
	Area=A+B+C = f (x) dx f (x) dx+ f (x) dx.
					A
	a	b	c					C
									x
				a	b	B	c	d

58	Algebra 11