1 Шаг. Определение переменных.

Обозначим эти объемы как переменные модели:

x₁ — ежедневный объем производства краски для наружных работ;

х₂ — ежедневный объем производства краски для внутренних работ.

2 Шаг. Построение целевой функции.

Обозначим эту функцию через z (она измеряется в тысячах ден. ед.) и положим, что

z = 5x₁ + 4x₂.

В соответствии с целями компании получаем задачу:

максимизировать z = 5x₁ + 4x₂.

3 Шаг. Определение ограничений (условий).

Условия должны учитывать ограниченные возможности ежедневного потребления сырья и ограниченность спроса на готовую продукцию. Другими словами, ограничения на сырье можно записать следующим образом:

используемый объем сырья максимально возможный

для производства обоих ≤ ежедневный расход сырья

видов краски

6x₁ + 4х₂ ≤ 24 ограничение по использованию сырья М1

x₁ + 2x₂ ≤ 6 ограничение по использованию сырья М2

х₂ ≤ 2 максимальный объем производства краски для внутренних работ

х₂ – x₁ ≤ 1 ежедневный объем производства краски для внутренних работ не должна превышать ежедневный объем производства краски для наружных работ более чем на 1т.

х₁ ≥ 0, х₂ ≥ 0 ещё одно неявное ограничение состоит в том, что переменные x₁ и х₂ должны быть неотрицательными (условия неотрицательности).

Окончательно задача будет записана следующим образом (удобно переписать поставив на первую позицию переменную х1, на вторую – х2):

z = 5х₁ + 4х₂ → max

при выполнении следующих ограничений:

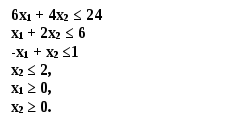
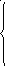
Этап решения модели

Задача сформулирована, теперь встает вопрос о нахождении оптимального допустимого решения, доставляющего максимум целевой функции. Можно сделать вывод, что задача имеет много (фактически, бесконечно много) допустимых решений. По этой причине невозможна подстановка значений переменных для поиска оптимума, т.е. нельзя применить простой перебор всех допустимых решений. Следовательно, необходима эффективная процедура отбора допустимых решений для поиска оптимального.

Существуют два наиболее распространенных способа решения задач линейного программирования (ЗЛП): графический метод и симплекс-метод. Графический метод существенно нагляднее и обычно проще для понимания и решения (хотя занимает много времени, так как требует тщательного построения чертежа).

Замечание. Графический̆ метод применим в случае двух переменных. Практических приложений у этого метода немного, но он важен для наглядности и понимания происходящего.

Сначала необходимо построить пространство решений, то есть получить область, точки которой удовлетворяют всем ограничениям. Каждое ограничение задает полуплоскость ограниченную некоторой̆ прямой, пересечение этих полуплоскостей̆ есть пространство решений.

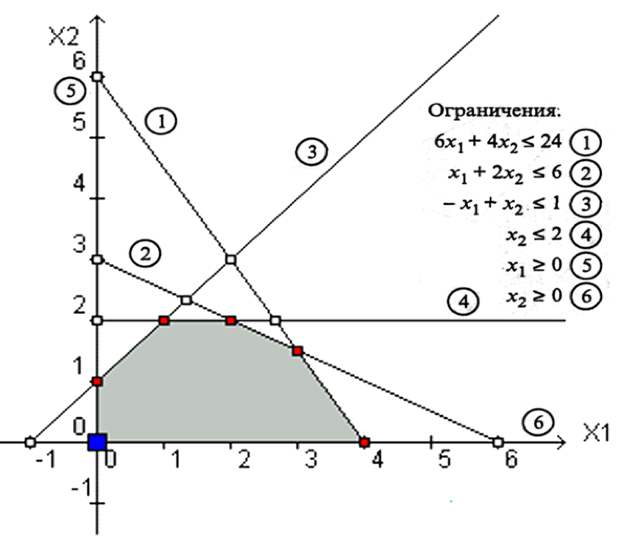
Далее, необходимо максимизировать z = 5x₁+4x₂. Рассмотрим семейство соответствующих прямых.

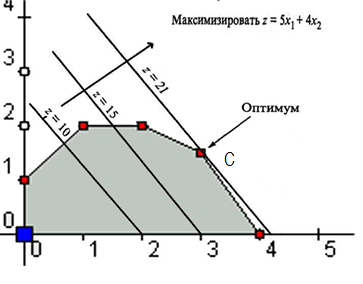
Если z=0, то 0 = 5х₁ + 4х₂ (0; 0) и (2; -2,5)_.

Если z=10, то 10 = 5х₁ + 4х₂ (0; 2,5) и (2; 0)_. Бесконечно много допустимых решений.

Если z=15, то 15 = 5х₁ + 4х₂ (0; 3,7) и (3; 0)_. Бесконечно много допустимых решений.

Направление возрастания функции z = 5х₁+4х₂ есть перпендикуляр к прямым соответствующего семейства. В следствии чего, мы можем увеличивать значение целевой функции, пока соответствующая ей прямая имеет хотя бы одну общую точку с пространством решений.

..\Book1.xls

В нашем случае оптимальное решение соответствует точке пересечения прямых x₁ + 2х₂ ≤ 6 и x₁ + 2х₂ ≤ 6, то есть в точке С(3; 1,5), а значение целевой функции 21.

Значит лучшим решением будет выпускать 3т и 1,5т, получая при этом прибыль в 21 тис. ден. ед.

Замечание (Об угловой точке) Очевидно, что если область задана произвольным многоугольником, а максимизируемая функция имеет общий̆ вид z = ax + by, то решение (оптимум) все равно будет достигаться в угловой̆ точке.

Если мы изменим угол наклона, то есть коэффициенты целевой функции, то увидим, что решение достигается в любом случае в одной из угловых точек (или в нескольких).

Решение задачи линейного программирования графическим методом включает следующие этапы:

1. На плоскости X₁0X₂ строят прямые.

2. Определяются полуплоскости.

3. Определяют многоугольник решений;

4. Строят вектор N(c₁; c₂), который указывает направление целевой функции;

5. Передвигают прямую целевую функцию c₁x₂ + c₂x₂ = z в направлении вектора N до крайней точки многоугольника решений.

6. Вычисляют координаты точки и значение целевой функции в этой точке.

Приведем основные свойства задачи ЛП.

1. Допустимое множество решений задачи ЛП либо пусто, либо является выпуклым многогранником в Rⁿ (как пересечение полупространств, описываемых ограничениями-неравенствами). Оно может быть, как ограниченным, так и неограниченным; в любом случае это замкнутый многогранник.

2. Если допустимое множество не пусто, а целевая функция ограничена сверху (для задачи максимизации, а для задачи минимизации - ограничена снизу) на этом множестве, то задача ЛП имеет оптимальное решение.

3. Оптимальные решения задачи ЛП (если они существуют) всегда находятся на границе допустимого множества. Точнее, если существует единственное оптимальное решение, то им является какая-либо вершина многогранника допустимых решений; если две или несколько вершин являются оптимальными решениями, то любая также является оптимальным решением (т.е. существует бесконечно много точек максимума или минимума).