|
Оператор
набла (оператор Гамильтона) ∇
– это символический вектор, сочетающий
в себе векторные и дифференцирующие
свойства. Поэтому при действии с
оператором ∇
необходимо применять правила векторной
алгебры.
В
декартовой системе координат оператор
∇
записывается:
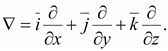
Существует
запись его в цилиндрической и сферической
системах координат.
При
оперировании со сложными функциями
используют правила дифференцирования
сложных функций:
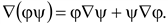 (14.5) (14.5)
Использование
оператора ∇
позволяет упростить запись некоторых
векторных операций. Так умножение
оператора ∇
на скалярную функцию означает градиент
этой функции
 .(14.6) .(14.6)
Скалярное
умножение ∇
и вектора приводит к дивергенции
вектора
 .(14.7) .(14.7)
Векторное
произведение ∇
на вектор дает ротор вектора
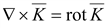 .(14.8) .(14.8)
Оператор
Лапласа
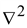 (лапласиан)
– это скалярный дифференциальный
оператор, определяемый как дивергенция
градиента скалярной функции (уравнение
Лапласа (лапласиан)
– это скалярный дифференциальный
оператор, определяемый как дивергенция
градиента скалярной функции (уравнение
Лапласа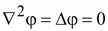 ). ).
В
декартовой системе координат оператор
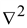 запишется: запишется:
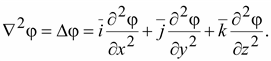 (14.9) (14.9)
Если
применить оператор
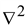 к
вектору к
вектору
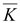 ,
то ,
то
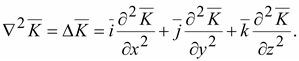 (14.10) (14.10)
где

Векторное
уравнение
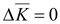 можно
представить тремя скалярными
уравнениями: можно
представить тремя скалярными
уравнениями:
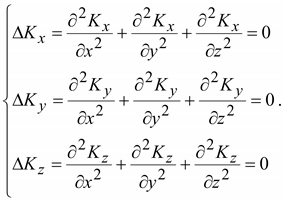 (14.11) (14.11)
|
Понятие
о градиенте, дивергенции и роторе
|
|
Градиент
скалярной функции – это вектор,
указывающий направление наиболее
быстрого возрастания скалярной
функции и по абсолютному значению
равный наибольшей скорости возрастания
этой функции.
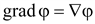 (14.12) (14.12)
Градиент
направлен по нормали к поверхности
равного уровня скалярной функции в
данной точке. Градиент скалярного
потенциала φ постоянного во времени
поля равен:
 (14.13) (14.13)
где
 –
нормаль к эквипотенциальной
поверхности в данной точке поля. –
нормаль к эквипотенциальной
поверхности в данной точке поля.
Градиент
скалярного потенциала φ в каждой
точке совпадает с касательной к
силовой линии напряженности
электрического поля
 в
данной точке и имеет направление,
противоположное вектору в
данной точке и имеет направление,
противоположное вектору
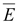 (рис.
14.3). (рис.
14.3).
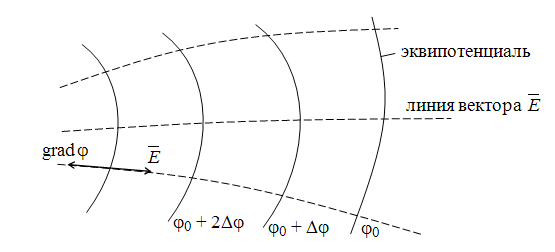
Рис.
14.3. Картина электрического поля
Дивергенция
(расхождение вектора) – это
алгебраическая скалярная величина,
характеризующая источники поля в
рассматриваемой точке поля или
указывающая на отсутствие источников
 . .
Численно
дивергенцию в данной точке определяют
как предел, к которому стремится
отношение потока вектора через
замкнутую поверхность к объему,
ограниченному этой поверхностью,
при стремлении этого объема к нулю
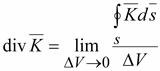 .(14.14) .(14.14)
Если
div
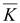 >
0, то имеются источники поля и линии
вектора >
0, то имеются источники поля и линии
вектора
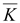 расходятся
из данной точки. Точка наблюдения
служит началом (истоком) линий вектора расходятся
из данной точки. Точка наблюдения
служит началом (истоком) линий вектора
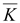 . .
Если
div
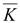 <
0, то в точке наблюдения линии вектора <
0, то в точке наблюдения линии вектора
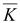 сходятся,
т.е. она служит стоком линий вектора сходятся,
т.е. она служит стоком линий вектора
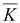 . .
Если
div
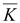 =
0, то в рассматриваемой точке
отсутствует источник линий вектора =
0, то в рассматриваемой точке
отсутствует источник линий вектора
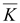 . .
Картина
электрического поля при наличии и
отсутствии зарядов показана на рис.
14.4. Например, если имеется объемный
положительный заряд +ρ, то он является
истоком вектора электрического
смещения
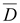 . .

Рис.
14.4. Электрическое поле при наличии
и отсутствии электрических зарядов
Дивергенция
вектора магнитной индукции
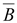 всегда
равна нулю, так как линии вектора всегда
равна нулю, так как линии вектора
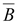 замкнуты
(не имеют начала и конца). замкнуты
(не имеют начала и конца).
В
декартовой системе координат
 (14.15) (14.15)
Ротор
(вихрь) вектора поля rot
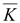 –
это вектор, характеризующий
интенсивность вихревых полей в
каждой точке. Ротор проявляет себя
как вихрь, поэтому он имеет ось.
Направление оси определяет направление
вектора, изображающего ротор. –
это вектор, характеризующий
интенсивность вихревых полей в
каждой точке. Ротор проявляет себя
как вихрь, поэтому он имеет ось.
Направление оси определяет направление
вектора, изображающего ротор.
Численно
составляющую ротора в направлении
нормали
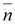 к
плоской площадке Δs
определяют как предел, к которому
стремится отношение циркуляции
вектора к площадке Δs,
ограниченной контуром интегрирования,
при стремлении ее к нулю (рис. 14.5) к
плоской площадке Δs
определяют как предел, к которому
стремится отношение циркуляции
вектора к площадке Δs,
ограниченной контуром интегрирования,
при стремлении ее к нулю (рис. 14.5)
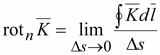 .
(14.16) .
(14.16)
Если
вихревое поле в некоторой области
не имеет внутри источников векторных
линий, то rot
 ≠
0 (div ≠
0 (div
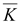 =
0). =
0).
Запишем
ротор вектора в декартовой системе
координат
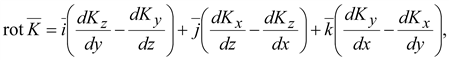 (14.17) (14.17)

Рис.
14.5. К пояснению определения ротора
вектора
где: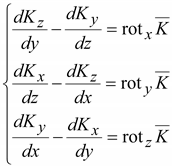 .
(14.18) .
(14.18)
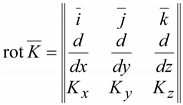 (14.19) (14.19)
|
Запись
основных векторных операций с
помощью оператора ∇
|
|
Пространственные
производные grad, div и rot можно записать
с помощью оператора ∇.
При этом умножение оператора ∇
на скалярную функцию равносильно
взятию градиента этой функции ∇φ
= grad φ. Скалярное умножение оператора
∇
и вектора дает дивергенцию этого
вектора
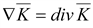 ,
а векторное их умножение образует
ротор вектора ,
а векторное их умножение образует
ротор вектора
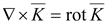 .
Применение оператора ∇
облегчает выполнение сложных
векторных операций. В табл.14.1
приведены примеры символической
записи наиболее часто встречающихся
векторных операций. .
Применение оператора ∇
облегчает выполнение сложных
векторных операций. В табл.14.1
приведены примеры символической
записи наиболее часто встречающихся
векторных операций.
Интегральные
теоремы
Теоремы
Остроградского-Гауса и Стокса
применяют при переходе от уравнений
поля, записанных в интегральной
форме, к уравнениям поля в
дифференциальной форме и наоборот.
Таблица
14.1
|
Векторная
операция
|
Символическая
запись с помощью оператора ∇
|
Примечание
|
|
1
|
2
|
3
|
|
grad
φ
|
∇φ
|
|
|
div
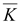
|
∇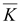
|
|
|
rot

|
∇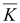
|
φ∇ + +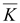 ∇φ=φdiv ∇φ=φdiv
 + +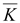 grad
φ grad
φ
|
|
div
φ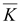
|
∇(∇φ)
|
|
|
div
grad φ
|
∇(∇φ)
= ∇2φ
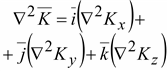
|
|
|
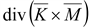
|
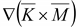
|
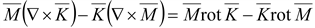
|
|
div
rot
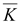
|
∇(∇ )
= 0 )
= 0
|
Исток
вихревого поля всегда отсутствует
|
|
rot
grad φ
|
∇(∇φ)
= 0
|
Векторное
поле, имеющее градиент скалярной
функции, всегда безвихревое, т.е.
потенциальное
|
|
rot
div

|
∇(∇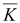 )
= 0 )
= 0
|
Векторное
поле, имеющее дивергенцию векторной
функции, всегда безвихревое
|
|
rot
rot
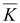
|
∇(∇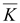 ) )
|
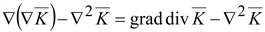
|
|
rot
φ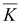
|
∇(φ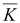 ) )
|
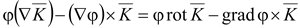
|
Теорема
Остроградского-Гауса устанавливает
соотношение между интегралом
дивергенции вектора
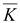 по
объему V
и поверхностным интегралом, взятым
по замкнутой поверхности s,
ограничивающей этот объем по
объему V
и поверхностным интегралом, взятым
по замкнутой поверхности s,
ограничивающей этот объем
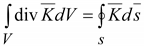 .(14.20) .(14.20)
При
этом поверхность должна быть
кусочно-гладкой, а вектор на этой
поверхности – непрерывным.
Положительной является внешняя
нормаль.
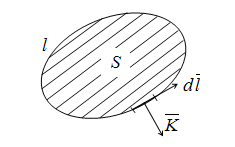
Теорема
Стокса приравнивает поверхностный
интеграл ротора вектора
 к
линейному интегралу этого вектора,
взятого по замкнутому контуру l,
ограничивающему эту поверхность к
линейному интегралу этого вектора,
взятого по замкнутому контуру l,
ограничивающему эту поверхность
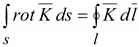 .(14.21) .(14.21)
Вектор
 должен
быть непрерывным по всему контуру
интегрирования, а контур –
кусочно-гладким. должен
быть непрерывным по всему контуру
интегрирования, а контур –
кусочно-гладким.
|
|
Понятие
об электромагнитном поле. Частные
виды электромагнитного поля
|
|
На
электромагнитное поле как на вид
материи распространяются понятия,
относящиеся к свойствам вещества:
инертная, гравитационная масса и
энергия, количество движения и
момент количества движения. Наличие
инертной массы электромагнитного
поля подтверждается опытами
великого русского ученого физика
П.Н. Лебедева, обнаружившего световое
давление на твердые тела (1899) и газы
(1907). Инертная масса электромагнитного
поля имеет ничтожную плотность.
Электромагнитное
поле является носителем гравитационной
массы, что подтверждается искривлением
светового луча в поле тяготения
Солнца, замеченным во время
солнечного затмения 1919 г., а также
тем, что энергия (скорость) луча
увеличивается при движении вниз
к земле и уменьшается при движении
вверх от земли (опыт Ландау, 1960).
Электромагнитное
поле обладает энергией, так как
при взаимодействии с заряженными
частицами их энергия изменяется
и, следовательно, передается
электромагнитному полю и наоборот.
Движение
энергии электромагнитного поля
количественно оценивается вектором
Пойнтинга. В дальнейшем будем
рассматривать макроскопическую
теорию электромагнитного поля,
которая не учитывает дискретного
распределения электрических
зарядов в веществе, считая
вещественную среду сплошной. В
этом случае для характеристики
поля используют усредненные
значения микроскопических величин
в бесконечно малом объеме, введя
четыре основные вектора
 . .
Электромагнитное
поле является совокупностью
переменных взаимосвязанных и
влияющих друг на друга электрического
и магнитного полей. Частными видами
электромагнитного поля являются:
1.
Электростатическое поле, которое
создается неподвижными заряженными
телами и проявляется в виде
механической силы, действующей на
неподвижный электрический заряд.
Это поле потенциально, т.е. rot
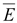 =
0. =
0.
2.
Электрическое поле постоянного
тока (стационарное электрическое
поле) образуется внутри и вне
проводников при прохождении по
ним постоянного тока. При этом
внутри однородного проводника
отсутствует объемная плотность
заряда, т.е. div
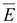 =
0. Поле является потенциальным и
для него справедливо уравнение
Лапласа ∇2φ
= 0. =
0. Поле является потенциальным и
для него справедливо уравнение
Лапласа ∇2φ
= 0.
3.
Магнитное поле постоянного потока
проявляется в силовом воздействии
на движущиеся в нем заряженные
тела и на неподвижные контуры с
постоянным током. Поле имеет
вихревой характер (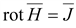 ). ).
Электрическое
поле постоянного тока и магнитное
поле постоянного потока могут
рассматриваться независимо друг
от друга.
|
|
|
Основные
характеристики электромагнитного
поля
|
|
1.
Напряженность электрического поля
– физическая характеристика
электрического поля, определяющая
силовое воздействие поля на
электрический заряд.
Напряженность
электрического поля
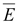 является
векторной величиной, численно равной
отношению силы является
векторной величиной, численно равной
отношению силы
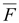 ,
с которой электрическое поле действует
на положительный заряд Q,
внесенный в рассматриваемую точку
поля, к значению этого заряда, когда
его величина стремится к нулю ,
с которой электрическое поле действует
на положительный заряд Q,
внесенный в рассматриваемую точку
поля, к значению этого заряда, когда
его величина стремится к нулю
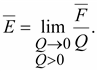 (14.22) (14.22)
За
положительное направление вектора
напряженности
 принято
направление от положительного заряда
+ Q
к отрицательному – Q
(рис. 14.6). принято
направление от положительного заряда
+ Q
к отрицательному – Q
(рис. 14.6).
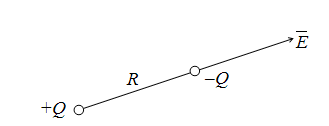
Рис.
14.6. К пояснению понятия напряженности
Сила
электрического поля, действующая
на заряд, направлена вдоль вектора
 .
Линия напряженности электрического
поля – это линия, в каждой точке
которой вектор .
Линия напряженности электрического
поля – это линия, в каждой точке
которой вектор
 касателен
к ней. Уравнение линии вектора
напряженности электрического поля: касателен
к ней. Уравнение линии вектора
напряженности электрического поля:
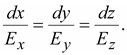 (14.23) (14.23)
где
dx,
dy, dz
– проекции элемента длины dl
вектора
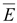 . .
Для
любой точки поля напряженность и
потенциал поля связаны выражением
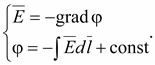 (14.24) (14.24)
Напряженность
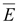 имеет
электростатическое происхождение.
Существует также напряженность имеет
электростатическое происхождение.
Существует также напряженность
 стор,
которая создается сторонними
электростатическими силами
(индукционными, термоэлектрическими,
контактными на поверхностях различных
проводников и др.). В этом случае
результирующая напряженность
электрического поля тока: стор,
которая создается сторонними
электростатическими силами
(индукционными, термоэлектрическими,
контактными на поверхностях различных
проводников и др.). В этом случае
результирующая напряженность
электрического поля тока:
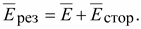 (14.25) (14.25)
2.
Магнитная индукция – это физическая
характеристика магнитного поля,
определяющая силовое воздействие
на движущийся заряд. Магнитная
индукция
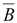 –
векторная величина, характеризующая
магнитное поле в каждой его точке. –
векторная величина, характеризующая
магнитное поле в каждой его точке.
Численно
магнитную индукцию поля можно
определить по механической силе,
действующей на один движущийся
заряд, элемент объема с заданной
плотностью тока в нем, либо на элемент
проводника с током.
Для
заряда Q,
движущегося со скоростью v
во внешнем поле:
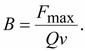 (14.26) (14.26)
Направление
силы
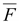 находят
по правилу векторного произведения
( находят
по правилу векторного произведения
( ).
Механическая сила ).
Механическая сила
 максимальна
при максимальна
при
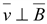 ,
и равна нулю при ,
и равна нулю при
 . .
Направление
магнитной индукции можно определить
по правилу буравчика (правого винта),
если буравчик вращать от вектора
силы
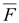 к
вектору скорости положительного
заряда Q
(рис. 14.7). к
вектору скорости положительного
заряда Q
(рис. 14.7).
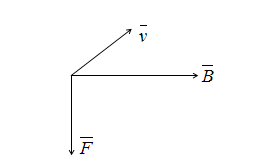
Рис.
14.7. Взаимосвязь векторов
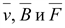
|
|
Виды
плотности тока
|
|
Английский
ученый Д.К. Максвелл ввел понятие
тока смещения в вакууме, как изменение
во времени вектора напряженности
электрического поля в вакууме,
плотность которого равна
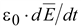 .
Ток смещения в вакууме не возникает
в результате движения электрических
зарядов, но возбуждает магнитное
поле по тем же законам, что и все виды
токов. .
Ток смещения в вакууме не возникает
в результате движения электрических
зарядов, но возбуждает магнитное
поле по тем же законам, что и все виды
токов.
Ток
смещения в диэлектрике состоит из
тока смещения в вакууме и тока
поляризации, возникающего в результате
движения связанных зарядов диэлектрика.
Плотность тока смещения в диэлектрике
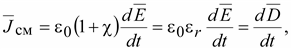 (14.27) (14.27)
где
– диэлектрическая восприимчивость,
характеризующая свойство диэлектрика
поляризоваться.
Введение
понятия тока смещения в диэлектрике
позволило Максвеллу теоретически
доказать, что энергия, излучаемая
источником электромагнитного поля,
должна распространяться по диэлектрику
в виде электромагнитных волн. В 1887
г. немецкий ученый Г. Герц экспериментально
доказал существование электромагнитных
волн.
Существуют
понятия о следующих плотностях тока.
1.
Вектор плотности тока проводимости
 (14.28) (14.28)
образуется
движением зарядов в проводящей среде
под действием постоянного или
переменного во времени поля
напряженностью
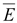 .
Он сопровождается выделением тепла
по закону Джоуля-Ленца. Линии вектора .
Он сопровождается выделением тепла
по закону Джоуля-Ленца. Линии вектора
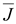 постоянного
тока непрерывны (div постоянного
тока непрерывны (div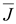 = 0). Линии вектора переменного тока
не замкнуты, поэтому
= 0). Линии вектора переменного тока
не замкнуты, поэтому
 (14.29) (14.29)
где
ρ – объемная плотность заряда.
2.
Вектор плотности тока переноса
 (14.30) (14.30)
образуется
заряженными телами и частицами,
движущимися в непроводящей среде
или в вакууме со скоростью
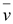 . .
3.
Вектор плотности тока поляризации
 (14.31) (14.31)
возникает
в переменном во времени поле
напряженностью
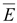 в
результате смещения связанных
зарядов молекул диэлектрика. Тепловые
потери не подчиняются закону
Джоуля-Ленца. в
результате смещения связанных
зарядов молекул диэлектрика. Тепловые
потери не подчиняются закону
Джоуля-Ленца.
4.
Вектор тока смещения в вакууме
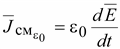 (14.32) (14.32)
существует
в вакууме только в переменном во
времени поле. Он не вызывает выделения
теплоты по закону Джоуля-Ленца.
5.
Вектор плотности тока смещения в
диэлектрике
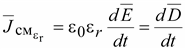 (14.32) (14.32)
наблюдается
в диэлектрике только в переменном
во времени поле. Может происходить
выделение теплоты, но не по закону
Джоуля-Ленца. На поверхности проводника
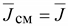 . .
6.
Вектор плотности полного тока
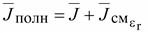 при при
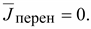 (14.34) (14.34)
Линии
плотности полного тока всегда
замкнуты
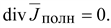 (14.35) (14.35)
Общим
свойством для всех видов тока является
создание магнитного поля, описываемого
уравнением Максвелла
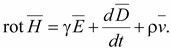 (14.36) (14.36)
|
|
Формы
записи уравнений Максвелла
|
|
Уравнения
Максвелла являются фундаментальными
уравнениями электромагнитного поля.
Эти уравнения могут быть записаны
в интегральной, дифференциальной
или комплексной форме. Интегральная
форма записи уравнений устанавливает
связь между величинами в разных
точках поля или на разных отрезках,
поверхностях. Дифференциальная
форма описывает соотношение между
величинами вблизи одной и той же
точки поля в определенный момент
времени. Эту форму записи применяют
при исследовании полей, изменяющихся
от точки к точке. Гармонически
изменяющиеся электромагнитные поля
(когда проекции вектора на координатные
оси являются гармоническими функциями
времени) удобно характеризовать
уравнениями Максвелла в комплексной
форме.
Переход
от интегральной формы записи уравнений
к дифференциальной осуществляется
с помощью теорем Остроградского-Гаусса
и Стокса (14.20) и (14.21).
Система
уравнений электромагнитного поля
включает в себя четыре основных
уравнения Максвелла и уравнения
связи между векторами поля и
параметрами
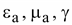 ,
характеризующими свойства среды. ,
характеризующими свойства среды.
1.
Закон полного тока – первое уравнение
Максвелла
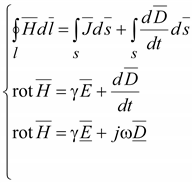 .
(14.37) .
(14.37)
Ток
смещения
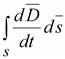 ,
также как и ток проводимости ,
также как и ток проводимости
 ,
создает магнитное поле. Изменяющееся
во времени электрическое поле создает
магнитное поле. Направление вектора
напряженности магнитного поля ,
создает магнитное поле. Изменяющееся
во времени электрическое поле создает
магнитное поле. Направление вектора
напряженности магнитного поля
 связано
с направлением полного тока и
определяется правилом правоходового
винта. связано
с направлением полного тока и
определяется правилом правоходового
винта.
2.
Закон электромагнитной индукции –
второе уравнение Максвелла
 (14.38) (14.38)
Изменение
магнитной индукции во времени создает
электрическое поле, направление
которого связано с направлением
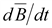 и
определяется правилом левоходового
винта. и
определяется правилом левоходового
винта.
3.
Принцип непрерывности магнитных
силовых линий
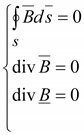 .
(14.39) .
(14.39)
Магнитный
поток через замкнутую поверхность
равен нулю. Магнитные силовые линии
всегда замкнуты и не имеют ни истоков,
ни стоков.
4.
Обобщенная теорема Гаусса
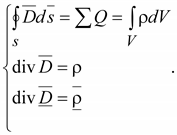 (14.40) (14.40)
Поток
вектора электрического смещения
через замкнутую поверхность равен
алгебраической сумме свободных
зарядов, находящихся внутри замкнутой
поверхности.
5.
Уравнения связи между векторами
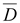 и и
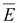 , ,
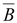 и и
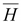 , ,
 и и
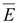 в
материальной среде в
материальной среде
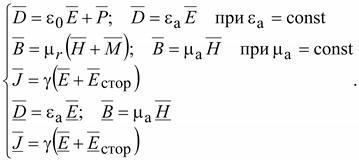 .
(14.41) .
(14.41)
|
|
Напряженность
и потенциал электростатического
поля
|
|
Электростатическое
поле создается совокупностью
электрических зарядов, неподвижных
в пространстве по отношению к
наблюдателю и неизменных во времени.
В
теории поля усредняют микроскопические
неоднородности вещества (на
элементарном уровне) в пространстве
и во времени, т.е. рассматривают
процессы в макроскопическом смысле.
Под зарядом тела понимают скалярную
величину, равную алгебраической
сумме элементарных электрических
зарядов в этом теле.
В
дальнейшем будем иметь дело с полем,
создаваемым в однородных и изотропных
средах, т.е. в таких средах, электрические
свойства которых одинаковы для всех
точек поля и не зависят от направления.
Электростатическое поле обладает
способностью воздействовать на
помещенный в него электрический
заряд с механической силой, прямо
пропорциональной величине этого
заряда. В основу определения
электрического поля положено
механическое его проявление. Оно
описывается законом Кулона, который
характеризует силу взаимодействия
двух точечных зарядов.
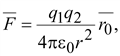 (15.1) (15.1)
где
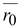 –
единичный вектор, направленный по
линии, соединяющей заряды. –
единичный вектор, направленный по
линии, соединяющей заряды.
Если
размеры тел, на которых расположены
взаимодействующие заряды, много
меньше расстояния между ними, то
говорят о точечных зарядах.
Основными
величинами, характеризующими
электростатическое поле, являются
напряженность
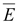 и
потенциал φ. и
потенциал φ.
Потенциал
φ является скалярной величиной, и
его значение в каждой точке поля
определяется некоторым числом.
Электростатическое
поле определено, если известен закон
изменения напряженности и потенциала
во всех точках этого поля.
Понятие
потенциала связано с работой,
совершаемой силами поля при перемещении
заряда:
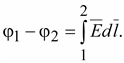 (15.2) (15.2)
Разность
потенциалов между исходной и конечной
точками пути (точками 1 и 2) зависит
только от положения этих точек и не
зависит от пути, по которому
определялась разность потенциалов.
Если пройти по замкнутому пути, то
исходная и конечная точки совпадут,
т.е.
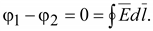 (15.3) (15.3)
Циркуляция
вектора
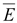 вдоль
любого замкнутого контура равна
нулю. вдоль
любого замкнутого контура равна
нулю.
Это
основное свойство электростатического
поля. Такое поле носит название
потенциального. Потенциальными
также являются гравитационное поле,
установившиеся температурные поля
и др.
Электростатическое
поле можно охарактеризовать
совокупностью силовых и эквипотенциальных
линий.
Силовая
линия – это мысленно проведенная в
поле линия, начинающаяся на положительно
заряженном теле и оканчивающаяся
на отрицательно заряженном теле,
касательная к которой в каждой точке
дает направление напряженности
поля.
Эквипотенциальные
(равнопотенциальные) поверхности
представляют собой совокупность
точек поля, имеющих одинаковый
потенциал. Линии равного потенциала
называются эквипотенциальными.
Эквипотенциальные
и силовые линии в любой точке поля
пересекаются под прямым углом (рис.
15.1).
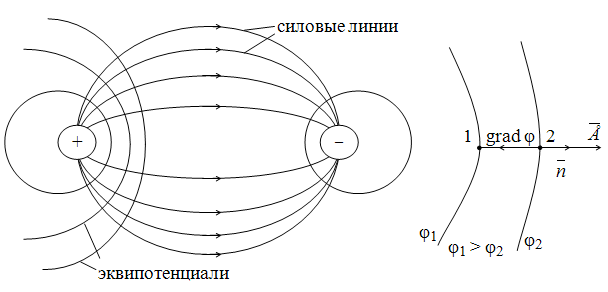
Рис.
15.1. Картина электрического поля
Между
точками 1 и 2 всегда имеется разность
потенциалов. Разделив эту разность
на кратчайшее расстояние между этими
точками, получим скорость изменения
потенциала в этом направлении. При
стремлении расстояния между точками
к нулю
 (15.4) (15.4)
Так
как направление векторов
 и и
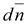 совпадают,
то можно записать: совпадают,
то можно записать:
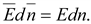
Модуль
вектора напряженности поля E
= –dφ/dn.
Вектор
напряженности можно записать, как
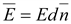 .
Тогда .
Тогда
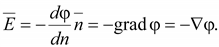 (15.5) (15.5)
Напряженность
в какой-либо точке поля равна скорости
изменения потенциала в этой точке,
взятой с обратным знаком.
В
общем случае
 (15.6) (15.6)
Тогда
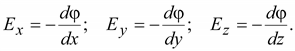 (15.7) (15.7)
|
Поляризация
вещества. Вектор электрического
смещения
|
|
Свободными
называются заряды, которые под
воздействием сил поля могут свободно
перемещаться в веществе, их
перемещение не ограничено
внутримолекулярными силами.
Связанными называют заряды, входящие
в состав вещества и удерживаемые
в определенных положениях
внутримолекулярными силами. Эти
заряды связаны с самим веществом
и неотделимы от него.
При
наличии внешнего электростатического
поля напряженностью
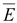 молекулы
диэлектрика деформируются.
Положительный заряд смещается по
направлению внешнего поля, а
отрицательный – в противоположном
направлении, образуя диполь –
связанный заряд. В диэлектриках,
имеющих дипольные молекулы, их
электрические моменты под влиянием
внешнего поля частично ориентируются
по направлению поля. У большинства
диэлектриков направление вектора
поляризованности молекулы
диэлектрика деформируются.
Положительный заряд смещается по
направлению внешнего поля, а
отрицательный – в противоположном
направлении, образуя диполь –
связанный заряд. В диэлектриках,
имеющих дипольные молекулы, их
электрические моменты под влиянием
внешнего поля частично ориентируются
по направлению поля. У большинства
диэлектриков направление вектора
поляризованности
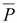 совпадает
с направлением вектора напряженности
внешнего поля, а направление вектора
напряженности поляризованных
зарядов совпадает
с направлением вектора напряженности
внешнего поля, а направление вектора
напряженности поляризованных
зарядов
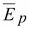 противоположно
направлению вектора напряженности
внешнего поля (от + Q
к – Q).
Поэтому результирующий вектор
напряженности поля в диэлектрике противоположно
направлению вектора напряженности
внешнего поля (от + Q
к – Q).
Поэтому результирующий вектор
напряженности поля в диэлектрике
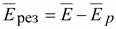 меньше
вектора напряженности поля в
вакууме при одном и том же внешнем
поле (рис. 15.2). меньше
вектора напряженности поля в
вакууме при одном и том же внешнем
поле (рис. 15.2).
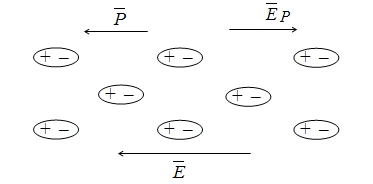
Рис.
15.2. Поляризация диполей во внешнем
поле
С
увеличением поляризации диэлектрика
увеличивается вектор
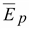 .
Вектор поляризованности определяют
по геометрической сумме электрических
моментов диполей в единице объема .
Вектор поляризованности определяют
по геометрической сумме электрических
моментов диполей в единице объема
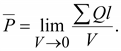 (15.8) (15.8)
Для
большинства диэлектриков
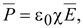 (15.9) (15.9)
где
– относительная диэлектрическая
восприимчивость.
В
электротехнических расчетах
используется также вектор
электрического смещения (индукции):
 ,(15.10) ,(15.10)
где
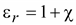 . .
Вектор
 зависит
как от свободных, так и от связанных
зарядов. зависит
как от свободных, так и от связанных
зарядов.
|
|
Теорема
Гаусса в интегральной форме
|
|
Формулируется
тремя способами:
1.
Поток вектора электрического
смещения через любую замкнутую
поверхность, окружающую некоторый
объем, равен алгебраической сумме
свободных зарядов, находящихся
внутри этой поверхности
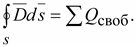 (15.11) (15.11)
Вектор
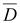 –
это такая характеристика поля,
которая не зависит от диэлектрических
свойств среды. –
это такая характеристика поля,
которая не зависит от диэлектрических
свойств среды.
2.
Так как
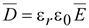 ,
то теорему Гаусса для однородной
и изотропной среды можно записать: ,
то теорему Гаусса для однородной
и изотропной среды можно записать:
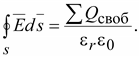 (15.12) (15.12)
Вектор
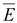 –
это характеристика поля, которая
зависит от диэлектрических свойств
среды. –
это характеристика поля, которая
зависит от диэлектрических свойств
среды.
3.
Поток вектора
 через
любую замкнутую поверхность
создается не только суммой свободных
зарядов, но и суммой связанных
зарядов через
любую замкнутую поверхность
создается не только суммой свободных
зарядов, но и суммой связанных
зарядов
 .
(15.13) .
(15.13)
Теорему
Гаусса можно использовать для
нахождения напряженности или
электрического смещения в какой-либо
точке поля, если через эту точку
можно провести замкнутую поверхность
таким образом, что все ее точки
будут в симметричных (одинаковых
условиях по отношению к заряду,
находящемуся внутри замкнутой
поверхности).
Такой
поверхностью являются обычно сфера
(если заряд точечный), или боковая
поверхность цилиндра (если заряд
линейный).
В
качестве примера использования
теоремы Гаусса найдем напряженность
поля, создаваемую точечным зарядом
в точке, удаленной на расстояние
r
от за��яда. С этой целью через
заданную точку проведем сферическую
поверхность радиусом r,
полагая, что заряд находится в
центре сферы (рис. 15.3).
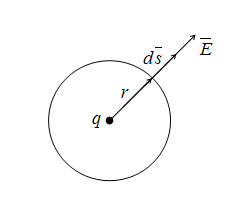
Рис.
15.3. К определению поля точечного
заряда
Элемент
поверхности сферы
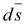 перпендикулярен
поверхности сферы и направлен в
сторону внешней нормали, т.е. векторы перпендикулярен
поверхности сферы и направлен в
сторону внешней нормали, т.е. векторы
 и и
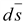 в
каждой точке сферы совпадают по
направлению в
каждой точке сферы совпадают по
направлению
 (15.14) (15.14)
Напряженность
поля:
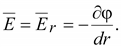
Откуда
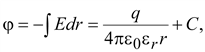 (15.15) (15.15)
где
C
– постоянная интегрирования.
|
|
Теорема
Гаусса в дифференциальной форме
|
|
С
помощью интегральной теоремы
Гаусса нельзя определить, как
связан исток линий
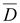 в
данной точке поля с плотностью
свободных зарядов в той же точке
поля. Поэтому переходят к записи
теоремы Гаусса в дифференциальной
форме: в
данной точке поля с плотностью
свободных зарядов в той же точке
поля. Поэтому переходят к записи
теоремы Гаусса в дифференциальной
форме:
 (15.16) (15.16)
Исток
линий
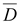 в
данной точке поля определяется
величиной плотности свободных
зарядов в этой точке (рис. 15.4). в
данной точке поля определяется
величиной плотности свободных
зарядов в этой точке (рис. 15.4).
Если
среда однородна и изотропна, т.е.
εa
=
const,
то можно записать:
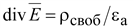 (15.17) (15.17)
или:
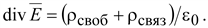 (15.18) (15.18)
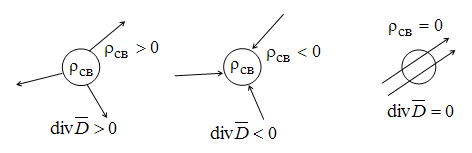
Рис.
15.4. К пояснению истока линий вектора
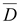
Истоком
вектора
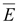 в
отличие от истока вектора в
отличие от истока вектора
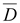 являются
не только свободные, но и связанные
заряды. являются
не только свободные, но и связанные
заряды.
С
другой стороны известно, что

С
учетом этого
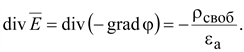
Или
 (15.19) (15.19)
Уравнение
(15.19) называется уравнением Пуассона.
Частный вид уравнения Пуассона
при ρсв
= 0, называется уравнением Лапласа
 . .
Эти
два уравнения являются основными
уравнениями электростатики.
Уравнение Пуассона выражает связь
между частными производными второго
порядка от φ в любой точке поля и
плотностью свободных зарядов в
этой точке поля.
Решение
уравнения Пуассона в общем виде
можно найти следующим образом.
Положим, что в объеме V
есть объемные ρ, поверхностные σ
и линейные τ заряды. Эти заряды
представим в виде совокупности
точечных зарядов: ρdV,
σds
и τdl,
где dV
– элемент объема, ds
– элемент заряженной поверхности,
dl
– элемент длинны заряженной оси.
Составляющая потенциала dφ
в некоторой точке пространства,
удаленной от ρdV
на расстояние r,
в соответствии с формулой (15.15)
равна
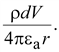
Аналогично
можно определить составляющие
потенциала от поверхностного и
линейного зарядов
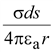 и и
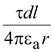 . .
Полное
значение φ определяется как сумма
(интеграл) составляющих потенциала
от всех зарядов поля:
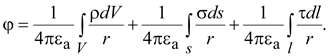 (15.20) (15.20)
В
формуле (15.20) ρ, σ и τ есть функции
радиуса r,
которые практически определить
очень трудно. Предполагается, что
потенциал на бесконечности равен
нулю и заряды, создающие поля
распределены в ограниченной области
(иначе интеграл может оказаться
расходящимся).
|
|
Граничные
условия
|
|
Под
граничными условиями понимают
условия, которым подчиняется поле
на границах раздела сред с различными
электрическими свойствами.
При
интегрировании уравнения Лапласа
(или Пуассона) в решение входят
постоянные интегрирования. Их
определяют из граничных условий.
В
проводящем теле, находящемся в
магнитном поле, вследствие явления
электростатической индукции
происходит разделение зарядов
(рис. 15.5).
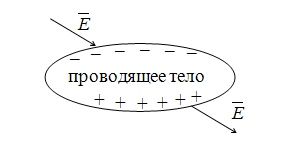
Рис.
15.5. разделение зарядов в проводящем
теле
Все
точки тела будут иметь один и тот
же потенциал (иначе появилось бы
упорядоченное движение зарядов).
Поверхность тела эквипотенциальна.
Вектор напряженности внешнего
поля в любой точке поверхности
подходит к ней под прямым углом.
Внутри проводящего тела напряженность
равна нулю, так как внешнее поле
компенсируется полем зарядов,
расположившихся на поверхности
тела.
На
границе раздела проводящего тела
и диэлектрика при отсутствии тока
по проводящему телу выполняются
два условия:
1.
Отсутствует тангенциальная
(касательная к поверхности)
составляющая напряженности поля
 (15.21) (15.21)
2.
Вектор электрического смещения
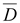 в
любой точке диэлектрика,
непосредственно примыкающей к
поверхности проводящего тела,
численно равен плотности заряда
σ на поверхности проводящего тела
в этой точке: в
любой точке диэлектрика,
непосредственно примыкающей к
поверхности проводящего тела,
численно равен плотности заряда
σ на поверхности проводящего тела
в этой точке:
 (15.22) (15.22)
На
границе раздела двух диэлектриков
с различными диэлектрическими
проницаемостями выполняются
следующие условия:
1.
Тангенциальные составляющие
напряженности поля равны:
Et1
= Et2.
(15.23)
2.
Нормальные составляющие электрической
индукции равны:
Dn1
= Dn2.
(15.24)
Уравнения
Лапласа и Пуассона являются
уравнениями в частных производных,
которые в общем случае имеют
множество линейно независимых
друг от друга решений. Выбор
единственного решения, удовлетворяющего
конкретной задаче, производят с
помощью граничных условий.
|
|
Общая
характеристика задач электростатики
и методов их решения
|
|
В
зависимости от того, что задано и
что необходимо определить, задачи
электростатики можно подразделить
на три типа.
1.
По заданному закону распределения
потенциала в пространстве φ(x,
y,
z)
найти распределение свободных
зарядов, вызвавших поле.
Такого
рода задачи можно решать с помощью
уравнений Пуассона. Это наиболее
простой тип задач.
2.
Задан закон распределения свободных
зарядов в пространстве в функции
координат ρсвоб(x,
y,
z).
Требуется найти закон изменения
потенциала в пространстве φ(x,
y,
z).
Эта
задача является обратной по
отношению к первой и значительно
сложнее ее.
Принципиально
задача состоит в решении уравнения
Пуассона относительно φ, т.е. в
решении дифференциального уравнения
второго порядка в частных производных.
Задачи
первого и второго типа на практике
встречаются редко, чаще приходится
иметь дело с задачами третьего
типа.
3.
Известны потенциалы (или полные
заряды) и геометрия тел, создающих
поле. Требуется найти закон изменения
напряженности или потенциала во
всех точках поля.
Если
среда, в которой создано поле,
является неоднородной, то ее
подразделяют на однородные области,
и решение уравнения Лапласа
производят для каждой области
отдельно. Основная трудность задачи
состоит в том, что хотя полные
заряды тел и известны, но плотность
распределения зарядов на отдельных
участках заряженного тела неизвестна.
Решения уравнений Лапласа для
отдельных областей должны быть
согласованы друг с другом: на
границе раздела двух сред с
различными диэлектрическими
проницаемостями должны выполняться
граничные условия.
Задачи
третьего типа можно решать
аналитически, графически либо
путем моделирования.
|
|
Под
заряженной осью понимают тонкий,
теоретически бесконечно длинный
металлический проводник.
Под
линейной плотностью заряда τ
понимают заряд, приходящийся на
единицу длины оси.
Пусть
диэлектрическая проницаемость
окружающей среды равна εa.
Для
нахождения напряженности поля в
некоторой точке, удаленной на
расстояние r
от оси, проведем через точку
цилиндрическую поверхность так,
чтобы ее ось совпала с заряженной
осью (рис. 15.6).

Рис.
15.6. К определению поля заряженной
оси
Используем
теорему Гаусса, которая применима
к замкнутой поверхности (боковая
поверхность цилиндра и два его
основания). Поток вектора
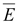 имеется
только через боковую поверхность.
Направление имеется
только через боковую поверхность.
Направление
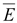 и и
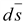 на
боковой поверхности в каждой точке
совпадают, поэтому на
боковой поверхности в каждой точке
совпадают, поэтому

или
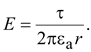 (15.25) (15.25)
Напряженность
в поле заряженной оси изменяется
обратно пропорционально расстоянию
r
точки от оси.
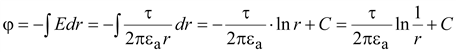 (15.26) (15.26)
Потенциал
изменяется по экспоненциальному
закону.
Электрическая
емкость определяется как отношение
заряда к разности потенциалов
между телами. Рассчитаем емкость
двух соосных цилиндров (рис. 15.7).

Рис.
15.7. Разрез двух соосных цилиндров
Напряжение
между поверхностями цилиндров
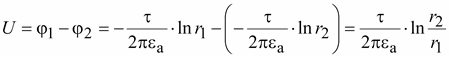 . .
Емкость
цилиндрического конденсатора
будет равна
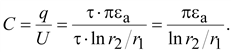 (15.27) (15.27)
|
|
Поле
двух параллельных заряженных осей
|
|
Пусть
одна ось имеет линейный заряд + τ,
а другая – - τ. Возьмем в поле
некоторую произвольную точку М
(рис. 15.8).
Результирующая
напряженность поля в точке М
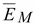 равна
геометрической сумме напряженностей
от обоих зарядов. Потенциал –
функция скалярная, и он равен сумме
потенциалов от каждой оси равна
геометрической сумме напряженностей
от обоих зарядов. Потенциал –
функция скалярная, и он равен сумме
потенциалов от каждой оси
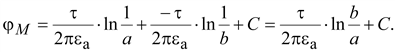 (15.28) (15.28)
Уравнением
эквипотенциали в поле двух заряженных
осей является выражение b/a
= const, т.е. эквипотенциаль представляет
собой совокупность точек, отношение
расстояний которых до двух заданных
точек есть величина постоянная.
Из геометрии известно, что такой
совокупностью точек является
окружность. Для ее построения
соединим точку М
с осями. Проведем биссектрису
внутреннего (aMb)
и внешнего (pMa)
углов. Точки 1 и 2 пересечения
биссектрис с линией, проведенной
через заряженные оси, и точка М
будут тремя точками окружности.
Для нахождения положения центра
окружности (точки О)
разделим пополам расстояние между
точками 1 и 2.
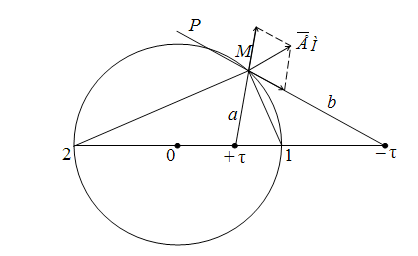
Рис.
15.8. Поле двух заряженных осей
Рассмотрим
поле двухпроводной линии (рис.
15.9).
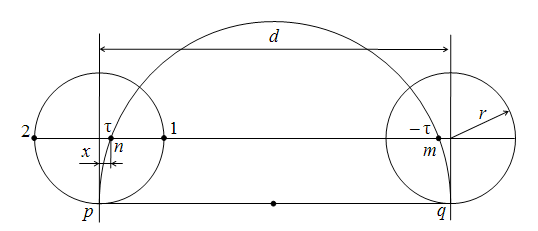
Рис.
15.9. К рассмотрению поля двухпроводной
линии
Заряды
проводов по поверхности распределены
с неодинаковой плотностью.
Задача
о поле двухпроводной линии может
быть сведена к задаче о поле двух
заряженных осей.
Пусть
заряженные оси будут расположены
в точках m
и n.
Из условия симметрии они удалены
на одинаковое расстояние x
от геометрических осей проводов
О2
и О1.
Для
точки 1 отношение b/a
будет
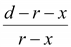 ,
для точки 2 – ,
для точки 2 –
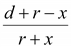 . .
Из
равенства
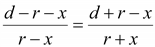 получим получим
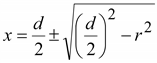 .
(15.29) .
(15.29)
Знак
минус перед радикалом соответствует
положению точки n,
знак плюс – точке m.
Точки
m
и n
называют электрическими осями
проводов. Их можно получить
геометрическим построением.
Проводится линия, параллельная
линии, соединяющей оси проводов и
касательная к поверхности проводов.
Через точки касания поводится
окружность диаметром d.
Пересечение этой окружности с
линией соединяющей оси проводов
даст положение электрических осей.
Определим емкость
двухпроводной линии
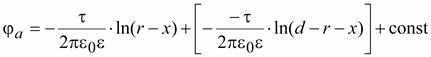 ; ;
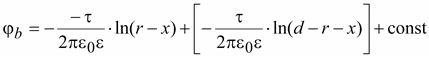 ; ;
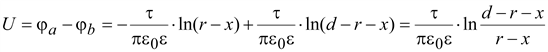 ; ;
 .
(15.30) .
(15.30)
|
|
Поле
заряженной оси, расположенной
вблизи проводящей плоскости
|
|
Ось
расположена параллельно плоскости
на расстоянии h
от нее (рис. 15.10). Требуется определить
характер поля в диэлектрике.
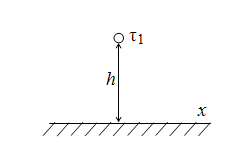
Рис.
15.10. Ось вблизи проводящей поверхности
В
результате электростатической
индукции на поверхности проводящего
тела выступают заряды. Плотность
их меняется с изменением координаты
x.
Поле в диэлектрике создается всеми
зарядами.
Для
расчета поля в проводящую среду
помещают фиктивный заряд на
расстоянии h.
При этом среда по обе стороны
границы считается однородной (рис.
15.11).
Проводящая
поверхность эквипотенциальна (φ
= const). Тогда потенциал ее равен
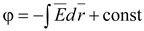 . .
При
этом изменение потенциала вдоль
поверхности
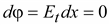 . .
Следовательно,
граничным условием будет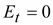 . .

Рис.
15.11. Расчетная схема
Тогда
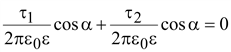 . .
Отсюда
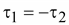 . .
Потенциал
в любой точке верхней полусферы
будет равен
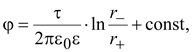 (15.31) (15.31)
где
r–
– расстояние до отрицательно
заряженной оси,
r+
– расстояние до положительно
заряженной оси.
Потенциал
провода
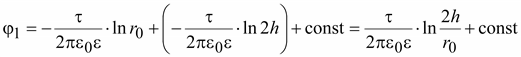 ,
(15.32) ,
(15.32)
где
r0
– радиус провода.
Разность
потенциалов
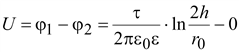 (15.33) (15.33)
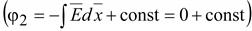 . .
Емкость
провода
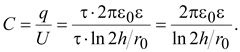 (15.34) (15.34)
Емкость
провода относительно земли в два
раза выше емкости двухпроводной
линии.
Распределение
заряда на границе раздела диэлектрика
и проводника
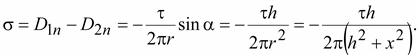 (15.35) (15.35)
|
Поле
заряженной оси, расположенной
вблизи границы раздела двух
диэлектриков
|
|
Рассмотрим
поле оси, расположенной на
расстоянии h
от границы раздела двух диэлектриков
с диэлектрическими проницаемостями
ε1
и ε2
(рис. 15.12).
Вследствие
поляризации диэлектриков на
границе раздела выявятся связанные
заряды, влияющие на поле в обеих
средах. Учет их влияния на поле
проводят путем введения двух
дополнительных зарядов τ2
и τ3
(рис. 15.13).
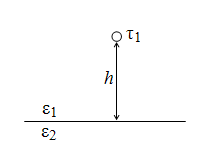
Рис.
15.12. Ось, расположенная вблизи
раздела диэлектриков
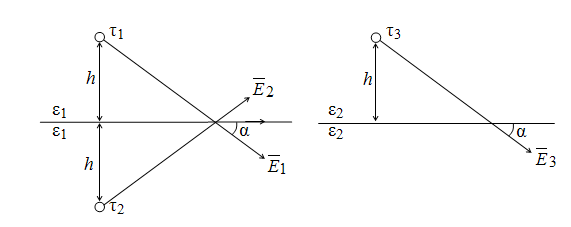
Рис.
15.13. Расчетная схема поля
Расчет
поля в верхней полусфере ведется
от двух зарядов: реального τ1
и фиктивного τ2,
расположенных симметрично
относительно границы раздела,
причем среда всюду имеет
диэлектрическую проницаемость
ε1.
Расчет
поля в нижней полусфере ведется
от заряда τ3,
расположенного в той же точке,
что и τ1.
Среда при этом всюду имеет
проницаемость ε2.
Граничные
условия реальной задачи
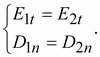
В
данном случае
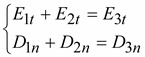 , ,
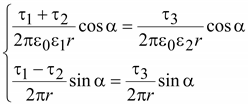 . .
Откуда
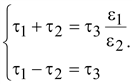
Решая
эту систему, получим
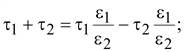
 .
(15.36) .
(15.36)
Знак
заряда τ2
совпадает со знаком заряда τ1,
если ε1
> ε2.
Знак заряда τ3
всегда тот же, что и знак τ1.
|
|
|
|
|
Поле
двухпроводной линии над
поверхностью земли
|
|
Для
расчета поля введем две
дополнительные оси. Определим
потенциал произвольной точки M
(рис. 15.14).
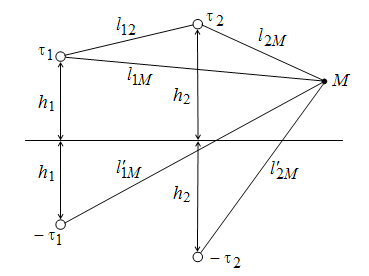
Рис.
15.14. К расчету поля двухпроводной
линии в произвольной точке
Согласно
(15.30) потенциал произвольной точки
от заряженной оси
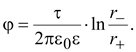
В
данном случае
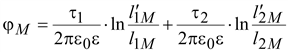
или
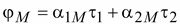 ,
(15.37) ,
(15.37)
где
1M
и 2M
– потенциальные коэффициенты,
зависящие от характера среды и
расположения проводов.
Уравнение
(15.36) показывает, что потенциал
прямо пропорционален заряду.
Потенциалы
проводов можно записать в виде
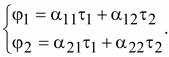 (15.38) (15.38)
Эти
уравнения называются первой
группой формул Максвелла.
С
учетом расстояний, показанных
на рис. 15.15, потенциальные
коэффициенты можно определить
по формулам:

Рис.
15.15. Размеры картины поля с учетом
размера проводов
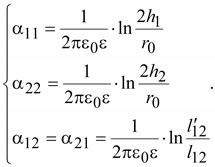 (15.39) (15.39)
Коэффициент
11
численно равен потенциалу φ1,
когда на первом проводе находится
единичный заряд, а на других
проводах заряд отсутствует.
Коэффициент
12
численно равен потенциалу φ1,
когда на втором проводе находится
единичный заряд, а на других
проводах заряд отсутствует.
Аналогично
можно описать другие потенциальные
коэффициенты.
Решив
систему (15.37) относительно зарядов,
получим вторую группу формул
Максвелла.
 (15.40) (15.40)
Коэффициенты
называют емкостными коэффициентами.
Их размерность обратна размерности
потенциальных коэффициентов.
Коэффициенты с одинаковыми
индексами положительны, а с
разными – отрицательны.
Если
ввести частичные емкости между
проводами линии и землей (рис.
15.16), то заряды можно записать в
виде

или
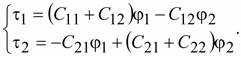 (15.41) (15.41)
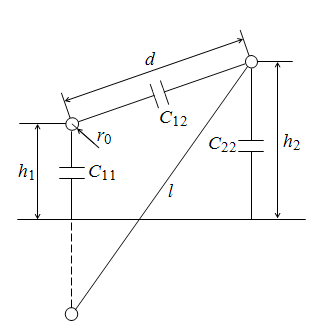
Рис.
15.16. Частичные емкости линии
Емкости
C11,
C22
называются собственными частичными
емкостями, C12
и C21
– взаимными частичные емкости.
Из
сравнения систем (15.39) и (15.40) видно,
что
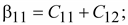 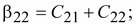 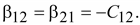
Откуда
следует, что
 , ,
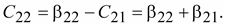
Если
к проводам подведено напряжение
U
от незаземленного источника, то
провода заряжаются так, что
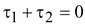 ,
или ,
или
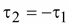 . .
В
этом случае можно говорить о
рабочей емкости линии
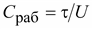 . .
Подставив
значение
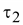 в
уравнение (15.41) получим в
уравнение (15.41) получим

При
этом рабочая емкость будет равна
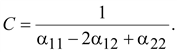 (15.42) (15.42)
Согласно
(15.38)
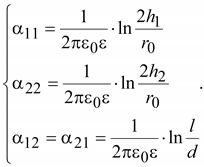
Подставив
эти значения в (15.42) получим
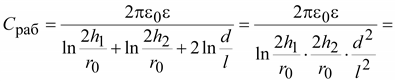
 (15.43) (15.43)
Величина
 определяет
влияние земли на величину емкости. определяет
влияние земли на величину емкости.
(Так
как
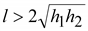 ,
то близость земли увеличивает
емкость системы двух проводов.) ,
то близость земли увеличивает
емкость системы двух проводов.)
|
|
|
|
|
Расчет
поля плоского конденсатора
|
|
Рассмотри
плоский конденсатор (рис. 15.17а).
Расстояние между пластинами
конденсатора – d.
К обкладкам приложено напряжение
– U.
Свободные заряды между пластинами
отсутствуют. Требуется рассчитать
поле между пластинами.
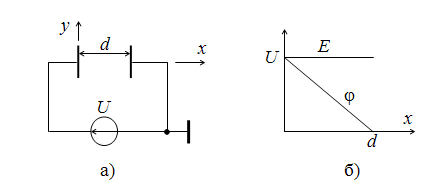
Рис.
15.17. Поле плоского конденсатора
при отсутствии зарядов
Поле
при отсутствии в расчетной области
свободных зарядов подчиняется
уравнению Лапласа:
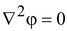 . .
В
общем случае это уравнение
записывается
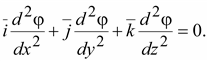
Если
предположить, что в направлении
осей y
и z
поле не меняется, то уравнение
упрощается:

После
интегрирования получаем
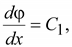
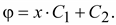
Постоянные
интегрирования находятся из
граничных условий.
Без
нарушения картины распределения
поля можно принять потенциал
одной из пластин, равным нулю.
Тогда потенциал другой будет
равен приложенному напряжению.
При x
= 0 потенциал φ = U;
а при x
= d
– φ = 0:
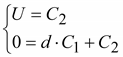 ; ;
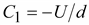 ; ;
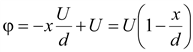 .(15.44) .(15.44)
Следовательно,
между пластинами потенциал
линейно уменьшается от величины
U
до нуля (рис. 15.17б).
Напряженность
поля
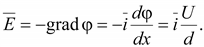 (15.45) (15.45)
Напряженность
поля не зависит от координаты x
и численно равна U/d.
|
|
Расчет
поля плоского конденсатора при
наличии свободных зарядов
|
|
Рассмотрим
поле конденсатора, когда между
пластинами имеются свободные
заряды плотностью ρ (рис. 15.18).
Поле
между пластинами подчиняется
уравнению Пуассона

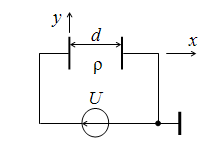
Рис.
15.18. К расчету поля конденсатора
при наличии свободных зарядов
между пластинами
Допустим,
что поле по осям y
и z
не изменяется. Тогда
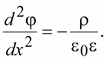 (15.46) (15.46)
После
интегрирования получим
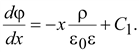
Общее
решение уравнения (15.46)
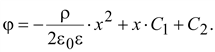 (15.47) (15.47)
Граничные
условия в этом случае те же, что
и в предыдущей задаче.
При
x
= 0 потенциал φ = U,
а при x
= d
– φ = 0:
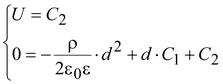 ; ;
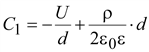
Потенциал
изменяется по закону
 (15.48) (15.48)
Напряженность
поля
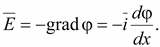
Модуль
напряженности
 (15.49) (15.49)
Напряженность
поля при наличии свободных зарядов
не постоянна. Она прямо
пропорциональна расстоянию от
начала отсчета по оси x.
|
|
|
|
|
Влияние
диэлектрического цилиндра на
форму поля
|
|
Цилиндр
радиусаr0
с проницаемостью ε1
помещен
во внешнее плоскопараллельное
поле напряженностью E0
(рис. 15.19). Вектор напряженности
направлен по нормали к оси
цилиндра. Внешняя среда имеет
проницаемость ε2.

Рис.
15.19. Диэлектрический цилиндр в
электрическом поле
Требуется
рассчитать поле как внутри, так
и вне цилиндра.
Для
решения задачи будем использовать
уравнение Лапласа, записанное в
цилиндрической системе координат
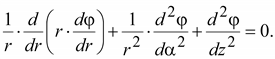 (15.50) (15.50)
Будем
считать, что внешнее поле по оси
z
не изменяется. При этом
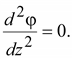
Так
как рассматриваемая среда имеет
две области с различной
диэлектрической проницаемостью,
то дифференциальное уравнение
(15.50) решается отдельно для обеих
сред.
Для
поля внутри цилиндра
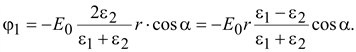 (15.51) (15.51)
Для
поля вне цилиндра
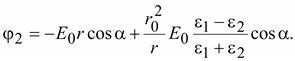 (15.52) (15.52)
Найдем
закон распределения напряженности
поля.
Внутри
цилиндра (r
< r0)
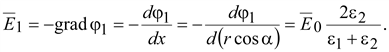 (15.53) (15.53)
Следовательно,
поле ориентировано по направлению
внешнего поля.
При
ε1
> ε2
E1
< E0,
при ε1
< ε2
E1
> E0.
Таким
образом, можно записать
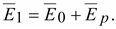
Учитывая,
что вектора
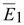 и и
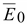 ориентированы
одинаково ориентированы
одинаково
 (15.54) (15.54)
По
модулю вектор напряженности
поля, обусловленный поляризацией,
меньше вектора напряженности
внешнего поля. А направление его
зависит от соотношения
диэлектрических проницаемостей
 и и
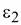 . .
За
пределами цилиндра (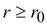 ) )
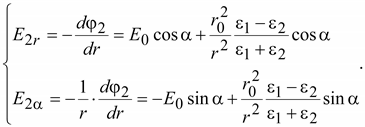 (15.55) (15.55)
В
случае внесения в поле металлического
цилиндра (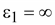 ) )
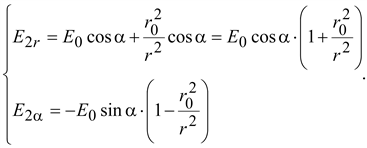 (15.56) (15.56)
|
|
Вектор
электрического смещения в общем
виде записывается
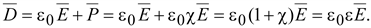 (15.57) (15.57)
В
этом уравнении считается, что
поляризация вещества происходит
мгновенно, или же происходит
медленное изменение магнитного
поля, т.е. рассматривается
квазистатическое поле.
Рассмотрим,
как происходит поляризация в
реальных условиях.
В
гидродинамике вязкость записывается
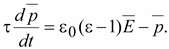
Первое
слагаемое показывает статическое
значение поляризации, а второе
– поляризацию в данный момент
времени.
С
учетом 1 +
= ε уравнение (15.56) можно переписать
в виде
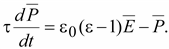
Допустим,
что поле изменяется синусоидальному
закону. В этом случае целесообразно
прейти к комплексной форме записи.

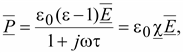 (15.58) (15.58)
где
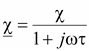 –
комплексная диэлектрическая
восприимчивость, тогда –
комплексная диэлектрическая
восприимчивость, тогда
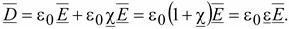 (15.59) (15.59)
Это
уравнение полностью аналогично
уравнению (15.10).
Комплексная
диэлектрическая проницаемость
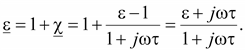 (15.60) (15.60)
Если
избавиться от иррациональности
в знаменателе, то
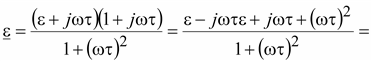
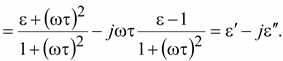
Таким
образом, введение понятия вязкости
привело к зависимости диэлектрической
проницаемости от частоты.
При
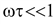
 (15.61) (15.61)
т.е.
на низких частотах вязкие свойства
отсутствуют, и поляризация
происходит мгновенно.
При
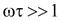
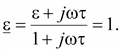 (15.62) (15.62)
Следовательно,
на высоких частотах ε = 1, т.е. среда
обладает свойствами вакуума, и
поляризация не происходит, так
как молекулы не успевают
подстраиваться к полю.
|
|
Если
под воздействием внешних источников
в проводящей среде создано
электрическое поле, то в ней будет
протекать электрический ток.
Свойство среды, характеризующее
ее способность проводить ток,
называется удельной проводимостью.
Она зависит от физических свойств
проводящего материала и температуры,
измеряется в См/м.
Основной
величиной в электрическом поле
проводящей среды является
плотность тока
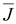 .
Это векторная величина, направленная
по напряженности электрического
поля. .
Это векторная величина, направленная
по напряженности электрического
поля.
Ток
определяют как поток вектора
плотности тока
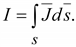 (16.1) (16.1)
Ток
является скалярной алгебраической
величиной.
При
протекании постоянных токов как
внутри проводящих тел, так и вне
их существуют постоянные магнитные
поля. Так как эти поля неизменны
во времени, то в поле явление
электромагнитной индукции
отсутствует. Поэтому электрическое
и магнитное поле постоянного
тока можно рассматривать раздельно.
Магнитные поля постоянного тока
будут рассмотрены в следующей
главе.
|
|
|
|
|
|
Закон
Ома, I, II законы Кирхгофа в
дифференциальной форме
|
|
Выделим
в проводящей среде небольшой
параллелепипед объемом V
(рис. 16.1).
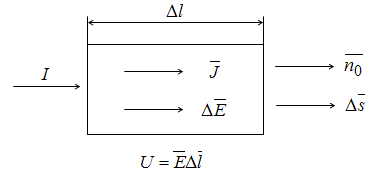
Рис.
16.1. Параллелепипед в проводящей
среде
Длина
ребер параллелепипеда Δl,
площадь поперечного сечения Δs.
Расположим
его так, чтобы напряженность поля
была в нем направлена параллельно
ребру. В силу малости объема можно
считать, что напряженность поля
одна и та же во всем элементарном
объеме:
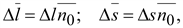
где
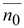 –
единичный вектор по направлению –
единичный вектор по направлению
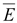 . .
Ток:
 (16.2) (16.2)
Напряжение
на элементе объема:
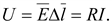 (16.3) (16.3)
Сопротивление
элемента объема:
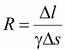 ,
(16.4) ,
(16.4)
где
γ – удельная проводимость среды.
Поставив
в (16.3) выражения (16.2) и (16.4) получим:
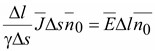 , ,
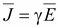 .
(16.5) .
(16.5)
Выражение
(16.5) называют законом Ома в
дифференциальной форме. Это
уравнение справедливо для областей
вне источников ЭДС. В областях,
занятых источниками ЭДС, существует
также так называемое стороннее
электрическое поле, обеспечивающее
непрерывное движение зарядов в
электрической цепи. Это поле
обусловлено химическими,
электрохимическими, тепловыми и
термоэлектрическими процессами.
Закон Ома в дифференциальной форме
для областей, занятых источниками
ЭДС
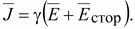 (16.6) (16.6)
Уравнение
(16.6) называется обобщенным законом
Ома. Если от обеих частей взять
интеграл по замкнутому контуру,
то получим второй закон Кирхгофа
в дифференциальной форме.
Если
в проводящей среде выделить
некоторый объем, по которому
протекает постоянный, не изменяющийся
во времени ток, то можно сказать,
что ток, входящий в объем, равняется
току, выходящему из объема, иначе
в этом объеме происходило бы
накопление электрических зарядов,
что опыт не подтверждает. Математически
это записывают так:
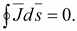 (16.7) (16.7)
Разделим
правую и левую часть уравнения
(16.7) на объем и возьмем предел в
случае, когда объем стремится к
нулю
 (16.8) (16.8)
Соотношение
(16.8) называется первым законом
Кирхгофа в дифференциальной форме.
Он гласит, что в установившемся
режиме (при постоянном токе) в любой
точке тока нет ни истока, ни стока
линий тока проводимости
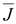 . .
|
|
|
|
|
Уравнение
Лапласа для электрического поля
в проводящей среде
|
|
Так
же, как и в электростатическом
поле, напряженность электрического
поля в проводящей среде:
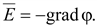
В
неизменном во времени поле:

Если
среда однородна и изотропна, т.е.
γ = const, то можно записать:
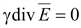 или или
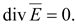
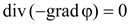
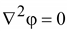 (16.9) (16.9)
Поле
в однородной проводящей среде
подчиняется уравнению Лапласа.
Это
поле является потенциальным, в нем
в областях, не занятых источниками
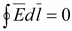 . .
|
|
Переход
тока из среды с проводимостью γ1 в
среду с проводимостью γ2. Граничные
условия
|
|
На
рис.16.2 линия ОО
есть граница раздела сред. Возьмем
на границе раздела плоский замкнутый
контур 1234. Составим циркуляцию
вдоль этого контура. Стороны 12 и
34 его весьма малы по сравнению со
сторонами 23 и 41, длину которых
обозначим dl.
Пренебрежем составляющими интеграла
вдоль коротких сторон
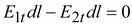 , ,
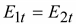 .
(16.10) .
(16.10)
Это
соотношение совпадает с соотношением
(13.23) на границе раздела двух
диэлектриков.

Рис.
16.2. Поле на границе раздела двух
сред
На
границе раздела равны нормальные
составляющие плотностей токов.
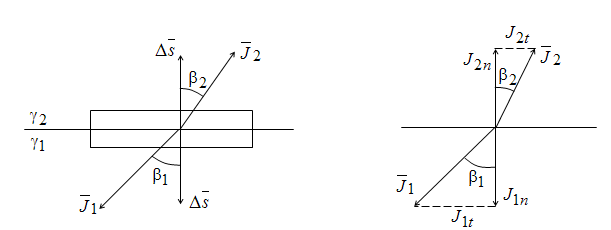
Рис.
16.3. Определение нормальной
составляющей поля
Выделим
на границе раздела сред сплющенный
параллелепипед (рис. 16.3а).
Поток
вектора
 ,
втекающий в объем через нижнюю
грань, равен ,
втекающий в объем через нижнюю
грань, равен
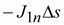 ;
поток вектора ;
поток вектора
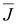 ,
вытекающий из объема через верхнюю
грань – ,
вытекающий из объема через верхнюю
грань –
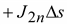 .
Так как .
Так как
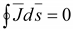 ,
то ,
то
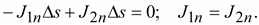 (16.11) (16.11)
Следовательно,
при переходе тока из среды с одной
проводимостью в среду с другой
проводимостью остаются непрерывными
тангенциальная составляющая
вектора напряженности поля
 и
нормальная составляющая плотности
тока и
нормальная составляющая плотности
тока
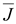 . .
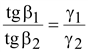 .
(16.12) .
(16.12)
|
Аналогия
между полем в проводящей среде
и электростатическим полем
|
|
По
своей природе электростатическое
поле и поле постоянного тока в
проводящей среде различны.
Электростатическое поле создается
электрическими зарядами,
неизменными во времени и
неподвижными в пространстве.
Электрическое поле в проводящей
среде создается электрическими
зарядами, которые имеют упорядоченное
движение под действием внешнего
источника. Однако между полями
существует формальная аналогия.
Электростатическое
поле в областях, не занятых
зарядами удовлетворяет уравнению
Лапласа. Этому же уравнению
удовлетворяет электрическое
поле постоянного тока в проводящей
среде вне сторонних источников.
В обоих случаях имеют дело с
вектором напряженности
электрического поля
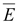 .
Диэлектрической проницаемости
ε соответствует проводимость γ.
С вектором электрического смещения
можно сопоставить вектор плотности
тока .
Диэлектрической проницаемости
ε соответствует проводимость γ.
С вектором электрического смещения
можно сопоставить вектор плотности
тока
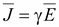 .
С потоком вектора .
С потоком вектора
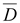 – –
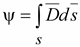 можно
сопоставить поток вектора
плотности электрического тока можно
сопоставить поток вектора
плотности электрического тока
 . .
Граничные
условия на поверхности раздела
двух диэлектриков:
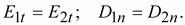
Граничные
условия на поверхности раздела
двух сред с различной проводимостью
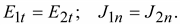
Учитывая
вышесказанное, можно сделать
вывод, что при одинаковой форме
граничных поверхностей картина
поля в обоих случаях будет
одинаковой (совокупность силовых
и эквипотенциальных линий).
|
|
|
|
|
Аналогия
между полем в проводящей среде
и электростатическим полем
|
|
По
своей природе электростатическое
поле и поле постоянного тока в
проводящей среде различны.
Электростатическое поле создается
электрическими зарядами,
неизменными во времени и
неподвижными в пространстве.
Электрическое поле в проводящей
среде создается электрическими
зарядами, которые имеют упорядоченное
движение под действием внешнего
источника. Однако между полями
существует формальная аналогия.
Электростатическое
поле в областях, не занятых
зарядами удовлетворяет уравнению
Лапласа. Этому же уравнению
удовлетворяет электрическое
поле постоянного тока в проводящей
среде вне сторонних источников.
В обоих случаях имеют дело с
вектором напряженности
электрического поля
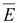 .
Диэлектрической проницаемости
ε соответствует проводимость γ.
С вектором электрического смещения
можно сопоставить вектор плотности
тока .
Диэлектрической проницаемости
ε соответствует проводимость γ.
С вектором электрического смещения
можно сопоставить вектор плотности
тока
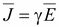 .
С потоком вектора .
С потоком вектора
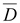 – –
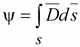 можно
сопоставить поток вектора
плотности электрического тока можно
сопоставить поток вектора
плотности электрического тока
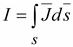 . .
Граничные
условия на поверхности раздела
двух диэлектриков:
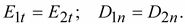
Граничные
условия на поверхности раздела
двух сред с различной проводимостью
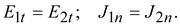
Учитывая
вышесказанное, можно сделать
вывод, что при одинаковой форме
граничных поверхностей картина
поля в обоих случаях будет
одинаковой (совокупность силовых
и эквипотенциальных линий).
|
|
Соотношение
между проводимостью и емкостью
|
|
Если
какие-либо электроды поместить
в проводящую среду и присоединить
к источнику ЭДС, то по проводящей
среде идет ток. Проводимость
между электродами равна

В
свою очередь:
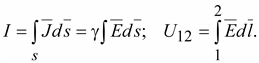
Проводимость
 (16.13) (16.13)
C
другой стороны в электростатическом
поле с электродами такой же
конфигурации емкость между двумя
частями электродов, на которых
расположены одинаковые по величине
и противоположные по знаку заряды
Q
равна:
 (16.14) (16.14)
Учтено,
что
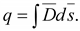
Если
разделить (16.14) на (16.13), то можно
получить:
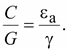 (16.15) (16.15)
Выражение
(16.15) позволяет по известному
выражению емкости между какими-либо
телами получить выражение для
проводимости и наоборот.
Так,
например, емкость двухпроводной
линии:
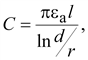 (16.16) (16.16)
где:
l
– длина проводов, d
– расстояние между осями, r
– радиус провода.
Чтобы
получить выражение для проводимости
между двумя параллельными
проводами, погруженными в среду
с проводимостью γ, надо в (16.15)
заменить εa
на γ:
 (16.17) (16.17)
|
|
|
|
|
Общая
характеристика задач расчета
электрического поля в проводящей
среде и методов их решения
|
|
Так
же, как и задачи электростатики,
задачи расчета электрического
поля в проводящей среде можно
классифицировать по характеру
величины, которая определяется
в результате расчета:
1.
На задачи, у которых определяются
точечные характеристики (плотность
тока, потенциал).
2.
На задачи, в которых находят
интегральные характеристики
поля, например, сопротивление
между электродами или напряжение
между какими-то точками.
В
зависимости от того, что задано
и что определяется, все задачи
делятся на два типа:
1.
В первом – заданы форма и
расположение электродов (геометрия
поля), свойства среды и интенсивность
источников, создающих поле.
Требуется найти либо точечные,
либо интегральные характеристики
поля.
2.
Второй тип задачи является
обратным по отношению к первому.
Например: по заданной точечной
характеристике поля, заданным
форме, расположения электродов
и свойствам среды найти интенсивность
источников, создающих поле.
Задачи
расчета электрического поля в
проводящей среде могут быть
решены:
1.
Непосредственным интегрированием
уравнений, описывающих поле.
2.
Использованием аналитических
решений для других статических
невихревых полей.
3.
Экспериментальным или графическим
путем.
4.
Методом зеркальных изображений.
5.
Методом конформных преобразований.
|
|
Связь
основных величин, характеризующих
магнитное поле. Механические
силы в магнитном поле
|
|
Магнитное
поле постоянного тока создается
неизменными во времени токами,
проходящими по проводящим телам,
неподвижным в пространстве по
отношению к наблюдателю.
Электрическое поле постоянного
тока не влияет на магнитное поле,
и их можно рассматривать независимо.
Магнитное
поле характеризуется индукцией
 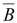 ,
намагниченностью ,
намагниченностью
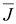 и
напряженностью магнитного поля и
напряженностью магнитного поля
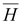 .
Эти три величины связаны
соотношением .
Эти три величины связаны
соотношением
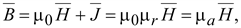 (17.1) (17.1)
где
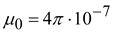 Гн/м
– магнитная постоянная, Гн/м
– магнитная постоянная,
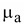 –
абсолютная, а –
абсолютная, а
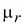 –
относительная магнитная
проницаемость. –
относительная магнитная
проницаемость.
Одним
из основных проявлений магнитного
поля является воздействие его
на проводник с током, помещенный
в это поле. Сила воздействия на
элемент проводника длиной
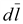
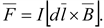 (17.2) (17.2)
Эта
сила перпендикулярна индукции
в данной точке поля и перпендикулярна
элементу с током
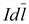 (рис
17.1). (рис
17.1).

Рис.
17.1. Взаимодействие проводника с
током и магнитного поля
Если
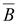 и и
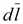 параллельны,
то элемент тока не испытывает
механического воздействия со
стороны магнитного поля. параллельны,
то элемент тока не испытывает
механического воздействия со
стороны магнитного поля.
Механические
воздействия магнитного поля на
ток можно пояснить, исходя из
представлений о деформации
силовых линий магнитного поля
или из понятий о силах Лоренца.

Рис.
17.2. К пояснению воздействия
магнитного поля на проводник с
током
Результирующее
поле слева от проводника разрежено,
а справа – сгущено. Силовые линии
стремятся выпрямиться, производя
давление на провод справа налево.
При
взаимно перпендикулярном
расположении магнитного поля и
провода с током направление
действия силы определяется по
правилу левой руки.
|
|
|
|


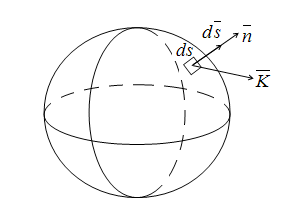
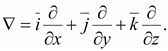
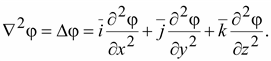 (14.9)
(14.9)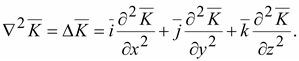 (14.10)
(14.10)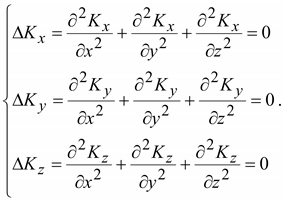 (14.11)
(14.11)
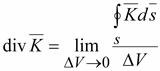 .(14.14)
.(14.14)
 (14.15)
(14.15)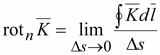 .
(14.16)
.
(14.16)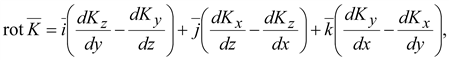 (14.17)
(14.17)
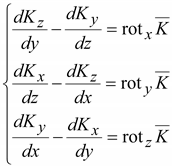 .
(14.18)
.
(14.18)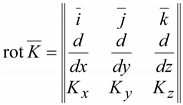 (14.19)
(14.19)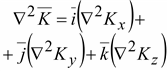
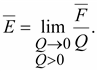 (14.22)
(14.22)
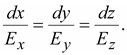 (14.23)
(14.23)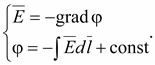 (14.24)
(14.24)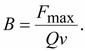 (14.26)
(14.26)
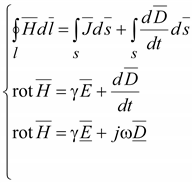 .
(14.37)
.
(14.37)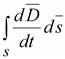 ,
также как и ток проводимости
,
также как и ток проводимости
 (14.38)
(14.38)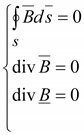 .
(14.39)
.
(14.39)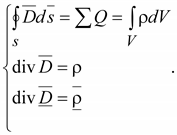 (14.40)
(14.40)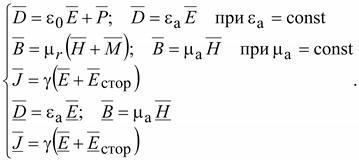 .
(14.41)
.
(14.41)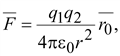 (15.1)
(15.1)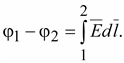 (15.2)
(15.2)
 (15.4)
(15.4) (15.6)
(15.6)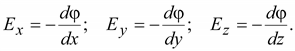 (15.7)
(15.7)
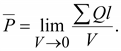 (15.8)
(15.8)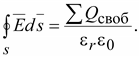 (15.12)
(15.12) .
(15.13)
.
(15.13)
 (15.14)
(15.14)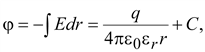 (15.15)
(15.15)
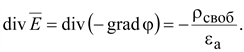
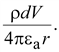
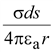 и
и
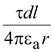 .
.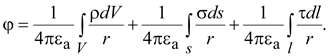 (15.20)
(15.20)

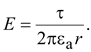 (15.25)
(15.25)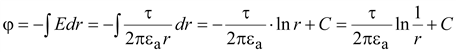 (15.26)
(15.26)
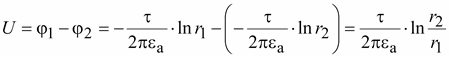 .
.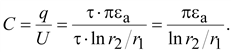 (15.27)
(15.27)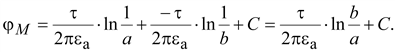 (15.28)
(15.28)

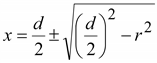 .
(15.29)
.
(15.29)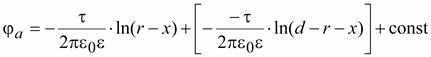 ;
;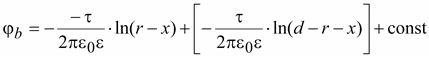 ;
;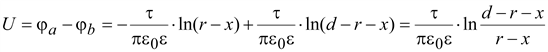 ;
; .
(15.30)
.
(15.30)

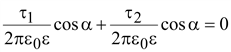 .
.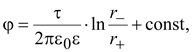 (15.31)
(15.31)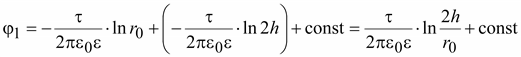 ,
(15.32)
,
(15.32)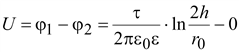 (15.33)
(15.33)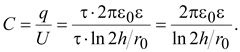 (15.34)
(15.34)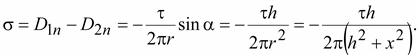 (15.35)
(15.35)

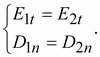
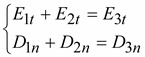 ,
,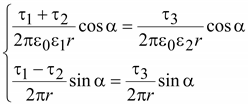 .
.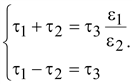
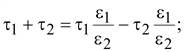
 .
(15.36)
.
(15.36)
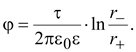
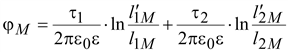
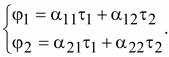 (15.38)
(15.38)
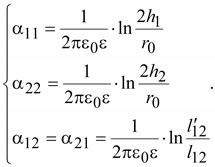 (15.39)
(15.39) (15.40)
(15.40)
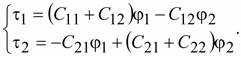 (15.41)
(15.41)

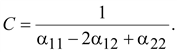 (15.42)
(15.42)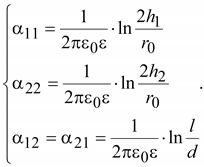
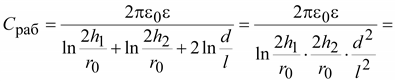
 (15.43)
(15.43) определяет
влияние земли на величину емкости.
определяет
влияние земли на величину емкости.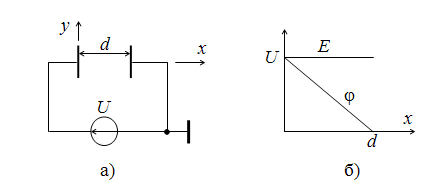
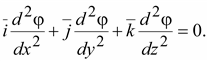

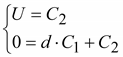 ;
;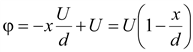 .(15.44)
.(15.44)

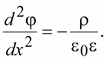 (15.46)
(15.46)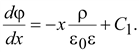
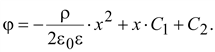 (15.47)
(15.47)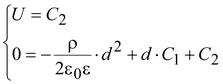 ;
;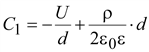
 (15.48)
(15.48) (15.49)
(15.49)
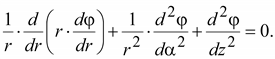 (15.50)
(15.50)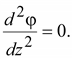
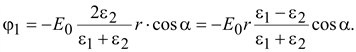 (15.51)
(15.51)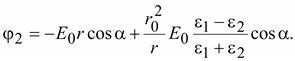 (15.52)
(15.52)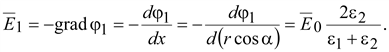 (15.53)
(15.53) (15.54)
(15.54)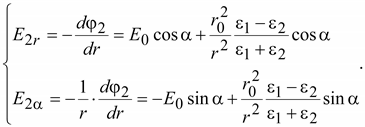 (15.55)
(15.55)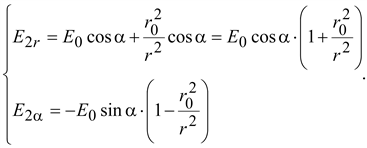 (15.56)
(15.56)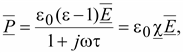 (15.58)
(15.58)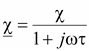 –
комплексная диэлектрическая
восприимчивость, тогда
–
комплексная диэлектрическая
восприимчивость, тогда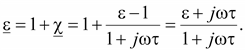 (15.60)
(15.60)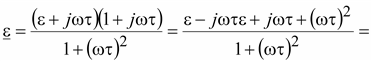
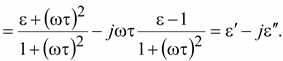
 (15.61)
(15.61)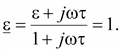 (15.62)
(15.62)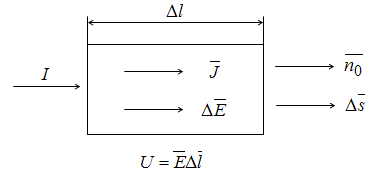
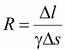 ,
(16.4)
,
(16.4)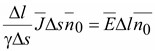 ,
, (16.8)
(16.8)
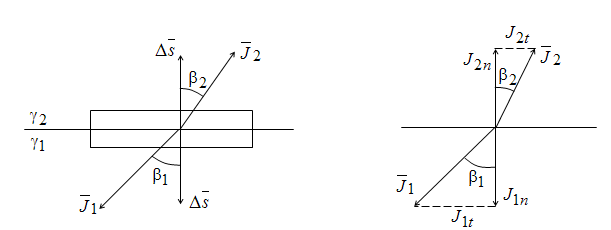
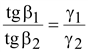 .
(16.12)
.
(16.12)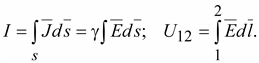
 (16.13)
(16.13) (16.14)
(16.14)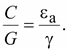 (16.15)
(16.15)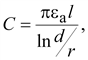 (16.16)
(16.16) (16.17)
(16.17)
