
- •3. Числовые и функциональные ряды
- •3.1. Числовые ряды: основные определения
- •3.2. Простейшие свойства числовых рядов. Необходимый признак сходимости
- •3.3. Признаки сходимости числовых рядов с положительными членами
- •3.4. Знакопеременные ряды. Абсолютная и условная сходимость
- •3.5. Функциональные ряды: основные определения
- •3.6. Степенные ряды
- •3.7. Ряды Тейлора
- •4. Основы теории функций комплексного переменного
- •4.1. Комплексные числа: определение, алгебра комплексных чисел, алгебраическая форма записи
- •4.2. Геометрическое изображение комплексных чисел. Тригонометрическая и показательная формы записи комплексного числа
- •4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа
- •4.4. Функции комплексного переменного
- •1. Показательная функция
- •2. Логарифмическая функция
- •3. Тригонометрические функции
- •4. Гиперболические функции
- •5. Обратные тригонометрические функции
- •6. Общая степенная функция
- •4.5. Дифференцирование функций комплексного переменного. Аналитические функции
- •5. Контрольная работа № 8. Задания
- •5.1. Пример выполнения контрольной работы № 8. Вариант № 0
- •5.2. Варианты заданий контрольной работы № 8
- •Рекомендуемая литература
3. Числовые и функциональные ряды
3.1. Числовые ряды: основные определения
Пусть задана бесконечная последовательность чисел (действительных или комплексных)
![]()
Определение. Числовым рядом называется выражение вида
![]() (1)
(1)
Ряд обозначается:
![]() .
Числа
.
Числа![]() называются членами ряда. Ряд (1) задан,
если известен его общий член
называются членами ряда. Ряд (1) задан,
если известен его общий член![]() ,
т.е. указано правило, по которому каждому
номеру
,
т.е. указано правило, по которому каждому
номеру![]() ставится в соответствие определённое
значение функции
ставится в соответствие определённое
значение функции![]() .
.
Определение.
Сумма
конечного числа
![]() первых членов числового ряда называется
первых членов числового ряда называется![]() -
й частичной суммой, т.е.
-
й частичной суммой, т.е.
![]() .
.
Рассмотрим последовательность частичных сумм числового ряда
![]()
Определение.
Если существует конечный предел
последовательности
![]() частичных сумм, равный
частичных сумм, равный![]() ,
то ряд называется сходящимся, а
,
то ряд называется сходящимся, а![]() называется его суммой:
называется его суммой:
![]() .
.
Если предел
последовательности
![]() не существует или равен бесконечности,
то ряд называется расходящимся.
не существует или равен бесконечности,
то ряд называется расходящимся.
Определение.
Если в ряде (1) отбросить первые
![]() членов, то получится ряд:
членов, то получится ряд:
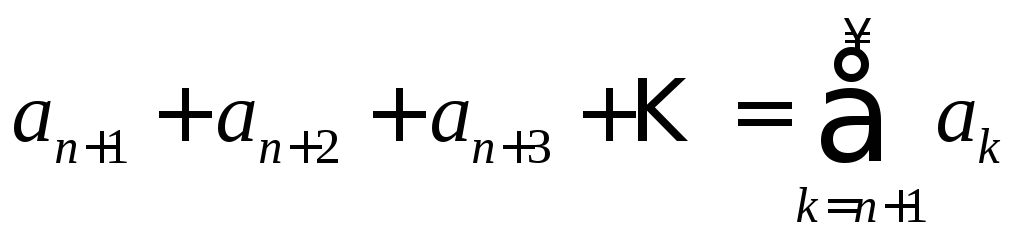 ,
,
называемый остатком ряда (1) .
3.2. Простейшие свойства числовых рядов. Необходимый признак сходимости
Свойства:
Если ряд сходится, то сходится и любой из его остатков. Если сходится какой-либо из остатков ряда, то сходится и сам ряд.
Если числовой ряд
 сходится и его сумма равна
сходится и его сумма равна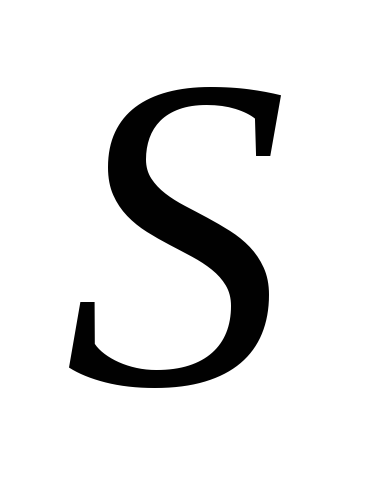 ,
то и ряд
,
то и ряд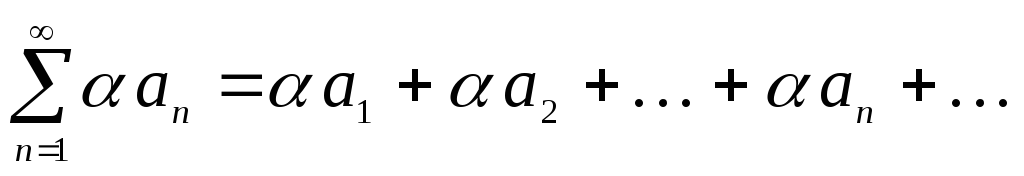 ,
где
,
где – произвольное число, также сходится
и его сумма равна
– произвольное число, также сходится
и его сумма равна .
.Если ряды
 и
и сходятся
и их суммы равны соответственно
сходятся
и их суммы равны соответственно и
и ,
то ряд
,
то ряд также сходится и его сумма равна
также сходится и его сумма равна .
.
Необходимый признак сходимости ряда
Если ряд
![]() сходится, то общий член ряда
сходится, то общий член ряда![]() стремится к нулю при стремлении
стремится к нулю при стремлении![]() к бесконечности, т.е.
к бесконечности, т.е.
![]() .
.
Следствие.
Если общий член ряда
![]() не стремится к нулю при
не стремится к нулю при![]() стремящемся к бесконечности, т.е. если
не выполняется условие
стремящемся к бесконечности, т.е. если
не выполняется условие
![]() ,
,
то ряд расходится.
Замечание.
Условие
![]() является необходимым, но недостаточным,
т.е. если
является необходимым, но недостаточным,
т.е. если![]() ,
то ряд может, как сходится, так и
расходится. Например, ряд
,
то ряд может, как сходится, так и
расходится. Например, ряд![]() расходится, хотя
расходится, хотя![]() .
.
Пример 1. Используя
необходимый признак сходимости, доказать
расходимость ряда
![]() .
.
Решение.
Согласно необходимому условию, если
ряд сходится, то
![]() .
.
Имеем:
![]() .
.
Найдем
![]() :
:
![]()
Так как не выполняется необходимое условие сходимости ряда, то ряд расходится.
3.3. Признаки сходимости числовых рядов с положительными членами
Первый признак сравнения
Пусть
![]() и
и![]() -
ряды с положительными членами, причём
-
ряды с положительными членами, причём![]() при любых
при любых![]() ,
начиная с некоторого
,
начиная с некоторого![]() ,
т.е. для всех
,
т.е. для всех![]() .
Тогда:
.
Тогда:
если ряд
 сходится,
то сходится и ряд
сходится,
то сходится и ряд ;
;Если ряд
 расходится, то расходится и ряд
расходится, то расходится и ряд .
.
Второй признак сравнения
Пусть
![]() и
и![]() -
ряды с положительными членами, причем
существует конечный и отличный от нуля
предел
-
ряды с положительными членами, причем
существует конечный и отличный от нуля
предел
![]() ,
,
Тогда ряды
![]() и
и![]() сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Замечание 1. При использовании 1-го и 2-го признаков сравнения, как правило, сравнивают исходный ряд с рядами, о которых заранее известно, сходятся они или расходятся:
ряд Дирихле
 – сходится при
– сходится при
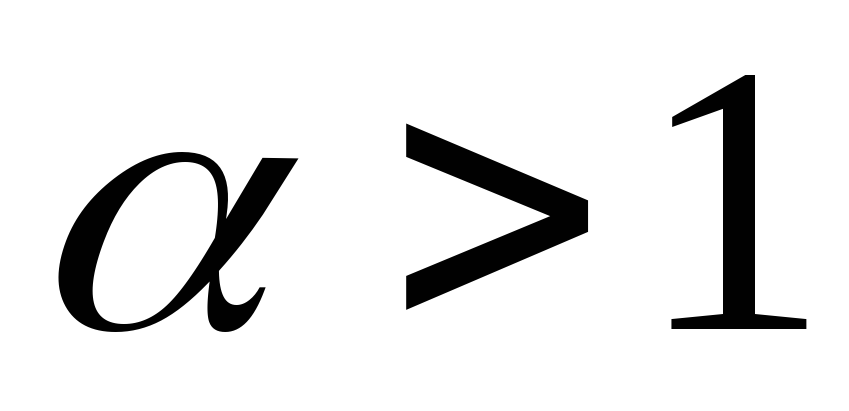 и расходится при
и расходится при .
При
.
При получаем ряд
получаем ряд
 ,
называемый гармоническим.
,
называемый гармоническим.ряд вида
![]() ,
,
члены которого
образуют геометрическую прогрессию со
знаменателем
![]() .
Ряд сходится, если
.
Ряд сходится, если![]() и
расходится при
и
расходится при![]() .
.
Замечание 2. При
отыскании ряда
![]() для сравнения по второму признаку, можно
в общем члене исследуемого ряда заменять
бесконечно малую функцию на эквивалентную
ей функцию, используя основные
эквивалентности бесконечно малых
функций при
для сравнения по второму признаку, можно
в общем члене исследуемого ряда заменять
бесконечно малую функцию на эквивалентную
ей функцию, используя основные
эквивалентности бесконечно малых
функций при![]() :
:
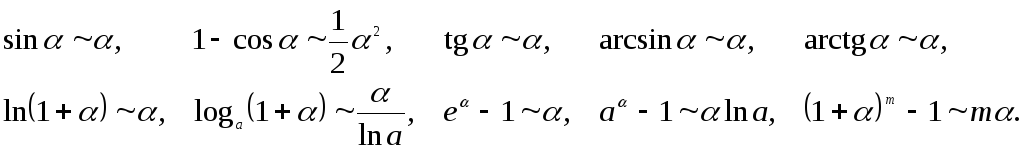
Если в результате
замены мы получим ряд, рассмотренный в
замечании 1, то его можно взять в качестве
ряда
![]() ,
с которым нужно сравнить исследуемый
ряд.
,
с которым нужно сравнить исследуемый
ряд.
Замечание 3. Вопрос о сходимости рядов вида:
![]() ,
,
где
![]() и
и![]() – многочлены степениm
и k,
решается путем сравнения с рядом Дирихле
– многочлены степениm
и k,
решается путем сравнения с рядом Дирихле
![]() ,
где
,
где
![]() .
При этом целесообразно применять второй
признак сравнения.
.
При этом целесообразно применять второй
признак сравнения.
Признак Даламбера
Пусть
![]() –
ряд с положительными членами, и существует
конечный предел
–
ряд с положительными членами, и существует
конечный предел
![]() .
.
Тогда при
![]() ,
данный ряд сходится; при
,
данный ряд сходится; при![]() – расходится.
– расходится.
Радикальный признак Коши
Пусть
![]() –
ряд с положительными членами, и существует
конечный предел
–
ряд с положительными членами, и существует
конечный предел
![]() .
.
Тогда при
![]() ,
данный ряд сходится; при
,
данный ряд сходится; при![]() – расходится.
– расходится.
Замечание 4. Если в признаках Даламбера и Коши предел не существует или равен 1, то ряд может, как сходится, так и расходится. В этом случае требуется исследовать ряд с помощью других методов.
Интегральный признак Коши
Пусть
![]() –
ряд с положительными членами и
–
ряд с положительными членами и![]() положительная, непрерывная и монотонно
убывающая на промежутке
положительная, непрерывная и монотонно
убывающая на промежутке![]() функция такая, что
функция такая, что![]()
Тогда ряд
![]() и несобственный интеграл
и несобственный интеграл![]() сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 2.
Исследовать
сходимость ряда
![]() ,
используя первый признак сравнения.
,
используя первый признак сравнения.
Решение.
Так как
![]() ,
то
,
то![]() ,
,
а ряд
![]() ,
члены которого образуют геометрическую
прогрессию со знаменателем
,
члены которого образуют геометрическую
прогрессию со знаменателем![]() ,
сходится. Тогда на основании первого
признака сравнения, ряд
,
сходится. Тогда на основании первого
признака сравнения, ряд![]() также сходится.
также сходится.
Пример 3. Используя
второй признак сравнения, исследовать
сходимость ряда:
 .
.
Решение.
Имеем:  .
.
Аналогично случаю,
рассмотренному в замечании 3, данный
ряд можно сравнить с рядом
 ,
где
,
где
![]() ;
;![]() ,
который сходится, т.к.
,
который сходится, т.к.![]() .
.
Применим второй признак сравнения. Для этого вычислим:
 .
.
Так как ряд
 сходится, то по второму признаку сравнения
сходится и ряд
сходится, то по второму признаку сравнения
сходится и ряд  .
.
Пример 4. С помощью признака Даламбера исследовать сходимость ряда:
![]() .
.
Решение.
Имеем:
![]()

![]() .
.
Тогда

Следовательно, по признаку Даламбера данный ряд сходится.
Пример 5. С помощью признака Коши исследовать сходимость ряда
![]() .
.
Решение.
Имеем:
![]()
Тогда

Следовательно, по признаку Коши исследуемый ряд расходится.
