Konspekt_lektsy_zm_1_2_3977714072-716176886

9) знайдемо середину відрізка AB– точку M :

x

=

xA + xB

= − 2 + 4

= 1;

y

=

yA + yB

= − 2 +1 = −

1

;

M

M

2

2

2

2

2

y +

1

y − yM

x − xM

x −1

CM :

=

;

2

=

;

y

− y

x

− x

4 +

1

0 −1

C

M

C

M

2

− y −

1

=

9

x −

9

;

y = −

9

x + 4.

2

2

2

2

3. Криві другого порядку

Кривою другого порядку на площині називається множина точок, координати яких у даній декартовій системі координат задовольняють наступному рівнянню

Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 ,

де A2 + B2 + C2 ≠ 0.

Розглянемо найпростіші (канонічні) рівняння кривих другого порядку. 1. Якщо A = C , та B = 0, маємо рівняння кола.

Колом називається множина точок площини, рівновіддалених на величину R, яка має назву радіус, від даної точки O1(a,b), що має назву центру:

(x − a)2 + (y − b)2 = R2 .

Виконаємо тотожні перетворення цього рівняння:

x2 − 2ax + a2 + y2 − 2by + b2 − R2 = 0; x2 + y2 + lx + my + n = 0.

Тут: l = −2a ; m = −2b; n = a2 + b2 − R2 .

Якщо l2 + m2 − 4n > 0

, матимемо рівняння дійсного кола;

якщо l

2

+ m

2

− 4n = 0, маємо точку O

−

l

;−

m

або R = 0;

1

2

2

якщо l2 + m2 − 4n < 0

, маємо уявне коло.

11

Приклад. Знайти координати центру O1 і радіус ( R ) кола:

a)x2 − 2x + y2 + 4y +1 = 0;

b)x2 + 3x + y2 + y + 2 = 0.

Розв’язання. Треба виділити повні квадрати: (a ± b)2 = a2 ± 2ab + b2 ;

a) x2 − 2x +1−1+ y2 + 4y + 4 − 4 +1 = 0,

14243 14243

(x −1)2 + (y + 2)2									= 22 ; O (1;−2);											R = 2;
														1
b) x	2 + 2 3 x +					9 −	9 + y2 + 2							1 y +				1	−	1		+		8	= 0,
		2				4	4							2				4		4				4
1442443										1442443
		3					1									2					3				1
				2						2																	2
													2						(−				;−			) ; R =
	(x +		)		+	(y +			)		=						; O1													.
		2					2					2									2				2		2

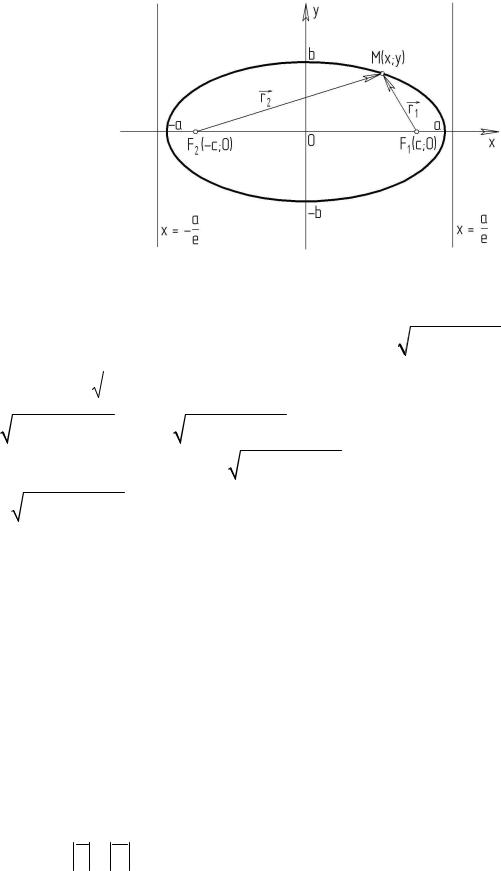
2. Еліпсом називається множина точок площини, сума відстаней яких від двох даних точок, що мають назву фокусів, стала (рівна 2а), що менша ніж відстань між фокусами (2с).

Якщо розташувати декартову систему координат таким чином, що вісь

ОХ проходитиме через фокуси			F1F2 ,				а вісь OY посередині між ними
(рис. 3), то рівняння
		x2	+	y	2		= 1
		a2		b	2

має назву канонічного рівняння. Числа 2а і 2b представляють довжини великої і малої осей еліпса. Вони зв’язані наступним співвідношенням:

с2 = a2 − b2 .

Точки (a,0); (−a,0) ; (0,b); (0,−b) мають назви вершин еліпса. Відношення половини фокальної відстані до половини великої осі

називається ексцентриситетом еліпса e = c . a

Ексцентриситет характеризує степінь стискання еліпса, і для еліпсу e < 1. Для кола e =1.

12

Рис. 3

Отримаємо канонічне рівняння еліпсу:

За означенням:

+

= 2a > 2c, де

= MF = (x − c) + y2

;

r

r

r

1

2

1

1

= MF = (x + c) + y2

r

2

1

(x + c)2 + y2 = 2a − (x − c)2 + y2

x2 + 2cx + c2 + y2 =4a2 − 4a (x − c)2 + y2 + x2 − 2cx + c2 + y2 ; a(x − c)2 + y2 =a2 − cx;

a2 x2 − 2a2cx + a2c2 + a2 y2 =a4 − 2a2cx + c2 x2 ; (a2 − c2 )x2 + a2 y2 = a2 (a2 − c2 );

	Так як a > c , то a2	− c2 > 0.
	Позначимо b2 = a2	− c2 , тоді b2 x2 + a2 y2 = a2b2 або	x2		+	y	2	=1.
			a	2		b	2

3. Гіперболою називається множина точок площини, модуль різниці яких від двох даних точок, що мають назву фокусів, є величина стала (що дорівнює 2а), менша ніж відстань між фокусами (2с).

Якщо розташувати декартову систему координат аналогічно попередньому випадку (рис. 4) і виконати відповідні тотожні перетворення

виразу: r1 − r2 = 2a > 2c , то отримаємо канонічне рівняння гіперболи

	x	2	−	y	2	= 1	.
	a	2		b	2

13

Числа 2а і 2b являють собою довжини дійсної і уявної осей гіперболи. Вони зв’язані наступним співвідношенням: с2 = a2 + b2 .

Точки (a,0) і (−a,0) мають назву вершини гіпербол. Відношення половини фокальної відстані до половини довжини дійсної осі має назву

ексцентриситету гіперболи: e = c . a

y = ab x

y = − ab x

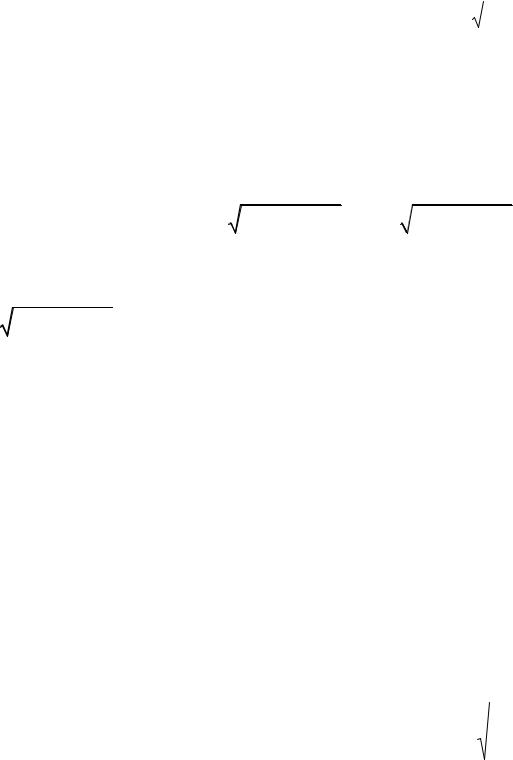
Рис. 4

Для гіперболи e > 1.

Прямі y = ± b x мають назву асимптот гіперболи. Якщо a = b, a

гіпербола має назву рівнобічної.

Має місце так звана фокально-директоріальна властивість кривих другого порядку, за якою відношення відстаней від будь-якої точки M (x; y) кривої до фокуса і відповідної директриси є стале, що дорівнює

			→
			rM			= e .
ексцентриситету кривої:
			dM

Користуючись фокально-директоріальною властивістю кривих другого порядку, отримаємо канонічне рівняння гіперболи.

14

			→
			rM				→
Розглянемо рівність						= e (рис. 4), де		= MF = (x + c)+ y2		;
							r
			dM				1	1

d1 – це відстань від точки M (x; y) до правої директриси гіперболи, що має

рівняння x =	a	або у загальному вигляді x −			a	= 0.
	e				e
Вважаючи, що e =			c	, рівняння правої директриси має вигляд x −			a2	= 0.
							c
			a

Тоді d =

x −

a

2

(x − c2 ) + y2

c

c (x − c2 ) + y

2

c

і матимемо

=

;

=

;

1

c

a

2

a

cx

− a

2

a

x −

c

a (x − c)2 + y2 =

cx − a2

;

Піднесемо до квадрату обидві частини рівняння:

a2 x2 − 2a2 xc + a2c2 + a2 y2 = c2 x2 − 2cxa2 + a4;

x2 (c2 − a2 ) − a2 y2 = a2 (c2 − a2 );

Оскільки c > a, то c2 − a2 > 0.

Позначимо b2 = c2 − a2 , тоді b2 x2 − a2 y

2 = a2b2

або

x2

−

y2

=1.

a

2

b

2

4. Параболою називається множина точок площини, рівновіддалених

від даної точки – фокуса і від даної прямої – директриси.

Розташувавши декартову систему координат, як зображено на рис. 5,

отримаємо наступне канонічне рівняння параболи:

y2 = 2px

,

де

p – параметр

параболи,

що

чисельно

дорівнює

відстані

між

p

p 2

+ y2

фокусом і директрисою.

r

= d ;

r

= x +

.

Тут

r

=

x −

2

2

Директриса має рівняння

x = −

p

;

2

15

Рис. 5 Зауважимо, що поняття директриси притаманне також еліпсу і

гіперболі, що мають по дві директриси, рівняння яких x = ± a . e

Ці лінії перпендикулярні фокальній осі й розташовані зовні від вершини у випадку еліпса (е <1 x > a ) і між вершинами у випадку гіперболи (е > 1 x < a ). Так, права директриса відповідає правому фокусу, а ліва – лівому.

Приклад. Скласти рівняння парабол:

a)точка A(1;2) належить параболі; OX являє собою вісь симетрії;

b)рівняння директриси параболи y = −2.

Розв’язання.

a) y2 = 2px; 22 = 2p 1; p = 2;

y2 = 4x ;

b) y = −2; −

p

= −2; p = 4; x2

= 2py ; x2 = 8y .

2

Приклад. Скласти рівняння еліпсів: a) точки A(0;−2) і

15

лежать

B

2

на еліпсі;

b) точка A(0;

5

.

11) є вершиною і е =

6

16

Розв’язання.

a)

x2

+

y2

= 1;

щоб

знайти a2 і b2

підставимо у

a2

b2

рівняння відповідні координати точок A і B .

0

(−2)2

А:

+

= 1;

;

a2

b2

B :

15

+

1

= 1;

4a2

b2

Розв’яжемо систему і знайдемо a2

і b2 . З першого рівняння b2

= 4,

З другого рівняння

15

+

1

=

4

;

а2 = 5;

4a2

4

4

Отже,

x2

+

y2

= 1;

x2

+

y2

= 1.

5

4

(

5)2

(2)2

b)

x2

+

y2

= 1;

0

+

11

= 1; b2 = 11

a2

b2

a2

b2

е =

с

=

5

;

с

2

= a

2

− b

2

;

a2

− b2

=

25

;

36

−

11

=

25

;

а

6

a2

36

36

a2

36

11

= 11

;

a2 = 36;

x2

+

y2

= 1;

x2

+

y2

= 1.

36

a2

36

11

62

( 11)2

Приклад. Скласти рівняння гіпербол:

a) точки A(3;4) та B(5;45) лежать на гіперболі;

b) точка A(6;0) є вершиною і k =

2

.

2

Розв’язання. a)

x2

−

y2

= 1;

Розв’язуємо аналогічно попередньому

2

a

b

2

прикладу.

А:

9

− 16 = 1

–5

a2

b2

+

B : 25 − 80 = 1 a2 b2

Перше рівняння помножили на -5 і склали з другим. Отримали:

17

− 45

+

25

+

80

−

80

= −5 +1;

− 20

= −4; a2 = 5;

a

2

а

2

b

2

b

2

a

2

25

− 80

= 1;

80

= 4; b2 = 20;

x2

−

y2

= 1;

x2

−

y2

=1;

b2

5

b2

5

20

( 5)2

(2 5)2

x2

y2

b)

−

= 1; a = 6; k = b / a =

2

/ 2;

2

a

b

2

x2

2

b =

2

a =

2

6

=

−

y

= 1.

3 2 ;

2

2

62

(3

2)2

4. Полярна система координат

Полярна система координат задається точкою О, що має назву полюс, і полярною віссю або полярою ОР (рис. 6) з одиницею вимірювання або масштабом.

y						M(ρ; φ)
y
		ρ
		φ				P
					x	x
0	1	2		3
		Рис. 6

Положення точки М визначається числами ρ і ϕ , де ρ відстань її від полюса, ϕ – кут між відрізком ОМ і полярною віссю (відлік кутів ведеться від полярної осі проти годинникової стрілки).

Числа ρ і ϕ мають назву полярних координат точки М: ρ – полярний

радіус, ϕ	– полярний кут. Між множиною усіх	точок площини (крім
точки О )	і множиною впорядкованих пар чисел	(ρ;ϕ), де ρ ≥ 0 і
ϕ [−π;π ]	(або 0 ≤ ϕ < 2π ), існує взаємно однозначна відповідність. Для

точки О величина полярного кута не визначена.

18

Встановимо зв'язок між прямокутними й полярними координатами. Якщо за полюс взяти початок прямокутної системи координат, а за полярну вісь – додатний напрям осі OX (рис. 6), прямокутні координати x і y точки М і її полярні координати ρ і ϕ , окрім полюса, зв’язані наступними формулами:

	x = ρ cosϕ			ρ = x2 + y2
						y
	y = ρ sinϕ	;		tgϕ =					.
						x

					π
	Приклад. Знайти прямокутні координати точки		2;				і полярні
		A			4

координати точки B(−1;3), якщо полюс співпадає з початком декартової

системи координат, а полярна вісь з додатнім напрямом осі OX.

Розв’язання.

cos π

1

π

1

x = ρ cosϕ =

2

=

2

=1; y = ρ sinϕ = 2 sin

=

2

=1;

4

4

2

2

π

2;

Таким чином точка A

4

має декартові координати A(1;1).

Точка B лежить у другій чверті,

= (−1)2 + (

)2 =

= 2;

ρ =

x2 + y2

3

4

2π

tgϕ =

3

= −

3; звідси ϕ =

+ 2π n , де n Ζ.

3

−1

2π

Таким чином точка B(−1;

3) має полярні координати

B 2;

.

3

Приклад. Побудувати в полярній системі координат криву, яка має назву «лемніската Бернуллі»: (x2 + y2 )2 − a2 (x2 − y2 ) = 0, (a > 0).

Розв’язання. Перейдемо до полярних координат:

(ρ2 cos2 ϕ + ρ2 sin2 ϕ)2 =a2 (ρ2 cos2 ϕ − ρ2 sin2 ϕ) або ρ2 = a2 cos2ϕ .

Звідси ρ = ±acos2ϕ . Знак «±» вказує на той факт, що крива симетрична відносно полюса. Область допустимих (можливих) значень кута ϕ

19

знаходимо з нерівності: cos2ϕ ≥ 0; −π4 + kπ ≤ ϕ ≤ π4 + kπ , k Ζ. Оскільки

cos2ϕ – парна функція, то крива буде симетрична відносно полярної осі. Таким чином достатньо побудувати криву в першій чверті і

скористатися умовами симетрії.

Для першої чверті 0 ≤ ϕ ≤

π

з кроком

π

сформуємо таблицю:

4

16

ϕ

0

π

π

3π

π

16

8

16

4

ρ

a

≈ 0,96a

≈ 0,84a

≈ 0,62a

0

Отже, ρ спадає від a до 0. Будуємо лемніскату Бернуллі (рис.7).

	π
y	4		3π
			16	π
				8
				π
				16
			a	x

0

Рис. 7

20