Lektsii_Mekhanika_Ch_1

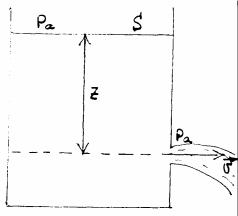
В установившемся потоке невязкой жидкости выделим участок трубки тока (рис.75). Высоты центров сечений, давление, удельный вес, скорость жидкости для левого и правого сечений равны

z1, p1,γ1,ν1

и:

z2 , p2 ,γ 2 ,ν2

Если весовой расход в левом сечении участка трубки тока равен θ1 , то в единицу времени в выделенный участок втекающей жидкостью вносится энергия:

p

ν 2

z

+

1

+

1

θ

1

1

γ1

2g

Одновременно в единицу времени через правое сечение из трубки тока удаляется

энергия:

p

2

ν

2

z

+

+

2

θ

2

2

γ 2

2g

При установившемся потоке невязкой жидкости полная энергия жидкости в участке

трубки тока не изменяется, т.е.:

p

ν 2

p

2

ν

2

z +

1

+

1

θ

=

z

+

+

2

θ

(294)

1

2

2

1

γ1

γ 2

2g

2g

Учитывая, что, по уравнению неразрывности струи:

θ1 = θ2

получим окончательно математическую формулировку закона Бернулли:

p

ν 2

z +

+

= const

γ

2g

(295) Физически закон Бернулли (уравнение Бернулли) имеет смысл закона сохранения

энергии с учетом закона сохранения массы.

15.10.Примеры применения закона Бернулли

15.10.1.Формула Торичелли

(рис. 76)

Формула Торричелли позволяет определить скорость истечения жидкости из отверстия в сосуде. Предположим, что в широкий сосуд площади сечения S налита жидкость, свободная поверхность которой находится на высоте Z над центром малого отверстия площади в боковой стенке сосуда (рис.76). Давление на свободной поверхности жидкости и в вытекающей струе непосредственно за отверстием равно атмосферному Ра.

Пусть скорость истечения жидкости равнаν , а скорость понижения уровня жидкости в сосуде - ν 0 . Жидкость будем считать несжимаемой.

Запишем уравнение Бернулли, сравнивая сечение для свободной поверхности жидкости с сечением отверстия:

z +	pa	+ ν02	= z +	pa	+	ν 2
	γ 2g			γ 2g

Т.к. площадь сечения отверстия мала по сравнению с сечением сосуда, а жидкость несжимаема, то:

ν >>ν0

откуда следует формула Торричелли:

ν = 2gz

(296)

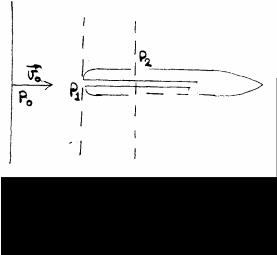
15.10.2 Трубка Пито

(рис. 77)

Трубка Пито служит для определения скорости потока жидкости и давления в нем. Она представляет собой осесимметричное тело с центральным отверстием и наборов боковых (рис.77). Центральное отверстие имеет непосредственный выход из трубки, а боковые - соединены с плоскостью трубки, которая также имеет выход наружу. Поперечные размеры трубки малы по сравнению с размерами потока. Выделим в потоке жидкости обтекающем трубку, три течения: в невозмущенной части потока, у центрального и боковых отверстий поток, набегая на трубку, тормозится у центрального отверстия, скорость его становится равной нулю, а давление у центрального отверстия P1 будет отличаться от давления Р0 в невозмущенной части потока. У боковых отверстий скорость жидкости практически такая же как в невозмущенной части потока V0, а давление равно P2. Считая жидкость невязкой и несжимаемой, запишем уравнение Бернулли для сечений в невозмущенной части потока и у центрального отверстия:

	p		+	ν	2	=		p
	0				0			1
	γ			2g				γ
откуда:
p1		= p0 +					ρν 2
								0
								2

Сравнивая сечение потока в невозмущенной части с сечением у боковых отверстий и пренебрегая поперечными размерами трубки, получим:

p	+	ν	2	=	p	2	+	ν	2
0			0						0
γ		2g			γ			2g

Т.е. давление у боковых отверстий равно давлению в невозмущенной части потока: p2 = p0

Т.е., измеряя давление в полости трубки и у центрального отверстия, можно определить и давление, и скорость в потоке жидкости.

15.11. Реакция струи жидкости

Рассмотрим рис.78. В результате действия на поток внешних сил на выделенном

участке происходит изменение импульса K, равное:
k = ρSν (ν 2 −ν1 )= F	(297)

(рис. 78)

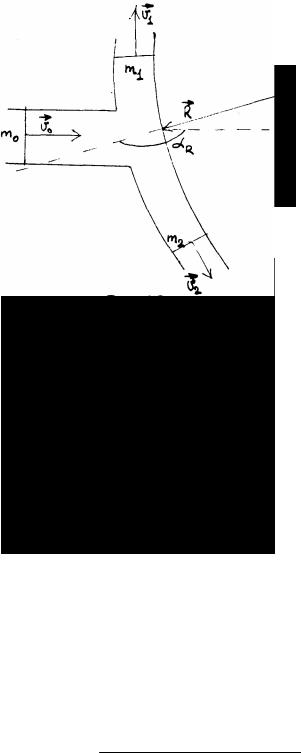
Рассмотрим теперь поток жидкости набегающей на преграду и разветвляющийся на два рукава (рис.79):

(рис. 79)

Пусть массовый расход в неразветвленной части равен m0, а скорость в этом сечении равна V0. Попадая на преграду, поток изменяет импульс в результата действия сил со стороны преграды, выделим сечения в рукавах разветвленной части потока. В которых массовые расходы равны, соответственно m1 и m2 , скорости V1 и V2, причем векторы скоростей образуют углы α1 и α2 с направлением скорости в неразветвленной части потока. Сила R действующая со стороны преграды на поток, образует угол αR с вектором скорости V0 . По (297) изменение импульса потока равно в единицу времени равно:

m1ν1 cosα1 + m2ν2 cosα2 − m0ν0

откуда сила:

R = m1ν1 cosα1 + m2ν2 cosα2 − m0ν0
cosαR	(298)

В случае симметричной преграды массовые расходы в рукавах разветвленной части одинаковы и равны:

m1 = m2 = m0

2

Скорость жидкости в рукавах в этом случае равна скорости в неразветвленной части, а углы α2=α1=α.

Реакция преграды направлена противоположно потоку (αR =π). Следовательно:

R = m0v0	− m1ν1 cosα − m2ν2	cosα = m0ν0	(1− cosα)
			(299)

Как видно из этого результата, максимальной реакция преграды будет в том случае, если скорости в рукавах противоположны скорости в неразветвленной части потока (α =π). Тогда

R = m0v0	(1+1) = 2m0ν0	(300)

15.12. Ламинарное и турбулентное течение жидкости. число Рейнольдса.

Ламинарным называют упорядоченное, слоистое течение жидкости. Моделью такого течения является относительное движение звеньев телескопической антенны. Ламинарное течение возможно в жидкостях при относительно малых скоростях потока, если же скорость потока увеличивать, то в нем возникают вихри. Когда вихри занимают весь объем потока, последний называется вихревым или турбулентным. Образование вихрей связано с взаимодействием частиц слоев жидкости и переносом импульса из слоя в слой. Переносу содействуют силы инерции, а препятствуют - силы вязкого трения. Поэтому критерием перехода от ламинарного течения к турбулентному может служить отношение этих сил. В общем случае, независимо от формы потока, следует рассматривать некоторые характеристические параметры потока, например, характеристические размеры и т.д. Силу вязкого трения можно выражать из закона Ньютона для вязкого трения, а силу инерции - по определению:

	=	F	=	ρl3vtl	=	ρlv
R		ин
				tµl2 l		µ
e		F
		тр					(301)

Полученное выражение называется числом (критерием) Рейнольдса. Вводя понятие кинематической вязкости, число Рейнольдса можно записать и так:

				R	=	lv
				e		η
								(302)
где	-	η =	µ	кинематическая вязкость жидкости.
			ρ

15.13. Формула Пуазейля

(рис. 80)

Формула Пуазейля дает величину объемного расхода жидкости при ламинарном течении жидкости по цилиндрическим трубам. Рассмотрим установившийся поток

жидкости по цилиндрической трубе радиуса R и длины L, ось которой горизонтальна (рис.80). Давление в левом сечении трубы равно P1, а в правом Р2, причем P1>P2. Скорость потока максимальна вдоль оси трубы и равна ну ли у стенок, выделим в трубе тонкий цилиндрический слой радиуса х и толщины dx, в пределах которого скорость жидкости можно считать одинаковой. На торцы выделенного слоя действует силы давления, равнодействующая которых равна:

(p1 − p2 ) 2πxdx

На внутреннюю и внешнюю поверхности слоя действуют силы вязкого трения. По закону Ньютона для вязкого трения на внутреннюю поверхность слоя действует сила:

Fтр = µ 2πxL dv dx

а равнодействующая сил вязкого трения, приложенных к внутренней и внешней поверхностям, соответственно равна:

		dv
dFтр	= µ 2πxLd x
		dx

Так как жидкость движется с постоянной скоростью, сумма приложенных к слою сил равна нулю, т.е.:

					dv
( p1	− p2 ) 2πxdx = −2πµLd x
					dx		(303)
Интегрируя (303), получим:
	( p1 − p2 )	x2 = −x	dv	+ C
	2Lµ		dx	1

Постоянную интегрирования С1 можно получить из условия, что вдоль оси трубы скорость максимальна:

x = 0, dv = 0 dx

	следовательно С1=0. С учетом этого:
	dv = −	( p1 − p2 )	xdx
		4Lµ
			(304)

Интегрируя (304), получим:
v = −	( p1 − p2 )	x2 + C
			2
	4Lµ

Постоянную интегрирования С2 получим из условия, что у стенок трубы скорость жидкости равна нулю x=R, V=0, поэтому:

C2 = ( p1 −µp2 ) R2

4L

Подставив найденное значение постоянной интегрирования в общее решение, получим зависимость скорости жидкости от расстояния до оси трубы:

		v =	p1 − p2	(R2		− x2 )
			4Lµ					(305)
Для определения объемного расхода запишем сначала элементарный объемный
расход по выделенному цилиндрическому слою:
dV = vdS =	p1 − p2	(R2 − x2 ) 2πxdx =			π ( p1 − p2 )		(R2	− x2 ) xdx
	4Lµ
						2Lµ

(306) Полный объемный расход по всей трубе получим интегрированием (306) по всем

слоям:

R	π (p	− p	2	)		x2		R		x4		R		π ( p	− p	2	)R4
V = ∫dV =	1				R2				−				=	1
	2Lµ														8Lµ
						2				4
0								0				0					(307)

Выражение (307) называет формулой Пуазейля.