
- •Дифференциальное исчисление Лекция № 18. Тема 4 : Производная и дифференциал
- •4.1. Производная функции
- •4.2. Производные основных элементарных функций
- •4.3. Механический смысл производной
- •4.4. Геометрический смысл производной
- •4.5. Правила дифференцирования
- •4.6. Производная сложной функции
- •Лекция № 19.
- •4.7. Производная обратной функции
- •4.8. Производная функции, заданной параметрическими уравнениями
- •4.12. Дифференциал функции
- •5.2. Теорема Лагранжа
- •5.4. Формула Тейлора
- •Лекция № 21. Тема 6 : Исследование поведения функций
- •6.1. Возрастание и убывание функций
- •6.2. Экстремум функции. Необходимое условие
- •6.3. Достаточные условия экстремума
- •6.4. Наибольшее и наименьшее значения функции на отрезке
- •Лекция № 22.
- •6.5. Выпуклость, вогнутость, точки перегиба
- •6.6. Асимптоты линий
- •6.7. Общий план исследования функций и построение графиков
- •Лекция № 23.
- •6.8*. Кривизна кривой
- •С о д е р ж а н и е
6.3. Достаточные условия экстремума
Так как точка максимума разделяет интервалы возрастания и убывания, а точка минимума убывания и возрастания, то получаем
Первое достаточное
условие экстремума.
Если при переходе через критическую
точку слева направо производная меняет
знак с плюса на минус, то это точка
![]() Если – с минуса на плюс, то это точка
Если – с минуса на плюс, то это точка
![]()
Второе достаточное
условие экстремума.
Пусть точка х0
является стационарной точкой функции
![]() ,
которая имеет непрерывную произ-водную
второго порядка в окрестности этой
точки. Тогда, если
,
которая имеет непрерывную произ-водную
второго порядка в окрестности этой
точки. Тогда, если![]() ,
то точках0
– точка
,
то точках0
– точка
![]() если
если
![]() ,
то
,
то
![]()
Действительно,
запишем для функции
![]() формулу Тейлора при
формулу Тейлора при![]() в окрестности точких0:
в окрестности точких0:

Так как точка х0
является стационарной точкой функции
![]() ,
то
,
то![]() и из формулы Тейлора следует
и из формулы Тейлора следует
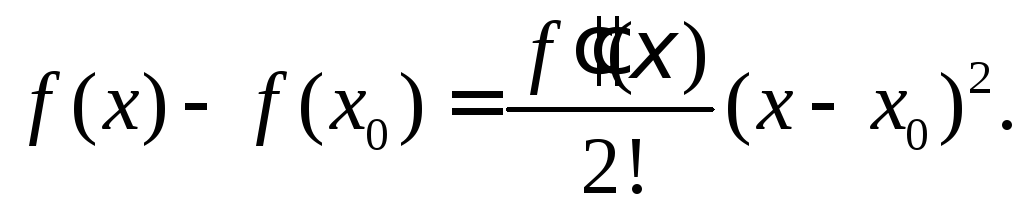
Отсюда в силу
непрерывности
![]() имеем:
имеем:
1.
Если
![]()
2.
Если
![]()
Пример 2.
Исследовать на экстремум функцию
![]() .
.
Найдём производную данной функции
![]() ,
,
из которой
определим критические точки:
![]() .
.
Построим таблицу
|
х |
|
1 |
|
2 |
|
3 |
|
|
|
|
|
+ |
0 |
|
|
+ |
|
у |
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Итак, функция
![]() имеет экстремум (максимум), равный
имеет экстремум (максимум), равный![]() в точке
в точке![]() и два экстремума (минимума), равных0,
в точках
и два экстремума (минимума), равных0,
в точках
![]() Или сокращенно:
Или сокращенно:![]()
6.4. Наибольшее и наименьшее значения функции на отрезке
Пусть задана
непрерывная на
![]() функция
функция![]() .
Она достигает своих наибольшего и
наименьшего значений либо во внутренних
крити-ческих точках
либо
на
концах
отрезка
.
Она достигает своих наибольшего и
наименьшего значений либо во внутренних
крити-ческих точках
либо
на
концах
отрезка
![]() .
Отсюда
следует
.
Отсюда
следует
Правило.
Для того, чтобы найти наибольшее
(наименьшее) значение
![]() на
на
![]() необходимо:
необходимо:
1. Найти
критические
точки,
принадлежащие
данному
отрезку
![]() ;
;
2. Вычислить значения
функции
![]() в критических точках и на концах отрезка
в критических точках и на концах отрезка![]() ;
;
3. Выбрать из полученных значений наибольшее и наименьшее.
Пример 3. Найти наибольшее и наименьшее значения функции
![]() на
отрезке
на
отрезке
![]() .
.
Находим критические точки
![]() .
.
Вычисляем значения
функции в критической точке х
= 1
и на кон-цах рассматриваемого отрезка
![]() :
:
![]()
П ример
4.* Из круглого
бревна, диаметр которого равен d,
требуется вырезать балку прямоугольного
поперечного сечения. Каковы должны быть
ширина и высота этого сечения, чтобы
балка оказывала наибольшее сопротивление
на изгиб, если сопротивление на изгиб
вычисляется по формуле
ример
4.* Из круглого
бревна, диаметр которого равен d,
требуется вырезать балку прямоугольного
поперечного сечения. Каковы должны быть
ширина и высота этого сечения, чтобы
балка оказывала наибольшее сопротивление
на изгиб, если сопротивление на изгиб
вычисляется по формуле
![]() ,
гдеk
упругая постоянная, a
ширина, h
высота сечения балки.
а
,
гдеk
упругая постоянная, a
ширина, h
высота сечения балки.
а
Обозначим
![]() .
.
Тогда
![]() и
и
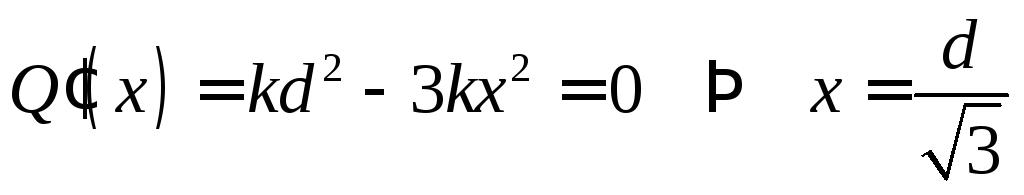 h
h
Покажем, что это точка максимума,
воспользовавшись вторым достаточным
условием экстремума
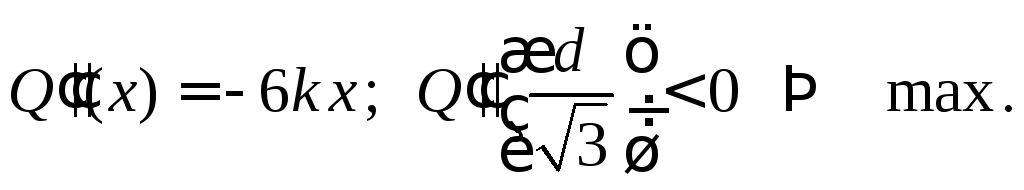
Лекция № 22.
6.5. Выпуклость, вогнутость, точки перегиба
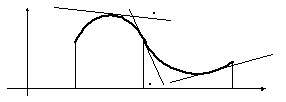
Определение 1.
Линия
![]() называется выпуклой (вогнутой) на
называется выпуклой (вогнутой) на![]() ,
если все точки линии, кроме точки касания,
лежат ниже (выше) любой её касательной
на этом интервале. Точка, отделяющая
выпуклую часть графика от вогнутой,
называется точкой перегиба.
,
если все точки линии, кроме точки касания,
лежат ниже (выше) любой её касательной
на этом интервале. Точка, отделяющая
выпуклую часть графика от вогнутой,
называется точкой перегиба.
y
![]()
О а х0 b x
Здесь на интервале
![]() функция
функция![]() выпукла, на интервале
выпукла, на интервале![]() функция
функция![]() вогнута,х0
точка перегиба.
вогнута,х0
точка перегиба.
Для определения интервалов выпуклости (вогнутости) используется условие их существования.
Теорема 1.
Если для
![]() ,
то на этом интервале линия выпукла
(вогнута).
,
то на этом интервале линия выпукла
(вогнута).
Пусть
![]() .
Уравнение касательной, проведённой в
точке
.
Уравнение касательной, проведённой в
точке![]() ,
имеет вид
,
имеет вид![]() ,
а уравнение линии
,
а уравнение линии![]() .
Рассмотрим разность
.
Рассмотрим разность
![]() .
(1)
.
(1)
К первым двум
членам правой части выражения (1) применим
теорему Лагранжа и рассмотрим случай
![]()
![]() .
.
Ещё раз воспользуемся теоремой Лагранжа
![]() .
.
В этом случае
![]() ,
а это означает, что на интервале
,
а это означает, что на интервале![]() линия
линия![]() выпукла.
выпукла.
Аналогично теорема
доказывается и для случая
![]() .
.
Точно также можно доказать условие вогнутости.
Из определения точки перегиба следует:
Необходимое
условие точки перегиба.
Если х0
точка перегиба функ-ции
![]() ,
то в этой точке
,
то в этой точке![]() либо не существует.
либо не существует.
С учетом теоремы об условиях выпуклости (вогнутости) получаем
Достаточное
условие точки перегиба.
Если
![]() или не существует и при переходе через
эту точку
или не существует и при переходе через
эту точку![]() меняет знак, то точках0
является точкой перегиба.
меняет знак, то точках0
является точкой перегиба.
Пример 1.
Найти интервалы выпуклости, вогнутости,
точки перегиба функции
![]() .
.
Вычислим производные:
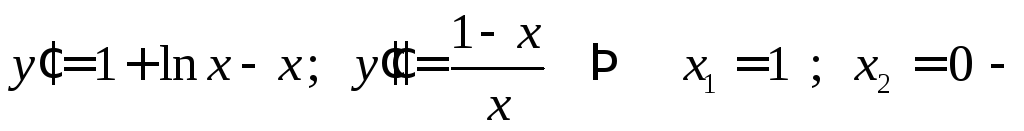 не принадлежит области определения
функции. Построим таблицу
не принадлежит области определения
функции. Построим таблицу
-
х

1
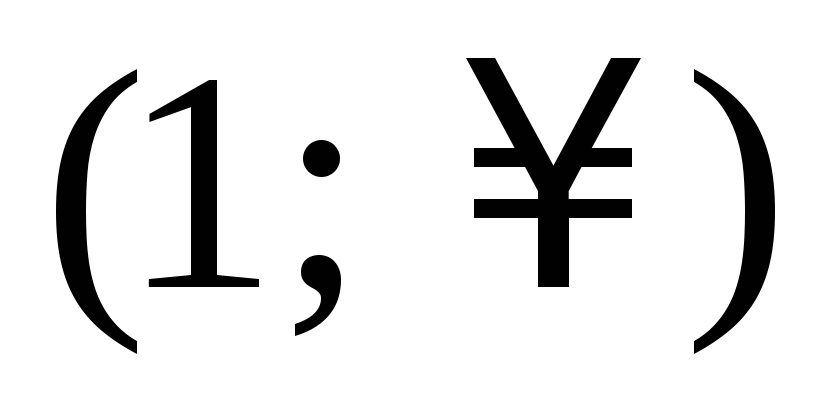
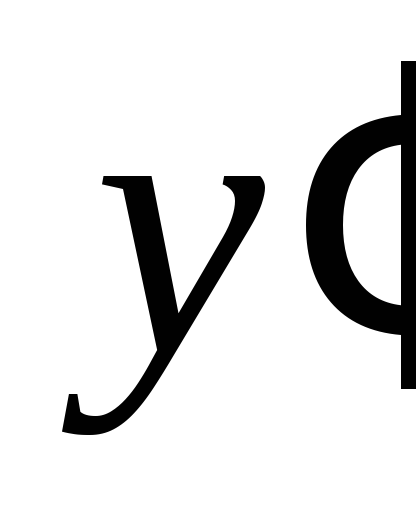
+
0
у
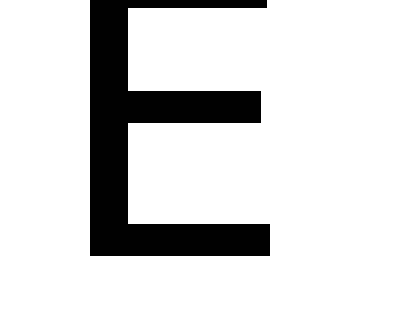
перегиб

Здесь на интервале
![]() функция
функция![]() вогнута, на интервале
вогнута, на интервале![]() функция
функция![]() выпукла,х0
= 1
точка перегиба.
выпукла,х0
= 1
точка перегиба.
