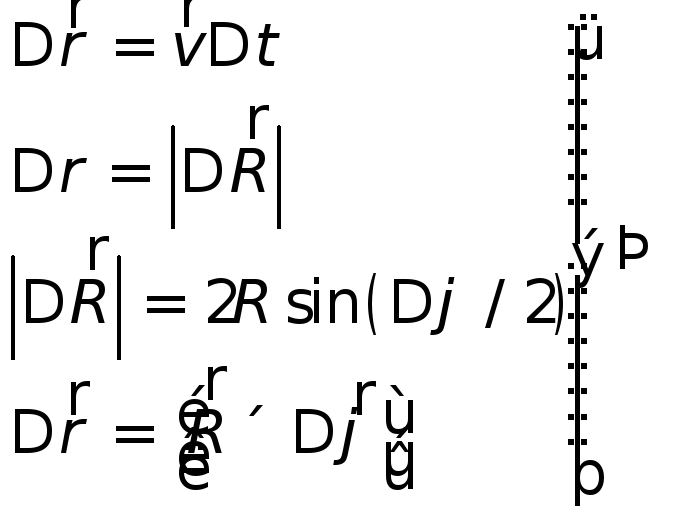1. 2. 3. Угловое ускорение.

Для характеристики быстроты изменения вектора угловой скорости при неравномерном вращательном движении твердого тела вокруг неподвижной оси (или точки) вводится понятие вектора углового ускорения.

Угловым ускорением называется вектор равный производной по времени от угловой скорости или второй производной от угла поворота:

(1.23)

Единица измерения углового ускорения - 1рад/с^2.

При вращении тела вокруг неподвижной оси изменения вектора обусловлены изменениями его численного значения.

Вектор направлен вдоль оси вращения, в ту же сторону что и векторпри(при равноускоренном движении) и при – в противоположную сторону (при равнозамедленном движении).

1. 3. Связь линейных и угловых кинематических величин.

Рассмотрим произвольную точку М твердого тела, вращающегося вокруг неподвижной оси OZ с угловой скоростью , которая описывает окружность радиуса R с центром в точке О. (Рис. 1.10).

Вектор линейной скорости (и перемещения ) точки M лежит в плоскости перпендикулярной оси вращения OZ и перпендикулярен вектору вектору угловой скорости (и углового перемещения ) и радиус-

	вектору . Тогда
Рисунок 1.10.

Следовательно,

(1.24)

Т.к. , то в скалярной форме:

(1.25)

Полученное выражение (1.24) носит название формулы Эйлера. Для ускорения получаем:

Учтем, что

и ,

и окончательно получим:

(1.26)

Первый член в правой части полученного выражения представляет собой рассмотренное ранее тангенциальное ускорение:

(1.27)

Второй член в правой части, учитывая (1.24), преобразуем к виду:

,

(1.28)

т.е. он представляет собой нормальное ускорение.

Пример .

Диск (см. рис.1.10) вращается вокруг вертикальной оси по закону . Найти угловое, нормальное, тангенциальное и полное ускорение точки диска, расположенной на расстоянииR от оси вращения, а также угол между вектором скорости и полного ускорения.

Решение: Имеем по определениям угловой скорости и углового ускорения

По формулам (1.27) и (1.28) находим

,

По формуле (1.18) находим

Угол равен арктангенсу отношения нормального и тангенциального отношения (с точностью до )

1. 4. Преобразование координат, скоростей и ускорений при переходе из одной системы отсчета в другую.

Пусть движение точки в системе отсчетазадано законом. При этом система отсчетасовершает относительно неподвижного наблюдателя сложное движение. Ставится задача о связи кинематических характеристиках движения этой точки в системах отсчетаи, которая неподвижна относительно наблюдателя. Представим это сложное движение системы как сумму поступательного движения системыотносительнои вращения системыотносительнос угловой скоростью(см. рис.1.11).

Рисунок 1.11.

Тогда имеем уравнение

(1.29)

где - радиус-вектор точкис системе,- радиус-вектор начала отсчета системыв,=- радиус-вектор точкис системе(или, т.к. в системахи- радиус-векторы точки[исоответственно] совпадают).

Найдем связь (преобразование) скоростей и ускорений точки в этих системах. Для установления преобразования скоростей дифференцируем (1.29). Имеем:

(1.30)

где -скорость начала координат системы отсчета в системе илипереносная скорость, -скорость точки в системеотсчета или относительная скорость (для неподвижного наблюдателя).

Аналогично для ускорений получаем

(1.31)

где -ускорение начала координат системы отсчета в системе илипереносное ускорение, -ускорение точки С в системе отсчета или относительное ускорение (для неподвижного наблюдателя).

Найдем и . Для этого несколько упростим задачу: будем

	считать, что система отсчета вращается в неподвижной системе отсчета(см. рис. 1.12) вокруг совпадающих осейи. Отметим, что согласно постулатам (аксиомам) классической физики расстояние между точками и временные интервалы между событиями в
Рисунок 1.12.

различных системах отсчета одинаковы.

Следовательно, изменение радиус-векторов точки в указанных системах отсчета. Но, изменение вектораесть только произведение скороститочкив системе отсчетана промежуток времени, а изменение вектораесть результат перемещенияточкисистеме отсчетаи поворота векторана угол, т. е.

(1.32)

Следовательно, скорости точки в этих системах отсчета связаны соотношением

(1.33)

Отметим, что в этом случае - есть относительная, апереносная скорости.

Найдем изменение скорости точкив системе отсчетаза промежуток времени:

(1.34)

Тогда для ускорений получаем

(1.35)

Заметим, что векторное произведение остается неизменным и по величине и по направлению для всех векторов, начала которых лежат на оси вращения. Удобно ввести вектор, направление которого перпендикулярно оси вращения. Тогда=и.

Следовательно,

Поэтому выражение (1.35) примет вид

,

(1.36)

а выражение (1.31) запишем так

,

(1.37)

Раскроем смысл входящих сюда величин. - ускорение тела относительно неподвижного наблюдателя, с которым связана система отсчета,- ускорение тела в системе отсчета,- ускорение начала координат системы отсчета, движущейся поступательно относительно,- так называемоецентростремительное ускорение и, наконец, -кориолисово или поворотное ускорение.

Итак, кинематические величины тела в вышеупомянутых системах отсчета связаны следующим образом

Система отсчета	Радиус-вектор	скорость	ускорение
	=