Центр дерева

Центр графа може складатися з однієї вершини (як, наприклад, в графі ), а може включати всі його вершини (повний граф). Для дерева, як ми побачимо, є набагато вужчий діапазон можливостей.

Теорема 3. Центр дерева складається з однієї вершини або з двох суміжних вершин.

Доведення.

Припустимо, що в деякому дереві є дві несуміжні центральні вершини і. На шляху, що сполучає ці вершини, знайдемо проміжну вершину з максимальним ексцентриситетом, і хай і– вершини, сусідні з на цьому шляху (див. рис. 4.1). Хай – вершина, найбільш віддалена від в дереві, тобто . Шлях, що сполучає з , не може проходити через обидві вершини і. Припустимо, він не проходить через. Тоді єдина шлях зв проходит через і . Звідси витікає, що , а це протирічить вибору вершини , якщо , або тому, що – центральна вершина, якщо .

Отже, будь-які дві центральні вершини суміжні, а оскільки в дереві не може бути три попарно суміжних вершин, то в нім не більше двох центральних вершин.

Мал. 4.1. Кореневі дерева

Часто в дереві особливо виділяється одна вершина, що грає роль свого роду "початку відліку". Дерево з виділеною вершиною називають кореневим деревом, а саму цю вершину – коренем. З дерева з вершинами можна, таким чином, утворити різних кореневих дерев.

При графічному зображенні кореневого дерева зазвичай дотримуються якого-небудь стандарту. Один з найбільш поширених полягає в наступному. Візьмемо на площині сімейство паралельних прямих з рівними відстанями між сусідніми прямими. Змалюємо корінь точкою на одній з цих прямих, суміжні з коренем вершини – точками на сусідній прямій, вершини, що знаходяться на відстані 2 від кореня, – на наступній, і так далі. Ребра зобразимо відрізками прямих. Ясно, що вершини на кожній прямій можна розмістити так, щоб ребра не перетиналися. Приклад намальованого таким чином кореневого дерева показаний на рис. 4.2 (корінь обведений кружком). Частіше, втім, дерево малюють коренем вгору, а не вниз.

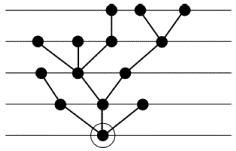
Рис. 4.2.

Інколи буває корисно ребра кореневого дерева орієнтувати так, щоб в кожну вершину вів орієнтований шлях з кореня (для дерева на рис. 3.2 це означає, що кожне ребро орієнтується від низу до верху). Таке орієнтоване кореневе дерево називатимемо витікаючим деревом. У витікаючому дереві кожна вершина, окрім кореня, є кінцем єдиного ребра. Якщо у витікаючому дереві є ребро , то вершину називають батьком вершини , а вершину – сином вершини . Природний і для багатьох цілей зручний спосіб завдання кореневого дерева полягає у вказанні для кожної вершини її батька. При цьому інколи вважають, що корінь доводиться батьком сам собі – це рівносильно додаванню петлі при корені.

Якщо у витікаючому дереві є орієнтований шлях з вершини у вершину , то говорять, що – предок , а – нащадок . Зокрема, кожна вершина є предком і нащадком самій себе. Множина всіх предків вершини породжує орієнтований шлях з кореня в . Множина всіх нащадків вершини породжує витікаюче дерево з коренем в , воно називається гілкою дерева у вершині .

Висотою кореневого дерева називається ексцентриситет його кореня. Якщо ми хочемо перетворити деяке дерево на кореневе і притому мінімальної висоти, то як корінь слід узяти центральну вершину.