
Каркаси
Хай
![]() –звичайний
граф. Його каркасом називається остовный
підграф, в якому немає циклів, а області
зв'язності збігаються з областями
зв'язності графа
–звичайний
граф. Його каркасом називається остовный
підграф, в якому немає циклів, а області
зв'язності збігаються з областями
зв'язності графа ![]() .
Таким чином, каркас зв'язного графу –
дерево, а в загальному випадку – ліс.
.
Таким чином, каркас зв'язного графу –
дерево, а в загальному випадку – ліс.
У
будь-якого графа є хоч би один каркас.
Дійсно, якщо в ![]() немає циклів, то він сам є власним
каркасом. Якщо ж цикли є, то можна видалити
з графа будь-яке ребро, що належить
якому-небудь циклу. Таке ребро не є
перешийком, тому при його видаленні
області зв'язності не зміняться.
Продовжуючи діяти таким чином, після
видалення деякої кількості ребер
отримаємо остовний підграф, в якому
циклів вже немає, а області зв'язності
– ті ж, що у вихідного графа, тобто цей
підграф і буде каркасом. Можна навіть
точно сказати, скільки ребер необхідно
видалити для здобуття каркасу. Якщо в
графі
немає циклів, то він сам є власним
каркасом. Якщо ж цикли є, то можна видалити
з графа будь-яке ребро, що належить
якому-небудь циклу. Таке ребро не є
перешийком, тому при його видаленні
області зв'язності не зміняться.
Продовжуючи діяти таким чином, після
видалення деякої кількості ребер
отримаємо остовний підграф, в якому
циклів вже немає, а області зв'язності
– ті ж, що у вихідного графа, тобто цей
підграф і буде каркасом. Можна навіть
точно сказати, скільки ребер необхідно
видалити для здобуття каркасу. Якщо в
графі ![]() вершин,
вершин, ![]() ребер і
ребер і ![]() компонент зв'язності, то в каркасі буде
теж
компонент зв'язності, то в каркасі буде
теж ![]() вершин і
вершин і ![]() компонент зв'язності. Але в будь-якому
лісі з
компонент зв'язності. Але в будь-якому
лісі з ![]() вершинами і
вершинами і ![]() компонентами зв'язності є рівно
компонентами зв'язності є рівно ![]() ребер. Значить, видалено буде
ребер. Значить, видалено буде ![]() ребер. Це число називається цикломатичним
числом графа і позначається через
ребер. Це число називається цикломатичним
числом графа і позначається через ![]() .
.
Якщо
в графі є цикли, то у нього більше одного
каркасу. Визначити точне число каркасів
зв'язного графа дозволяє так звана
матрична теорема Кірхгофа. Приведемо
її без доведення. Для графа ![]() визначимо матрицю
визначимо матрицю ![]() – квадратну матрицю порядку
– квадратну матрицю порядку ![]() з елементами
з елементами

Інакше
кажучи, ![]() виходить з матриці суміжності, якщо
замінити всі 1 на -1, а замість нулів на
головній діагоналі поставити ступені
вершин. Відмітимо, що матриця
виходить з матриці суміжності, якщо
замінити всі 1 на -1, а замість нулів на
головній діагоналі поставити ступені
вершин. Відмітимо, що матриця ![]() – вироджена, оскільки сума елементів
кожного рядка рівна 0, тобто стовпці
лінійно залежні.
– вироджена, оскільки сума елементів
кожного рядка рівна 0, тобто стовпці
лінійно залежні.
Теорема
4 (матрична теорема Кірхгофа). Якщо ![]() – зв'язний граф з не менше, ніж двома
вершинами, то алгебраїчні доповнення
всіх елементів матриці
– зв'язний граф з не менше, ніж двома
вершинами, то алгебраїчні доповнення
всіх елементів матриці ![]() рівні між собою і дорівнюють числу
каркасів графа
рівні між собою і дорівнюють числу
каркасів графа ![]() .
.
Дводольні графи
Граф
називається дводольним,
якщо множину його вершин можна так
розбити на дві підмножини, аби кінці
кожного ребра належали різним підмножинам.
Ці підмножини називаються долями.
Таким чином, кожна з доль породжує
порожній підграф. Прикладом дводольного
графа є простий ланцюг ![]() при будь-якому
при будь-якому ![]() :
одна доля породжується вершинами з
парними номерами, інша – з непарними.
Граф
:
одна доля породжується вершинами з
парними номерами, інша – з непарними.
Граф ![]() – приклад графа, що не є дводольним: при
будь-якому розбитті множини його вершин
на дві підмножини в одній з цих підмножин
виявляться дві суміжні вершини.
– приклад графа, що не є дводольним: при
будь-якому розбитті множини його вершин
на дві підмножини в одній з цих підмножин
виявляться дві суміжні вершини.
Прикладне
значення поняття дводольного графа
пов'язане з тим, що за допомогою таких
графів моделюються відношення між
об'єктами двох типів, а такі стосунки
часто зустрічаються на практиці
(наприклад, відношення "продукт ![]() використовується у виробництві виробу
використовується у виробництві виробу
![]() "
між вихідними продуктами і готовими
виробами, або "працівник
"
між вихідними продуктами і готовими
виробами, або "працівник ![]() володіє професією
володіє професією ![]() "
між працівниками і професіями). У
математиці такі стосунки теж нерідкі,
один з найбільш поширених їх видів –
відношення інцидентності. Хай
"
між працівниками і професіями). У
математиці такі стосунки теж нерідкі,
один з найбільш поширених їх видів –
відношення інцидентності. Хай ![]() – множина, а
– множина, а ![]() – сімейство його підмножин. Елемент
– сімейство його підмножин. Елемент ![]() і множина
і множина ![]() інцидентні
один одному, якщо
інцидентні
один одному, якщо ![]() .
Відношення інцидентності можна описати
за допомогою дводольного графа, в якому
.
Відношення інцидентності можна описати
за допомогою дводольного графа, в якому
![]() ,
,![]() .
На рис. 4.3 показаний граф відношення
інцидентності для
.
На рис. 4.3 показаний граф відношення
інцидентності для![]() ,
,
![]() ,
де
,
де![]() ,
,![]() ,
,![]() ,
,![]() .
.
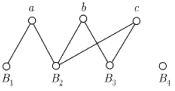
Рис. 3.3.
Взагалі
кажучи, розбиття множини вершин
дводольного графу на долі можна здійснити
не єдиним способом. Так, в графі з тільки
що наведеного прикладу можна взяти за
долі множину
![]() і
і![]() .
В той же час в самому визначенні цього
графу вже закладено "природне"
розбиття на долі
.
В той же час в самому визначенні цього
графу вже закладено "природне"
розбиття на долі![]() і
і ![]() .
Дводольні графи, що виникають в додатках,
часто бувають задані саме так – з
множиною вершин, що спочатку складається
з двох частин, і з множиною ребер, кожне
з яких сполучає вершини з різних частин.
.
Дводольні графи, що виникають в додатках,
часто бувають задані саме так – з
множиною вершин, що спочатку складається
з двох частин, і з множиною ребер, кожне
з яких сполучає вершини з різних частин.
Якщо
розбиття на долі не задане, то може
виникнути питання, чи існує воно взагалі,
тобто чи є даний граф дводольним? Якщо
в графі ![]() вершин, то є
вершин, то є ![]() розбиття множини вершин на дві підмножини
і безпосередня перевірка всього цього
розбиття буде дуже трудомісткою справою.
Наступна теорема дає критерій дводольності,
а з її доведення можна отримати і
ефективний алгоритм перевірки
дводольності. Детально такий алгоритм
буде описаний в наступному занятті.
розбиття множини вершин на дві підмножини
і безпосередня перевірка всього цього
розбиття буде дуже трудомісткою справою.
Наступна теорема дає критерій дводольності,
а з її доведення можна отримати і
ефективний алгоритм перевірки
дводольності. Детально такий алгоритм
буде описаний в наступному занятті.
Теорема 5. Наступні твердження для графа рівносильні:
(1)
 -
дводольний граф;
-
дводольний граф;(2) у
 немає циклів непарної довжини;
немає циклів непарної довжини;(3) у
 немає простих циклів непарної довжини.
немає простих циклів непарної довжини.
Доведення.
Доведемо,
що з (1) слідує (2). Хай
![]() – дводольний граф, в якому вибрано деяке
розбиття на долі,
– дводольний граф, в якому вибрано деяке
розбиття на долі, ![]() – цикл довжини
– цикл довжини ![]() в графі
в графі
![]() .
При будь-якому
.
При будь-якому ![]() вершини
вершини ![]() і
і ![]() суміжні і, отже, належать різним долям.
Таким чином, одна доля складається зі
всіх вершин з непарними індексами, тобто
суміжні і, отже, належать різним долям.
Таким чином, одна доля складається зі
всіх вершин з непарними індексами, тобто
![]() ,
інша – зі всіх вершин з парними індексами.
Але вершини
,
інша – зі всіх вершин з парними індексами.
Але вершини
![]() і
і![]() теж суміжні і повинні належати різним
долям. Отже,
теж суміжні і повинні належати різним
долям. Отже,![]() – парне число.
– парне число.
Вочевидь,
що з (2) слідує (3); залишається довести,
що з (3) слідує (1). Розглянемо граф ![]() ,
в якому немає простих циклів непарної
довжини. Ясно, що граф, в якому кожна
компонента зв'язності – дводольний
граф, сам дводольний. Тому можна вважати,
що граф
,
в якому немає простих циклів непарної
довжини. Ясно, що граф, в якому кожна
компонента зв'язності – дводольний
граф, сам дводольний. Тому можна вважати,
що граф ![]() зв'язний. Зафіксуємо в ньому деяку
вершину
зв'язний. Зафіксуємо в ньому деяку
вершину ![]() і доведемо, що для будь-яких двох суміжних
між собою вершин
і доведемо, що для будь-яких двох суміжних
між собою вершин ![]() і
і ![]() має місце рівність
має місце рівність ![]() .
Дійсно, допустимо спочатку, що
.
Дійсно, допустимо спочатку, що ![]() .
Хай
.
Хай ![]() – найкоротший шлях з
– найкоротший шлях з ![]() в
в ![]() – найкоротший шлях з
– найкоротший шлях з ![]() в
в ![]() .
Ці шялхи починаються в одній вершині:
.
Ці шялхи починаються в одній вершині:
![]() ,
а закінчуються в різних:
,
а закінчуються в різних:![]() ,
,
![]() .
Тому знайдеться таке
.
Тому знайдеться таке ![]() ,
що
,
що ![]() і
і ![]() при всіх
при всіх ![]() .
Але тоді послідовність
.
Але тоді послідовність ![]() є простим циклом довжини
є простим циклом довжини ![]() .
Отже,
.
Отже, ![]() .
Вважатимемо, що
.
Вважатимемо, що ![]() .
Якщо
.
Якщо ![]() – найкоротший шлях з
– найкоротший шлях з ![]() в
в ![]() ,
то, вочевидь, що
,
то, вочевидь, що ![]() – найкоротший шлях з
– найкоротший шлях з ![]() в
в ![]() ,
отже
,
отже ![]() .
Отже, відстані від двох суміжних вершин
до вершини
.
Отже, відстані від двох суміжних вершин
до вершини ![]() розрізняються рівно на одиницю. Тому,
якщо позначити через
розрізняються рівно на одиницю. Тому,
якщо позначити через ![]() множину всіх вершин графу, відстань від
яких до вершини
множину всіх вершин графу, відстань від
яких до вершини ![]() парна, а через
парна, а через ![]() множину всіх вершин з непарними відстанями
до
множину всіх вершин з непарними відстанями
до ![]() ,
то для кожного ребра графу один з його
кінців належить множині
,
то для кожного ребра графу один з його
кінців належить множині ![]() ,
інший – множині
,
інший – множині ![]() .
Отже, граф
.
Отже, граф ![]() – дводольний.
– дводольний.
Хай
![]() – цикл в графі
– цикл в графі ![]() .
Множина вершин циклу
.
Множина вершин циклу ![]() породжує в
породжує в ![]() підграф, який містить всі ребра цього
циклу, але може містити і ребра, що йому
не належать. Такі ребра називають хордами
циклу
підграф, який містить всі ребра цього
циклу, але може містити і ребра, що йому
не належать. Такі ребра називають хордами
циклу ![]() .
Простий цикл, що не має хорд, – це
породжений простий цикл. У графові,
зображеному на рис. 4.4, хордами циклу
.
Простий цикл, що не має хорд, – це
породжений простий цикл. У графові,
зображеному на рис. 4.4, хордами циклу ![]() є ребра,
є ребра,
![]() ,
,![]() і
і![]() ,
а цикл
,
а цикл![]() – породжений простий цикл. Відмітимо,
що будь-який цикл довжини 3 є породженим
простим циклом.
– породжений простий цикл. Відмітимо,
що будь-який цикл довжини 3 є породженим
простим циклом.

Рис. 4.4.
Хай
![]() – простий цикл довжини
– простий цикл довжини ![]() в деякому графові,
в деякому графові, ![]() – хорда цього циклу. Ребро
– хорда цього циклу. Ребро ![]() разом з ребрами циклу
разом з ребрами циклу ![]() утворює два цикли меншої довжини,
утворює два цикли меншої довжини,
![]() і
і![]() (див. рис. 4.5), сума довжин яких рівна
(див. рис. 4.5), сума довжин яких рівна![]() .
.

Рис. 4.5.
Значить,
якщо ![]() – цикл непарної довжини, то один з циклів
– цикл непарної довжини, то один з циклів
![]() і
і![]() теж має непарну довжину. Звідси витікає,
що в графові, в якому є цикл непарної
довжини, є і породжений простий цикл
непарної довжини. Тому критерій
дводольності справедливий і в наступному
формулюванні.
теж має непарну довжину. Звідси витікає,
що в графові, в якому є цикл непарної
довжини, є і породжений простий цикл
непарної довжини. Тому критерій
дводольності справедливий і в наступному
формулюванні.
Наслідок. Граф є дводольним тоді і лише тоді, коли в ньому немає породжених простих циклів непарної довжини.
