Операції над графами

Для отримання нових графів можна використовувати різноманітні операції над графами. Тут ми розглянемо два види операцій – локальні, при яких замінюються, видаляються або додаються окремі елементи графа, і алгебра, коли новий граф будується за певними правилами з декількох наявних.

Локальні операції

Проста операція – видалення ребра. При видаленні ребра зберігаються всі вершини графа і всі його ребра, окрім того, що видаляється. Зворотна операція – додавання ребра.

При видаленні вершини разом з вершиною видаляються і всі інцидентні їй ребра. Граф, що отримується з графа видаленням вершини ,позначають . При додаванні вершини до графа додається нова ізольована вершина. За допомогою операцій додавання вершин і ребер можна ні "з чого", тобто з графа побудувати будь-який граф.

Операція стягування ребра визначається таким чином. Вершини івидаляються з графа, до нього додається нова вершина ,і вона з'єднується ребром з кожною вершиною, з якою була суміжна хоч би одна з вершин .

Операція підрозбиття ребра діє таким чином. З графа видаляється це ребро, до нього додається нова вершина і два нові ребра і. На рис. 1.10 зображені початковий граф граф ,отриманий з нього стягуванням ребра та ,отриманий підрозбиттям того ж ребра. У обох випадках знов додана вершина позначена цифрою 7.

Рис. 1.10.

Підграфи

Граф називається підграфом графа ,якщо , . Всякий підграф може бути отриманий з графа видаленням деяких вершин і ребер. На рис. 1.11 зображені граф і його підграфи ,,,.

Рис. 1.11.

Підграф графа називається остовним, якщо . Остовний підграф може бути отриманий з графа видаленням деяких ребер, вершини ж залишаються в недоторканності. На рис. 1.11 –остовний підграф графа ,а ,іне є остовними підграфами.

Інший важливий різновид підграфів – породжені підграфи. Хай задано граф і в ньому вибрана множина вершин . Розглянемо підграф ,де складається зі всіх тих ребер графа ,у яких обидва кінці належать . Говорять, що цей підграф породжений множиною вершин . Він позначається через . Породжений підграф може бути отриманий з графа видаленням "зайвих" вершин, тобто вершин, що не належать .

Можна визначити також підграф, породжений множиною ребер . Це підграф ,де складається зі всіх вершин, інцидентних ребрам з .

На рис. 1.11 –підграф графа ,породжений множиною вершин , тобто ,він же породжується множиною ребер ; підграф не породжується множиною вершин, але породжується множиною ребер ; підграф не є ні остовним, ні породженим в якому-небудь сенсі.

Алгебраїчні операції

Оскільки граф складається з двох множин (вершини і ребра), то різні операції над множинами природним чином породжують відповідні операції над графами. Наприклад, об'єднання двох графів івизначається як граф ,у якого ,,а перетин – як граф ,у якого ,. Обидві операції ілюструє рис. 1.12.

Рис. 1.12.

Доповненням (додатковим графом) до графа називається граф ,у якого множина вершин та ж, що у ,а множина ребер є доповненням множини до множини всіх невпорядкованих пар вершин. Інакше кажучи, дві різні вершини суміжні в графі тоді і тільки тоді, коли вони несуміжні в графі . Наприклад, . Інший приклад показаний на рис. 1.13. Очевидно, що завжди .

Рис. 1.13.

Під сумою двох абстрактних графів розуміють об'єднання графів з множинами вершин, які не перетинаються. Точніше кажучи, мається на увазі наступне. Спочатку вершинам графів-доданків присвоюються імена (позначки, номери) так, щоб множини вершин не перетиналися, потім отримані графи об'єднуються. Операція додавання асоціативна, тобто для будь-яких трьох графів. Тому можна утворювати суму будь-якого числа графів, не вказуючи порядку дій за допомогою дужок. Якщо додаються екземплярів одного і того ж графа ,то отриманий граф позначається через . Наприклад . На рис. 1.14 зображений граф .

Рис. 1.14.

Рис. 1.15.

З'єднанням двох графів і називається граф, що отримується з їх суми додаванням всіх ребер, що сполучають вершини першого доданку з вершинами другого. Записуватимемо цю операцію як . На рис. 1.15 представлений граф . Легко бачити, що операції додавання і з'єднання графів зв'язані одна з одною наступними простими співвідношеннями:

Введемо ще два типи спеціальних графів, які легко описуються за допомогою операції з'єднання. Перший – повний дводольний граф . У цьому графові множина вершин розбита на дві підмножини (долі), в одному з яких вершин, в іншому ,і дві вершини в ньому суміжні тоді і тільки тоді, якщо вони належать різним підмножинам. Другий – колесо . На рис. 1.16 показані графи і.

Рис. 1.16.

Добуток графів і визначається таким чином. Множиною вершин графа є декартовий добуток множин і ,тобто вершини цього графа – впорядковані пари ,де –вершина першого співмножника, –вершина другого. Вершини івсуміжні тоді і тільки тоді, якщо та суміжна з у графі ,або і суміжна з у графі . За допомогою операції добутку можна виразити деякі важливі графи через прості. Наприклад, добуток двох ланцюгів дає прямокутну решітку (див. рис. 1.17). Якщо один із співмножників перетворити на цикл, додавши одне ребро, то прямокутна решітка перетвориться на циліндрову, а якщо і другий співмножник перетворити на цикл, то вийде тороїдальна решітка.

Рис. 1.17.

Інший приклад – -мірний куб , якийвизначається таким чином. Вершинами його є всі можливі впорядковані двійкові набори довжини . Всього, таким чином, в цьому графові вершин. Вершини і ^y=(y₁^,…y_k⁾ суміжні в ньому тоді і тільки тоді, коли набори тарозрізняються тільки в одній координаті. За допомогою операції добутку граф можна визначити рекурсивно:

На рис. 1.18 показано, як виходить з .

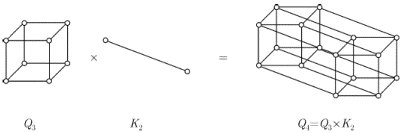
Рис. 1.18.