ТЕОРИЯ ОПТИМИЗАЦИИ И Алгоритмов / Методы_оптимизации

91

10. МЕТОДЫ ОТСЕЧЕНИЙ

Методы отсечений относятся к численным методам решения дискретных задач оптимизации (методам дискретного программирования). Они предназначены для решения целочисленных задач линейного программирования (ЛП). Идея методов отсечения состоит в следующем.

Первоначально решается обычная ("непрерывная") задача ЛП, полученная из исходной задачи отбрасыванием требования целочисленности. Если полученное решение является целочисленным, то оно будет также решением исходной задачи. Если нет, то к ограничениям исходной задачи добавляется новое линейное ограничение, обладающее двумя свойствами:

1)полученное нецелочисленное решение ему не удовлетворяет;

2)все целочисленные точки допустимого множества исходной задачи ему удовлетворяют.

Такое ограничение называется правильным отсечением. Затем решается расширенная непрерывная задача ЛП, т.е.

непрерывная задача с добавленным ограничением. Если полученное решение не является целочисленным, добавляется новое правильное отсечение и т.д. Процесс повторяется до тех пор, пока решение очередной расширенной непрерывной задачи ЛП не окажется целочисленным. Таким образом, решение целочисленной задачи ЛП сводится к решению некоторой последовательности обычных задач ЛП.

Геометрически добавление каждого такого линейного ограничения означает проведение гиперплоскости, отсекающей от многогранника допустимых решений очередной непрерывной задачи ЛП оптимальную точку с нецелочисленными координатами, но не затрагивающей ни одной из целочисленных точек этого многогранника. Поэтому методы, опирающиеся на эту идею, получили название методов отсечений.

Обозначим через Lk и x(k ) , k=0,1,..., соответственно k-ю

расширенную непрерывную задачу ЛП и ее решение. Отметим, что L0 представляет собой исходную задачу без учета требова-

92

ний целочисленности. Задача Lk+1 получается в результате добавления к ограничениям задачи Lk (k+1)-го правильного отсечения.

Алгоритм решения целочисленной задачи ЛП методом отсечений заключается в следующем.

1. Решается задача ЛП L0.

Если задача L0 не имеет решения, то исходная задача не имеет целочисленного решения и вычисления завершаются.

2. Находится решение x(0) .

Если решение x(0) является целочисленным, то полагается x = x(0) , f = f (x(0) ) и вычисления завершаются.

Если решение x(0) не является целочисленным, то полагается k = 1 и осуществляется переход к п. 3.

3. Определяется k-е правильное отсечение, составляется

задача Lk.

4. Решается задача ЛП Lk.

Если задача Lk не имеет решения, то исходная задача не имеет целочисленного решения и вычисления завершаются.

5. Находится решение x(k ) .

Если решение x(k ) является целочисленным, то полагается

x = x(k ) ,

f = f (x(k ) ) и вычисления завершаются.

Если решение x(k ) не является целочисленным, то полагается k = k +1 и осуществляется переход к п. 3.

Конкретные способы построения правильных отсечений приводят к конкретным вычислительным алгоритмам.

На практическом занятии рассматривается первый (дробный) алгоритм Гомори, предназначенный для решения полностью целочисленных задач ЛП. Рассмотрим полностью целочисленную задачу ЛП:

n

f (x) = ∑ c j x j → max ,

j=1

93

n

∑ aij x j ≤ bi , i = 1, m ,

j=1

x j ≥ 0 ,	j =	1, n		,
x j − целые,	j =				.
			1, n

Отметим, что для применения первого алгоритма Гомори все коэффициенты и правые части ограничений исходной задачи должны быть приведены к целочисленному виду.

Первоначально решается задача L0. Пусть решение x(0) этой задачи не является целочисленным. Согласно общему алгоритму, следует определить дополнительное ограничение (1-е правильное отсечение). Пусть последняя симплекс-таблица задачи L0 имеет следующий вид:

Базис

Своб.

x′

...

x′

x′′

...

x′′

член

1

m

1

n

x′

1

...

0

...

b1

a11

a1n

1

"

"

"

...

"

"

...

"

x′

0

...

1

...

bm

am1

amn

m

f

0

...

0

...

n

b

0

c

1

c

Здесь через xi′ ,

i =

, обозначены базисные переменные,

1, m

а через

x′j′ , j =

,

− свободные переменные.

Такая система

1, n

обозначений выбрана из соображений удобства.

Строки симплекс-таблицы, которым соответствуют нецелые значения базисных переменных, т.е. нецелые bi , называют

производящими. Каждая производящая строка задает правильное отсечение, которое определяется следующим образом: i-я производящая строка записывается в виде

	n
(1+ 0)x′	+ ∑ ([aij ] +{aij })x′′j	= [	bi	] + {	bi	},
i	j =1

94

где [а] и {a} − соответственно целая и дробная части действительного числа а, a = [a] + {a}.

Эта производящая строка задает правильное отсечение следующего вида:

n

− ∑{aij }x′′j + u1 = −{bi } ,

j =1

где u1 − неотрицательная дополнительная переменная, которая

(по определению) должна принимать целые значения.

Выбор производящей строки для построения правильного отсечения осуществляется с помощью эмпирических правил. Первое из них предписывает выбирать производящую строку, которой соответствует

	max{	bi	},
	i
второе − строку, которой соответствует
				n
max di ≡ {bi }				∑	{aij } .
i				j =1

Если с помощью указанных правил не удается выбрать производящую строку для построения правильного отсечения, производящая строка выбирается произвольно.

В результате добавления к ограничениям задачи L0 дополнительного ограничения (1-го правильного отсечения) получаем

	задачу L1, т.е.
			L0 ,
			n
	L1			+ u1	= −{bi },
		− ∑{aij }x′′j
			j =1
			u ≥ 0.
			1

Наиболее удобным методом решения задачи L1 в указанной постановке является двойственный симплекс-метод. При этом дополнительная переменная u1 вводится в базис, а дополни-

тельное ограничение добавляется к итоговой симплекс-таблице

задачи L0.

Пример. Решить методом отсечений следующую цело-

95

численную задачу ЛП:

f(x) = 7x1 + 9x2 → max ,

−x1 + 3x2 ≤ 6 ,

7x1 + x2 ≤ 35 , x1 ≥ 0 , x2 ≥ 0 , x1, x2 − целые.

Решение.

Нулевой этап

Записываем задачу L0 (исходная задача без учета требования целочисленности):

f(x) = 7x1 + 9x2 → max ,

−x1 + 3x2 ≤ 6,

7x1 + x2 ≤ 35 , x1 ≥ 0 , x2 ≥ 0 .

Решаем задачу L0 симплекс-методом. Для этого преобразуем задачу к канонической форме, вводя дополнительные переменные x3 и x4:

f(x) = 7x1 + 9x2 → max ,

−x1 + 3x2 + х3 = 6 ,

7x1 + x2 + х4 = 35 , x j ≥ 0 , j = 1,4 .

В качестве базисных выберем переменные x3 и x4 . Таким образом, начальный базис Б0 = {x3 , x4}. В результате приходим к

табл. 10.1.

Из табл. 10.1 следует, что начальное допустимое базисное решение ДБР0 = (x3=6, x4=35). ДБР 0 не является оптимальным,

поскольку в	строке целевой функции есть отрицательные коэф-
фициенты	fx1	= −7, fx2 = −9 . Задача разрешима, поскольку в
столбцах x1	и	x2 есть положительные коэффициенты. Находим
Б1 :

				96
				↓		Таблица 10.1
	Базис	Своб.	x1	x2	x3			x
		член						4
→	x3	6	−1	3	1			0		6/3=2
	x4	35	7	1	0			1		35/1=35
	f	0	−7	−9	0			0

fx2

< 0,

fx2

< fx1 → x2

вводим в базис,

min{6 3 = 2, 35 1 = 35}= 2 →

x3

`выводим из базиса.

Таким

образом,

Б1 = {x2 , x4}. В

результате

приходим

к

табл. 10.2.

Таблица 10.2

↓

Базис

Своб.

x1

x2

x3

x4

член

x2

2

−

1

1

1

0

3

3

33 3

→

x4

33

22

0

−

1

1

=

9

3

22

3

2

f

18

−10

0

3

0

Из табл. 10.2

следует, что ДБР1 = (х2 = 2, х4 = 33) .

ДБР1

не является оптимальным

( fx = −10 < 0) ,

задача разрешима (в

1

столбце x1 есть положительный коэффициент). Находим Б2 :

fx

< 0

→ x1 вводим в базис,

1

x4

выводим из базиса.

Таким образом,

Б2 = {x1, x2 }. В результате

приходим

к

табл. 10.3.

97

														Таблица 10.3
	Базис		Своб.				x1	x2		x3								x4
			член
	x1		4		1		1	0	−		1							3
																	22
			2						22
	x2			1			0	1		7								1
			3 2						22								22
	f		63				0	0				6								4
									211							111
															1								1
	Из	табл. 10.3					следует,	что ДБР2	= x1 = 4							, x2	= 3							,
															2								2
ДБР2 является оптимальным решением.
																	1						1
														(0)
	Таким образом, задача L0 имеет решение х														= 4					, 3				,
																	2						2
при этом		f (х(0) ) = 63.

Поскольку x(0) не является целочисленным, то выполняем 1-й этап.

Первый этап Определяем первое правильное отсечение. Производящи-

ми являются 1-я и 2-я строки итоговой симплекс-таблицы задачи

L0.

Поскольку {b1} = 12 и {b2 } = 12 , то первое правило не по-

зволяет выбрать производящую строку для построения отсечения. Используем второе правило выбора производящей строки. Вычисляем d1 и d2 :

		=	1		21	+	3		=	11		=	1	7		+	1		=	11
	d1										, d2										.
			2		22		22			24			2		22		22			8

Поскольку d1 < d2, то для построения 1-го правильного отсечения выбираем 2-ю строку итоговой симплекс-таблицы задачи L0. 2-й строке соответствует равенство

										98
								7							1						1
(1 + 0)x2	+ 0				+				x3 + 0 +							x4				= 3 +		.
								22							22						2
Следовательно, 1-е правильное отсечение имеет вид
	−		7		x −				1		x			+ u = −			1	.
									22
	22					3						4		1		2
Составляем задачу L1:
											L0 ,
L1					7			x3			1			x4 + u1 = −					1	,
	−								−
				22						22
																2
										u1 ≥ 0.

			Решаем задачу L1 двойственным симплекс-методом.
			В качестве базисных выберем переменные x1, x2 , u1. Та-
ким образом,							Б0 = {x1, x2 , u1}. В результате приходим к табл. 10.4.
																						↓							Таблица 10.4
			Базис				Своб.								x1			x2			x3							x4						u1
							член
			x1				4			1					1			0		−		1						3						0
										2																	22
																				22
			x2				3			1					0			1			7							1						0
										2										22							22
→		u1					−			1					0			0		−			7				−		1					1
										2
																				22							22
			f				63								0			0					6						4					0
																				211							111
																				8							30
			Из табл. 10.4 следует, что начальное базисное решение БР0
				1							1					1
= x1			= 4		, x2 = 3								, u1		= −		. БР0		не является допустимым, по-
				2							2
																2

скольку в столбце свободных членов есть отрицательный коэф-

99

фициент bu1 = −1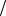2 < 0 . Задача разрешима, поскольку в строке u1

	есть отрицательные коэффициенты. Находим Б1 :
												bu	< 0				→		u1 выводим из базиса,
												1
	28						7							15				1
	min					−						= 8,					−			= 30 = 8			→ x3		вводим в базис.
		11					22							11				22
		Таким образом,															Б1 = {x1, x2 , x3}.						В результате приходим к
	табл. 10.5.																										Таблица 10.5
	Базис					Своб.									x1					x2			x3		x4									u1
						член
	x1								4					1						0			0			1									1
							4 7																		7								− 7
	x2						3							0						1			0		0								1
	x3						1		4					0						0			1			1						− 3				1
									7																7
																																			7
	f						59							0						0			0		1								8
																													4
		Из				табл.							10.5				следует,				что		БР1 =		х1		=	4				, х2			= 3,
																													7
		4
	х3 = 1		. БР1 является допустимым и, следовательно, оптималь-
		7
	ным решением.																																4
																											(1)
		Таким образом,															задача L1				имеет решение x							=				4			, 3 ,
																																	7
	при этом					f (x(1) ) = 59.

Поскольку x(1) не является целочисленным, то выполняем 2-й этап.

Второй этап Определяем второе правильное отсечение. Производящими

являются 1-я и 3-я строки итоговой симплекс-таблицы задачи L1.

100

Поскольку {b1} = 74 и {b3} = 47 , то первое правило не по-

зволяет выбрать производящую строку для построения отсечения. Используем второе правило выбора производящей строки.

	Вычисляем d1 и d2 :
			4		1		6			4			4	1			6			4
	d1	=				+			=		, d2	=				+			=		.
			7		7		7			7			7		7		7			7

Поскольку d1 = d2 , то второе правило не позволяет вы-

брать производящую строку для построения отсечения. Выберем произвольно 1-ю строку итоговой симплекс-таблицы задачи L1. Этой строке соответствует равенство

											1													6							4
	(1 + 0)x1 +			0			+						x4 +							− 1		+					u1			= 4 +		.
											7													7							7
Следовательно, 2-е правильное отсечение имеет вид
			−		1	x					−			6		u + u						= −					4	.
														7													7
				7					4								1				2
Составляем задачу L2:
							1										6		L1,										4
			L2								x4								u1 + u2											,
				−										−											= −
							7										7												7
																	u2			≥ 0.
Решаем задачу L2 двойственным симплекс-методом.
В	качестве базисных														выберем									переменные x1, x2 , x3 ,u2 .
Таким образом, Б0 = {x1 , x2 , x3 , u2 }.																						В результате приходим к
табл. 10.6.
Из табл. 10.6 следует, что начальное базисное решение
		4											4									4
БР0 = x1	= 4		, x2 = 3, x3				=				1				, u2					= −				. БР0 не является допус-
		7											7									7
тимым, поскольку bu2				= − 4 7 < 0 ; задача разрешима, поскольку в
строке u2	есть отрицательные коэффициенты. Находим Б1 :