ТЕОРИЯ ОПТИМИЗАЦИИ И Алгоритмов / Методы_оптимизации

71

~	(k −1)	) + gi′(x	(k −1)	),(x − x	(k −1)	)	≤ 0,	i = 1, r,
gi (x) = gi (x

x R+n.

Затем находится решение x0 задачи ЛП, после чего опре-

деляется точка x(k ) по известным x(k−1) и x0 . Эта точка должна удовлетворять условиям

x(k ) X ,

(8.1)

f (x(k ) ) < f (x(k −1) ).

Существует много способов определения x(k ) . На практическом занятии x(k ) определяется из соотношения

x(k ) = x(k −1) + λ	(x0 − x(k −1) ),	0 ≤ λ	k	≤ 1, k = 1,2,...,
k

где λk − параметр (скаляр), определяющий длину шага из точки x(k−1) в направлении точки x0 .

Очевидно, что при λk = 1 выполняется x(k ) = x0 , при

λk = 0 x(k ) = x(k −1) .

Величина λk выбирается так, чтобы выполнялись условия

(8.1). Процесс выбора шага, удовлетворяющего данным условиям, во многом аналогичен соответствующему процессу в случае градиентного метода с дроблением шага. Выбирается константа 0 < β < 1 (в данном случае α =1). На k-й, k = 1,2,..., итерации

проверяется выполнение условий (8.1) при λk=1, т.е. для x(k) = x0 . Если они не выполняются, то производится дробление шага, т.е. полагается λk = β , и вновь проверяется выполнение условий (8.1). Процесс дробления, т.е. умножения текущего значения λk на β , продолжается до тех пор, пока условия (8.1) не

окажутся выполненными.

Алгоритм решения задачи условной минимизации методом аппроксимирующего программирования заключается в следующем.

1. Задаются β , δ1 , δ 2 ; выбирается x(0) ; полагается k = 1.

≤ δ1,

72

2.Осуществляется линеаризация исходной задачи в окрестности точки x(k −1) . В результате получается задача ЛП.

3.Находится решение x0 задачи ЛП.

4.Полагается λk = 1.

5.Вычисляется x(k ) = x(k −1) + λk (x0 − x(k −1) ) .

6.Проверяются условия выбора x(k ) :

gi (x(k ) ) ≤ 0, i = 1, r; f (x(k ) ) < f (x(k −1) ).

Если они выполняются, то осуществляется переход к п.7. Если условия не выполняются, то полагается λk = λk β и

осуществляется переход к п.5.

7. Проверяются условия окончания решения исходной задачи: f (x(k ) ) − f (x(k −1) )

f (x(k −1) )

x(jk ) − x(jk −1)

≤ δ

2 ,

j =

1, n.

x(jk −1)

Если

они выполняются,

то

полагается

x* x(k ) ,

f * f (x(k ) )

и вычисления завершаются.

Если условия не выполняются, то полагается

k = k +1 и

осуществляется переход к п.2.

Пример. Решить методом аппроксимирующего программирования задачу условной минимизации

f (x) = 4x1 − x22 −12 → min,

	x2	+ x2	≤ 25,
	1	2
10x	− x2	+10x		− x2	≥ 34,
1	1		2	2
	x1 ≥ 0,		x2 ≥ 0
при β = 0,7 , δ1 = 0,1, δ 2	= 0,3 .

73

Решение.

Преобразуем

ограничения

исходной

задачи

к виду

gi (x) ≤ 0 :

g (x) = x2

+ x2

− 25 ≤ 0,

1

1

2

g

2

(x)

= x2 −10x + x2

−10x + 34 ≤

0.

1

1

2

2

Находим

f ′(x) ,

g′(x) ,

g′ (x) :

∂f

∂f

1

2

= 4,

= −2x2

→

f ′(x) = (4,−2x2 );

∂x1

∂x2

∂g1 = 2x ,

∂g1 = 2x

2

→ g′

(x) = (2x

,2x

2

);

∂x1

1

∂x2

1

1

∂g2 = 2x −10,

∂g2 = 2x

2

−10

→

g′

(x) = (2x −10,2x

2

−10).

1

∂x2

2

1

∂x1

Выберем x(0)

= (2, 4) .

Проверяем принадлежность точки x(0) к допустимой об-

ласти X:

g1 (x(0) ) = 22

+ 42 − 25 = −5 < 0,

g2 (x(0) ) = 22 −10 2 + 42 −10 4 + 34 = −6 < 0,

x(0)

>

0,

x(0) > 0.

1

2

Поскольку

ограничения

выполняются,

то

точка

x (0) = (2, 4) является допустимой, т.е. x(0) X .

Первый этап (первая итерация)

Осуществляем линеаризацию исходной задачи в окрестности точки x(0) :

f (x(0) ) = 4 2 − 42 −12 = 8 −16 −12 = −20,

f ′(x(0) ) = (4, − 2 4) = (4, − 8),
~	+ (4,	−8), (x1 − 2,	x2 − 4)	=
f (x) = −20

74

= −20 + 4(x1 − 2) − 8(x2 − 4) = 4x1 − 8x2 + 4;

	g′(x(0) ) = (2 2, 2 4) = (4, 8),
	1
~			8), (x1 − 2, x2 − 4)	=
g1(x) = −5 + (4,
= −5 + 4(x1 − 2) + 8(x2 − 4) = 4x1 + 8x2 − 45;
g′	(x(0) ) =	(2 2 −10, 2 4 −10) = (−6, − 2),
2
~	(x) = −6	+ (−6,	−2), (x1 − 2, x2 − 4)	=
g2
= −6 − 6(x1 − 2) − 2(x2 − 4) = −6x1 − 2x2 +14.
Составляем задачу ЛП:
		~
		f (x) = → min,
		~	(x) ≤ 0;
		g1
		~	(x) ≤ 0;
		g2

	~	x1 ≥ 0,		x2 ≥ 0.
Подставляем		~		~
	f (x), g1 (x), g2 (x) :
	~	= 4x1 − 8x2 + 4 → min ,
	f (x)
		4x1 + 8x2 ≤ 45 ,			(1)
		6x1 + 2x2 ≥14 ,			(2)
		x1 ≥ 0,		x2 ≥ 0.
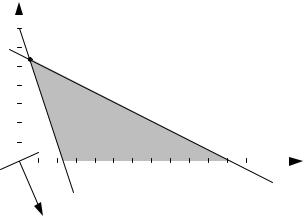
Решаем задачу ЛП графическим методом (рис.8.1):
4x1 + 8x2 = 45 : x1 = 0		→	x2	= 5,625,	x2 = 0	→	x1 = 11,25;
6x1 + 2x2 = 14 :	x1 = 0		→	x2 = 7,	x2 = 0	→	x1 = 2,33;

где ~′( ) f x

Из Точка x 0

f#′(x) = (4, −8),

− градиент целевой функции задачи ЛП.

рис. 8.1 следует, что задача ЛП имеет решение x0 . является решением системы уравнений

4x1 + 8x2 = 45,6x1 + 2x2 = 14.

75

x2

7

6

x0

5

4

3

2

1

x1

1 2 3 4 5 6 7 8 9 10 11 12

f#

(x)

(2)

(1)

Рис. 8.1

Находим x0 :

−

4x1 + 8x2

= 45 →

x = 11 = 0,55;

24x1 + 8x2

= 56

1

20

− 20x1

= −11

4 0,55 + 8x2

= 45

→

8x2 = 45 − 2,2 = 42,8 →

x2

= 5,35;

x0 = (0,55; 5,35).

Полагаем λ = 1. Вычисляем x(1):

1

x(1) = x(0)

+ λ (x0

− x(0) ) = x0 = (0,55; 5,35).

1

Проверяем условия выбора x(1) :

g1 (x(1) ) = 0,552 + 5,352

− 25 = 3,9 > 0.

Поскольку

условия

не выполняются,

то

полагаем

λ1 = λ1β = 0,7 . Вычисляем x(1):

x(1)

= (2, 4) + 0,7(0,55 − 2; 5,35 − 4) =

.

= (2, 4) + (−1,015; 0,945) = (0,985; 4,945).

Проверяем условия выбора x(1) :

g1 (x(1) ) = 0,9852

+ 4,9452

− 25 = 0,423 > 0.

	76
	Поскольку условия не выполняются, то полагаем
λ	= λ β = 0,49 . Вычисляем x(1):
1	1

x(1) = (2, 4) + 0,49(−1,45; 1,35) = (2, 4) + (−0,71; 0,66) = (1,29; 4,66) .

Проверяем условия выбора x(1) :

g1 (x(1) ) = 1,292 + 4,662 − 25 = −1,62 < 0,

g2 (x(1) ) = 1,292 −10 1,29 + 4,662 −10 4,66 + 34 = −2,12 < 0,

x(1) > 0,	x(1) > 0,
1	2

f (x(1) ) = 4 1,29 − 4,662 −12 = −28,56 < f (x(0) ) = −20.

Поскольку условия выполняются, то x(1) = (1,29; 4,66).

Проверяем условия окончания решения исходной задачи

f (x(1) ) − f (x(0) )

=

− 28,6 + 20

= 0,428 > δ1 = 0,1.

f (x(0) )

− 20

Поскольку условия не выполняются, то выполняем второй

этап.

Второй этап (вторая итерация)

Осуществляем линеаризацию исходной задачи в окрестно-

	сти точки x(1) :
	~	f ′(x(1) ) = (4;		−2 4,66) = (4; −9,32),
		= −28,56	+ (4;	−9,32),(x1 −1,29; x2 − 4,66) =
	f (x)

	= −28,56 + 4(x1 −1,29) − 9,32(x2 − 4,66) == 4x1		− 9,32x2 + 9,71;
		g′(x(1) ) = (2 1,29; 2 4,66) = (2,58; 9,32),
	~	1
		(x) = −1,62 + (2,58; 9,32),(x1 −1,29; x2	− 4,66) =
	g1

= −1,62 + 2,58(x1 −1,29) + 9,32(x2 − 4,66) = 2,58x1 + 9,32x2 − 48,4;
g′ (x(1) ) = (2 1,29 −10; 2 4,66 −10) = (−7,42; − 0,68),
2
~	=
g2 (x) = −2,12 + (−7,42; −0,68),(x1 −1,29; x2 − 4,66)

			77
	= −7,42x1 − 0,68x2 +10,62.
Составляем задачу ЛП:
		~
		f (x) = → min,
		~	(x) ≤ 0;
		g1
		~	(x)	≤ 0;
		g2
	~	x1 ≥ 0,		x2 ≥ 0.
		~		~
Подставляем f (x), g1(x),				g2 (x) :
~
f (x) = 4x1 − 9,32x2 + 9,71 → min ,
	2,58x1 + 9,32x2 ≤ 48,4 ,				(1)
	7,42x1 + 0,68x2 ≥ 10,6 ,				(2)
		x1 ≥ 0,		x2 ≥ 0.
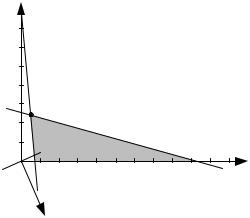
Решаем задачу ЛП графическим методом (рис. 8.2):
x2
12
10
8
6	x0
4
2
	2 4 6 8 10 12 14 16 18 (1) x1
f#	(x)	(2)
		Рис. 8.2
2,58x1 + 9,32x2 = 48,4 :		x1 = 0 → x2 = 5,2,			x2 = 0 → x1 = 18,8;
7,42x1 + 0,68x2 = 10,6 :		x1 = 0 → x2 = 15,6,			x2 = 0 → x1 = 1,43;
		~		−9,32) .
		f ′(x) = (4;

78

Из рис. 8.2 следует, что задача ЛП имеет решение x0 . Точка x0 является решением системы уравнений

2,58x1 + 9,32x2 = 48,4,7,42x1 + 0,68x2 = 10,6.

	Находим x0 :
		− 2,58x1 + 9,32x2 =		48,4		→ x =	44,7	= 4,92;
		2,58x1 + 0,236x2 =		3,7		2	9,084
			9,084x2 = 44,7
	2,58x1 + 9,32 4,92 = 48,4			→ 2,58x1 = 2,546 → x1 = 0,987;
			x0 = (0,987; 4,92).
	Полагаем λ		= 1. Вычисляем x(2):
	2
		x(2) = x(1) + λ (x0 − x(1) ) = x0 = (0,987; 4,92).
			2
	Проверяем условия выбора x(2) :
		g (x(2) ) = 0,9872		+ 4,922 − 25 = 0,181 > 0.
	1
	Поскольку		условия	не		выполняются, то полагаем
λ	= λ β = 0,7. Вычисляем x(2):
2	2

x(2) = (1,29; 4,66) + 0,7(0,987 −1,2; 4,92 − 4,66) = = (1,29; 4,66) + (−0,21; 0,18) = (1,08; 4,84).

Проверяем условия выбора x(2) :

g1(x(2) ) = 1,082 + 4,842 − 25 = −0,41 < 0,

g2 (x(2) ) = 1,082 −10 1,08 + 4,842 −10 4,84 + 34 = −0,61 < 0,

x(2)	> 0,	x(2)	> 0,
1		2

f (x(2) ) = 4 1,08 − 4,842 −12 = −31,11 < f (x(1) ) = −28,56.

Поскольку условия выполняются, то x(2) = (1,08; 4,84).

Проверяем условия окончания решения исходной задачи

79

f (x(2) ) − f (x(1) )

=

− 31,11+ 28,56

=

0,089 < δ1 = 0,1,

f (x(1) )

− 28,56

x1(2) − x1(1)

=

1,08

−1,29

=

0,163

< δ2 = 0,3,

x1(1)

1,29

x(2) − x(1)

4,84

− 4,66

2

2

=

=

0,039

< δ2 = 0,3.

x2(1)

4,66

Поскольку

условия

выполняются, то полагаем

x* x(2) = (1,08; 4,84) , f * f (x(2) ) = −31,1

и

вычисления завер-

шаются.

Ответ: x* (1,08; 4,84) ,

f * −31,1.

Задачи

1. Дана задача условной минимизации

f (x)= x2 + x

2

−16x −10x

2

→ min,

1

2

1

x2 − 6x + 4x

2

≤ 11,

1

1

exp(x1 − 3)− x1x2 + 3x2 ≤1,

x1 ≥ 0, x2 ≥ 0.

Определить методом аппроксимирующего программирования точку x(1) при x(0) = (4, 3), β = 0,25.

2. Решить методом аппроксимирующего программиро-

вания задачу условной максимизации

f (x) = x1 + x2 → max, 2x1 − x22 ≥ 1,

0,8x12 + 2x2 ≤ 9 , x1 ≥ 0, x2 ≥ 0

при â = 0,7, ä1 = 0,1, ä2 = 0,2 , x(0) = (3, 0) .

80

9. МЕТОД ШТРАФНЫХ ФУНКЦИЙ

Метод штрафных функций относится к численным методам решения задач условной оптимизации. В данном случае исходная задача условной оптимизации преобразуется в последовательность задач безусловной оптимизации путем введения штрафных функций. Рассмотрим задачу условной минимизации вида

f(x) → min,

x X = {x Rn : gi (x) ≤ 0, i = 1, r}.

На ее основе строится задача безусловной минимизации

P(x, R) = f (x) + Ω(R, g(x)) → min, x Rn ,

где P(x, R) − расширенная функция, Ω ( R , g ( x )) − штрафная функция,

R − штрафной параметр.

Задача условной минимизации f (x) заменяется последовательностью задач безусловной минимизации P(x, Rt −1) при t = 1,2,.... При этом, исходя из заданной начальной точки x[0] , находится последовательность точек x[1] , x[2] ,..., сходящаяся при

определенных условиях к решению x исходной задачи. При минимизации расширенной функции P(x, Rt −1) , t = 1,2,..., исходной

(начальной) точкой является x[t−1] , а решение задачи безусловной минимизации P(x, Rt −1) определяет точку x[t ] .

Методы штрафных функций разделяются на методы внутренней точки и методы внешней точки. Метод штрафных функций называется методом внутренней точки (внешней точки), если

все точки последовательности x[t ] , t = 0,1,2,..., являются допус-

тимыми (недопустимыми). Вид метода (внутренней или внешней точки) определяет вид штрафной функции и правило, по которому производится пересчет штрафного параметра после решения