ТЕОРИЯ ОПТИМИЗАЦИИ И Алгоритмов / Методы_оптимизации

81

очередной задачи безусловной минимизации.

Для методов внутренней точки штрафные функции должны обладать следующими свойствами:

−на большей части допустимого множества X внутренние штрафные функции близки к нулю;

−при приближении изнутри к границе допустимого множества X внутренние штрафные функции достаточно быстро возрастают.

В качестве внутренней штрафной функции часто используются логарифмическая штрафная функция

r

Ω(Rt , g(x)) = −Rt ∑ ln(−gi (x)),

i =1

а также обратная штрафная функция

r	1
Ω(Rt , g(x)) = −Rt ∑
i =1 gi (x)

Внутренние штрафные функции имеют смысл только внутри допустимого множества X, в связи с этим необходимо проверять соблюдение ограничений при решении задач безусловной оптимизации.

Для того чтобы обеспечить сходимость последовательности точек x[t ] к точке x* , в качестве последовательности Rt , t = 0,1,2,..., для методов внутренней точки следует выбирать монотонно убывающую сходящуюся к нулю последовательность положительных чисел, т.е. Rt → +0 при t → ∞ . При этом

P(x, R ) → f (x) , x[t ] → x*. Для вычисления R используется ре-
t	t
куррентное соотношение
Rt = Rt −1 c ,	t = 1,2,!,

где R0 > 0 (часто R0 = 1 ), c > 1 (часто c = 10 ).

Для методов внешней точки штрафные функции должны обладать следующими свойствами:

− во всех точках допустимого множества X внешние штрафные функции равны нулю;

82

− при выходе за пределы допустимого множества X внешние штрафные функции становятся положительными и достаточно быстро возрастают.

В качестве внешней штрафной функции часто используется штрафная функция типа квадрата "срезки"

Ω = r 2

(Rt , g(x)) Rt ∑ gi (x) .

i =1

Здесь gi (x) − "срезка" функции gi (x), определяемая следующим образом:

g (x) = gi (x), если gi (x) ≥ 0,

i0, если gi (x) < 0.

Для того чтобы обеспечить сходимость последовательности точек x[t ] к точке x* , в качестве последовательности Rt , t = 0,1,2,..., для методов внешней точки следует выбирать монотонно возрастающую последовательность положительных чисел,

т.е. Rt → ∞ при t → ∞ . Для	вычисления Rt используется
рекуррентное сооотношение
Rt = Rt −1 c,	t = 1,2,!,

где R0 > 0 (часто R0 = 1 ), c > 1 (часто c = 10 ).

Метод штрафных функций позволяет в простых случаях явно (аналитически) решить задачу условной оптимизации. Рассмотрим в качестве иллюстрации аналитического решения следующий пример.

Пример. Дана задача условной минимизации f (x) = x → min,

x ≥ 2.

Легко видеть, что решением данной задачи является точка x*=2, при этом f =2.

Рассмотрим аналитическое решение задачи: а) методом внешней точки, б) методом внутренней точки (логарифмическая штрафная функция), в) методом внутренней точки (обратная штрафная функция).

g(x)= 2 − x ≤ 0.

83

Решение. Преобразуем ограничение исходной задачи к виду g(x)≤0:

а) Метод внешней точки.

Штрафная функция типа квадрата «срезки» имеет вид

Ω(R, g(x))= R 2 − x 2.

Получаем задачу безусловной минимизации

P(x, R)= x + R 2 − x 2 → min .

При этом предполагается, что x – внешняя точка, т.е. x < 2, g(x) = 2 − x > 0.

Уравнение, определяющее стационарные точки P(x,R), имеет вид

dP	= 1− 2R 2 − x = 0.
dx

Поскольку 2 − x > 0 , то по определению «срезки» получим

2 − x = 2 − x.

Находим стационарную точку x(1)(R):

1− 2R (2 − x) = 0 → x(1) (R) = 2 −1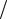(2R).

При этом

g(x(1) (R)) = 1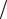(2R) > 0 при R>0,

т.е. при любом конечном R>0 соответствующая стационарная точка является недопустимой (внешней) точкой и сделанное предположение не нарушается.

Точка x*, являющаяся решением исходной задачи, опреде-

ляется следующим образом:	(R) = lim	(2 −1	(2R)) = 2.
x* = lim x(1)
R→∞	R→∞

б) Метод внутренней точки. Логарифмическая штрафная функция имеет вид

Ω(R, g(x))= −R ln(x − 2).

84

Получаем задачу безусловной минимизации

P(x, R)= x − R ln(x − 2) → min .

При этом предполагается, что x − внутренняя точка, т.е. x ≥ 2, g(x) = 2 − x ≤ 0.

Уравнение, определяющее стационарные точки P(x, R), имеет вид

dPdx = 1− x R− 2 = 0.

Находим стационарную точку x(1)(R): x(1) (R) = 2 + R.

При этом

g(x(1) (R)) = −R ≤ 0 при R ≥ 0,

т.е. при любом R≥0 соответствующая стационарная точка является допустимой (внутренней) точкой и сделанное предположение не нарушается.

Точка x*, являющаяся решением исходной задачи, опреде-

ляется следующим образом:

x* = lim x

(1)

(R) = lim (2 + R) = 2.

R→0

R→0

в) Метод внутренней точки.

Обратная штрафная функция имеет вид

R

Ω(R, g(x))= −R

1

=

.

2 − x

x

− 2

Получаем задачу безусловной минимизации

P(x, R)= x +

R

→ min .

x −

2

При этом предполагается, что x – внутренняя точка, т.е.

x ≥ 2, g(x) = 2 − x ≤ 0.

Уравнение, определяющее стационарные точки P(x, R),

имеет вид

dP

= 1−

R

= 0.

(x

− 2)2

dx

Находим стационарные точки x(1,2)(R):

85

x(1,2) (R) = 2 ± R.

При этом

g(x(1) (R)) = − R ≤ 0 при R ≥ 0,

т.е. при любом R≥0 стационарная точка x(1)(R) является допустимой (внутренней) точкой и сделанное предположение не нарушается.

С другой стороны

g(x(2) (R)) = R > 0 при R > 0,

т.е. при любом R>0 сделанное предположение нарушается, стационарная точка x(2)(R) является недопустимой (внешней) точкой и должна быть отброшена.

Решение x* исходной задачи определяется следующим об-

разом:

x* = lim x(1)	(R) = lim (2 + R ) = 2.
R →0	R →0

Алгоритм численного решения задачи условной минимизации методом штрафных функций заключается в следующем.

1. Задаются ε , δ1 , δ 2 , R0 , c и x[0] ; определяется тип x[0]

(внутренняя или внешняя); выбирается штрафная функция Ω ; строится расширенная функция P; полагается t=1.

2. Решается одним из численных методов задача безусловной минимизации

P(x, Rt −1 ) → min, x Rn.

При этом начальная точка x(0) = x[t −1] , условие окончания вычислений

P′(x(k ) , Rt −1 ) ≤ ε.

Результатом решения задачи безусловной минимизации

является точка x[t ] , в качестве которой используется оценка x(k ) точки минимума задачи безусловной минимизации.

3. Проверяется условие

t=1.

86

Если оно выполняется, то осуществляется переход к п.5. Если условие не выполняется, то осуществляется переход к

п.4.

4. Проверяются условия окончания решения исходной зада-

чи:

P(x[t ] , R

) − P(x[t −1]

, R

t−2

)

t −1

≤ δ1

,

P(x[t−1] , R

)

t−2

x[jt ] − x[jt −1]

≤ δ 2 ,

j = 1, n.

x[jt−1]

Если

они выполняются, то

полагается x* x[t] ,

f * f (x[t ] )

и вычисления завершаются.

Если условия не выполняются, то осуществляется переход

к п.5.

5. Определяется Rt , полагается t=t+1 и осуществляется

переход к п.2.

Пример. Решить методом штрафных функций задачу условной минимизации

f (x) = (x1 − 4)2 + (x2 − 4)2 → min, x1 + x2 ≤ 5

при ε = 0,2 , δ	1	= 0,4 , δ	2	= 0,1,	R = 10 ,	c = 10 , x[0] = (1,1) . Для
					0

решения задачи безусловной минимизации применить градиентный метод с дроблением шага (α = 1, β = 14) .

Решение.

Преобразуем ограничение исходной задачи к виду g(x) ≤ 0 :

g(x) = x1 + x2 − 5 ≤ 0.

Определяем тип x[0] :

g(x[0] ) = 1+1− 5 = −3 < 0.

Поскольку ограничение выполняется, то точка x[0] явля-

									87
ется внутренней (допустимой).
		Выбираем обратную штрафную функцию, т.е.
					Ω(R, g(x)) = − R g(x).
		При этом расширенная функция P(x,R) имеет вид
					P(x, R) = f (x) − R g(x).
		Первый этап
		Решаем градиентным методом с дроблением шага (МДШ)
задачу безусловной минимизации															10
		P(x, R ) = (x − 4)2 + (x							2	− 4)2 +										→ min .
			0	1										5	− x1 − x2
		Начальная точка x(0) = x[0]									= (1,1) , α = 1,							β =				1		, ε = 0,2 .
																	4
		Отметим, что в процессе решения нужно контролировать
знак штрафной функции Ω(R, g(x)) . Если окажется,																								что на k-м
шаге Ω(R, g(x)) < 0 , следует уменьшать (дробить) λk .
		Находим первые частные производные P(x, R0 ) :
	∂P	= 2(x − 4) +		10					,		∂P		= 2(x − 4) +											10				.
	∂x			(5 − x − x )2							∂x									(5 − x − x )2
		1													2
1				1			2				2													1		2
		Результаты вычислений заносим в табл. 9.1.
																							Таблица 9.1
Ном.		λ	∆x1		∆x2		x			x2			Ω		P				∂P						∂P				P′
итер.							1											∂x1							∂x2
0							1			1			3,33		21,3		−4,89							−4,89				6,92
1		1	0,707		0,707		1,71		1,71				6,33		16,82		−0,57							−0,57				0,806
2		1	0,707		0,707		2,42		2,42				62,5		67,5
			P(x (2) ) > P(x (1) ) → λ = λβ = 0,25
2		0,25	0,177		0,177		1,89		1,89				8,20		17,1
			P(x (2) ) > P(x (1) ) → λ = λβ = 0,0625
2		0,0625	0,044		0,044		1,75		1,75				6,67		16,79		−0,055							−0,055				0,078

88

Поскольку условие окончания вычислений выполнено (0,078<0,2), то вычисления завершаются. В результате решения

задачи безусловной минимизации получаем

x[1] x(2) = (1,75;1,75),

P(x[1] , R ) P(x(2) , R ) = 16,79.

0

0

Определяем

R1 = R0

c = 10 10 = 1 и

выполняем

второй

этап.

Второй этап

Решаем МДШ задачу безусловной минимизации

P(x, R ) = (x − 4)2

+

(x

2

− 4)2 +

1

→ min .

1

1

5 − x1 − x2

1

(0)

[1]

Начальная

точка

x

= x

= (1,75; 1,75) , α = 1,

β =

,

4

ε = 0,2 .

Находим первые частные производные P(x, R1 ) :

∂P	= 2(x − 4) +	1		,	∂P	= 2(x		− 4) +	1		.
∂x		(5 − x − x )2			∂x				(5 − x − x )2
	1						2
1		1	2		2				1	2

Результаты вычислений заносим в табл. 9.2.

Таблица 9.2

Ном.	λ	∆x1	∆x2	x1	x2	Ω	P			∂P			∂P			P′
итер.										∂x1			∂x2
0				1,75	1,75	0,67	10,79		−4,06			−4,06			5,74
1	1	0,707	0,707	2,46	2,46	12,5	17,24
		P(x (1) ) > P(x (0) ) → λ = λβ = 0,25
1	0,25	0,177	0,177	1,93	1,93	0,88	9,45		−3,37			−3,37			4,77
2	0,25	0,177	0,177	2,10	2,10	1,25	8,47		−2,24			−2,24			3,17
3	0,25	0,177	0,177	2,28	2,28	2,27	8,19		1,72			1,72			2,43
4	0,25	−0,177	−0,177	2,10	2,10	1,25	8,47
		P(x (4) ) > P(x (3) ) → λ = λβ = 0,0625
4	0,0625	−0,044	−0,044	2,23	2,23	1,85	8,12		−0,11			−0,11			0,156

89

Поскольку условие окончания вычислений выполнено (0,156<0,2), то вычисления завершаются. В результате решения

задачи безусловной минимизации получаем

x[2]

x(4) = (2,23; 2,23),

P(x[2] , R ) P(x(4) , R ) = 8,12.

1

1

Проверяем условия окончания решения исходной задачи

P( x[2] , R1 ) − P(x[1] , R0 )

=

8,12 − 16,79

= 0,516

> δ1

= 0,4.

P(x[1] , R )

16,79

0

Поскольку

условия не

выполняются,

то

определяем

R2 = R1 c = 1 10 = 0,1 и выполняем третий этап.

Третий этап

Решаем МДШ задачу безусловной минимизации

P(x, R

2

) = (x − 4)2 + (x

2

− 4)2 +

0,1

→ min .

1

5 − x1 − x2

Начальная

точка

x(0)

= x[2]

= (2,23;2,23) ,

α = 1, β =

1

,

4

ε = 0,2 .

Находим первые частные производные P(x, R2 ) :

∂P

= 2(x − 4) +

0,1

,

∂P

= 2(x

− 4) +

0,1

.

∂x

(5 − x − x

)2

(5 − x − x

)2

1

2

∂x

2

2

2

1

1

1

Результаты вычислений заносим в табл. 9.3.

Таблица 9.3

Ном.

λ

∆x1

∆x2

x1

x2

Ω

∂P

∂P

P′

итер.

∂x1

∂x2

0

2,23

2,23

0,185

6,45

−3,2

−3,2

4,52

1

1

0,707

0,707

2,94

2,94

−0,114

Ω(R2 , g(x)) = −0,114 < 0 → λ = λβ = 0,25

1	0,25	0,177	0,177	2,41	2,41	0,556	5,61	−0,09	−0,09	0,127

90

Поскольку условие окончания вычислений выполнено (0,127<0,2), то вычисления завершаются. В результате решения задачи безусловной минимизации получаем

x[3] x(1) = (2,41; 2,41), P(x[3] , R2 ) P(x(1) , R2 ) = 5,61.

Проверяем условия окончания вычислений исходной за-

дачи

P(x[3] , R2 ) − P(x

[2] , R1 )

=

5,61 − 8,12

= 0,309

< δ1

= 0,4,

P( x[2]

, R )

8,12

1

x[j3] − x[j2]

=

2,41 − 2,23

= 0,081 < δ2

= 0,1,

j = 1,2.

x[j2]

2,23

Поскольку

условия

выполняются,

то

полагаем

x x[3] (2,41; 2,41),

f * f (x[3] ) 5,06

и вычисления завер-

шаются.

Ответ: x* (2,41; 2,41),

f * 5,06.

Задачи

1. Дана задача условной минимизации

f (x) = (x1 − 4)2 + (x2 − 4)2 → min ,

x1 + x2 ≤ 5 .

Решить аналитически: а) методом внешней точки, б) методом внутренней точки (логарифмическая штрафная функция).

2. Дана задача условной минимизации f (x) = x1 + x2 → min ,

x12 ≤ x2 ,

x1 ≥ 1.

Решить аналитически методом внутренней точки (логарифмическая штрафная функция).