8. Циркуляция векторного поля

Вообразим, что в векторном поле имеется замкнутая линия

Циркуляцией Ц векторного поля по контуру называется величина

Циркуляция – это работа силы , совершаемая при движении вдоль

Пусть бесконечно малая площадка ограничена замкнутой ли­ниейЦиркуляцию вдольобозначим

Величина называетсяплотностью циркуляции (циркуляция на единицу площади) вокруг элементарной площадки .

9. Формула Стокса

Теорема. Если поверхность натянута на контурто

(П.9.1)

 Мысленно разобьём на кусочки и пронумеруем их. Получим кусочкиограниченные контурамиориентированными против часовой стрелки. У каждого кусочка(номер кусочка,) имеется вектор площадкигде– единичный вектор, нормальный ки согласованный с ориентацией контура(рис. 9.1).

Так как циркуляция аддитивна, то левая часть формулы (П.9.1) запишем так:

Правую часть формулы (П.9.1) запишем так:

Поэтому если докажем, что

(а)

то формула (П.9.1) будет доказана.

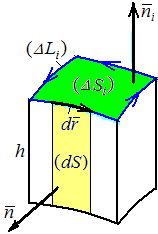
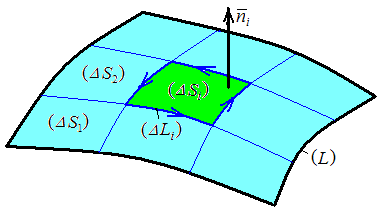
Рис. 9.1 Рис. 9.2

Построим цилиндр с основанием и высотойпараллельной(рис. 9.2). Обозначимповерхность этого цилиндра. Его объём равенпоэтомуПреобразуем левую часть формулы (а):

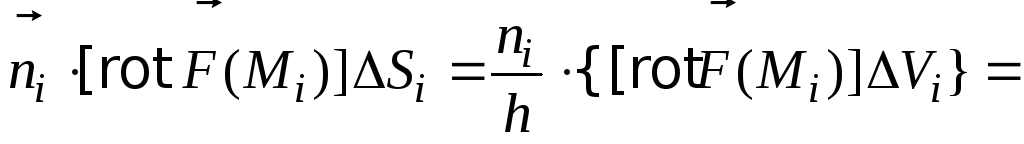(П.1.5)

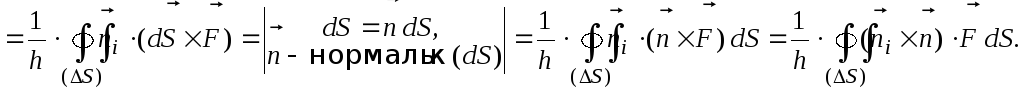
Поверхность цилиндра состоит из двух оснований и боковой поверхности. Поэтому интеграл разбивается на сумму трёх интегралов:

Следовательно,

(б)

Здесь – площадь элемента боковой поверхностиВ качествевозьмём лежащий напрямоугольник площадью(рис. 8.2), в котором– длина векторалежащего на линиии ориентированного по этой линии. Тогда

Вектор перпендикулярен обоим векторами(рис. 8.2), поэтомунаправлен вдоль единичного вектораЗначит,

В итоге равенство (б) запишется так:

Получилась формула (а), и вместе с ней формула Стокса³. ■

10. Смысл градиента, дивергенции, ротора

1. Смысл градиента:

–это вектор, направленный в сторону наискорейшего роста скаляра и по модулю равен наибольшей скорости роста .

2. Смысл дивергенции. Представим, что есть скоростьтечения некоторой жидкости. Тогда

дивергенция скорости (или) равна расходу жидкости,вытекающей через поверхность, охватывающую единичный объём:

Значит,

• если в области 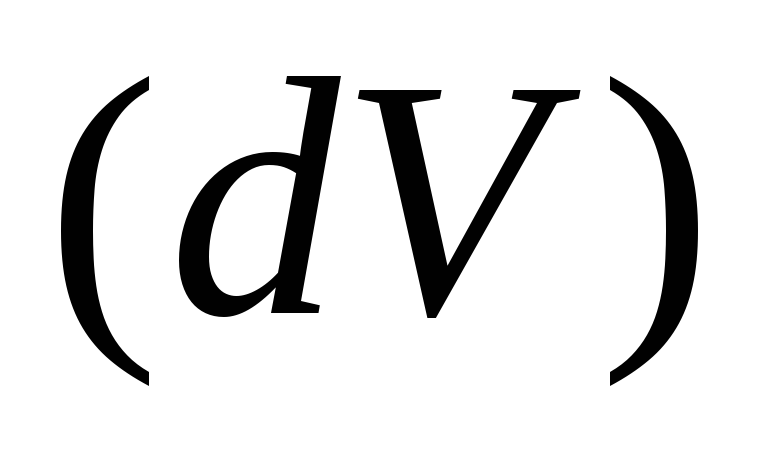имеется источник, то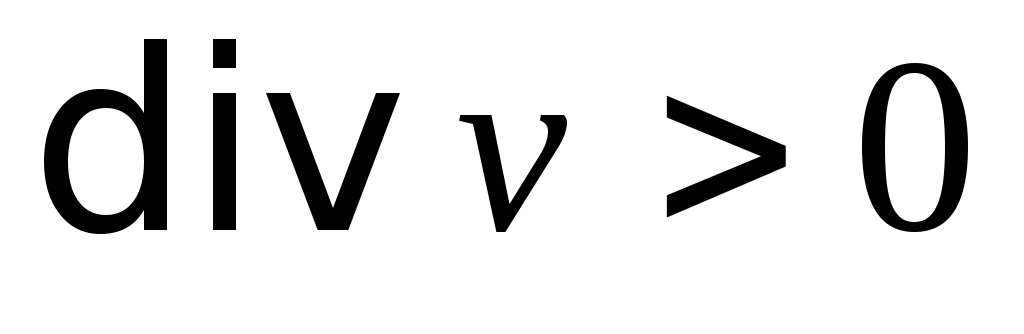(в этом случае из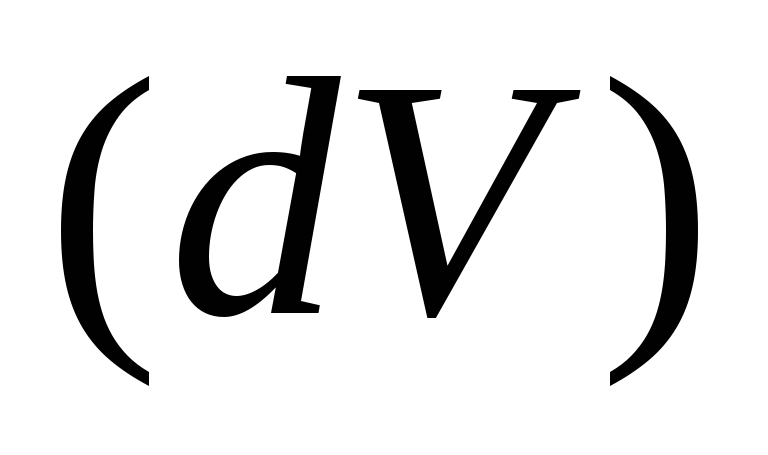жидкость вытекает);

• если в 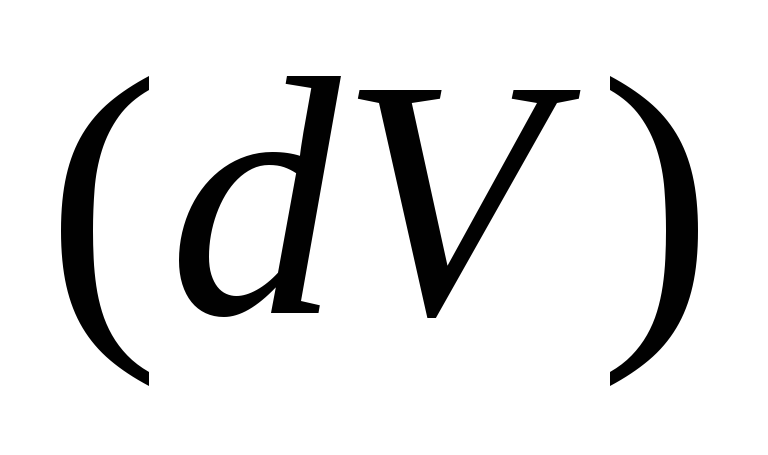имеется сток, то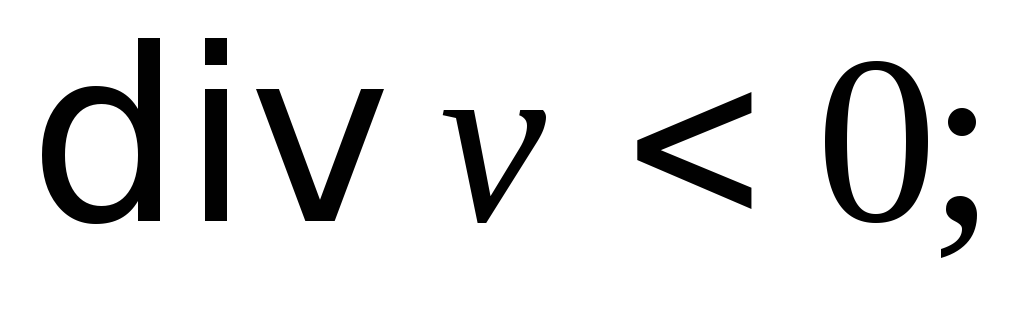

• если в нет ни стока, ни источника, то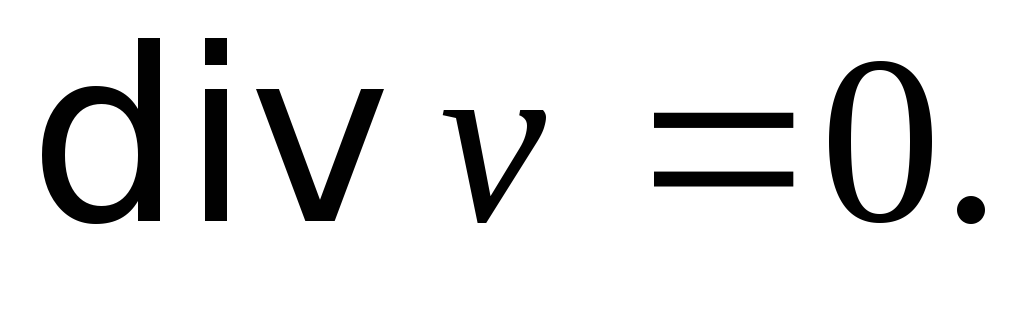

3. Смысл ротора:

–это вектор, направленный перпендикулярно площадке, вокруг которой плотность циркуляции наибольшая, причём его модуль равен этой наибольшей плотности циркуляции.

11. Закон Архимеда как следствие теоремы о градиенте

Имеется тело, занимающее область ограниченную поверхностью Тело полностью или частично погружено в покоящуюся жидкость плотности Найдём силу, действующую на тело со стороны жидкости.

На мысленно выделим бесконечно малый участок (элемент) Обозначим через давление на этом участке. Покажем, что сила давления, действующая на элемент равна Для этого воспользуемся следующими фактами. В покоящейся жидкости давление

(а) действует по перпендикуляру к площадке

(б) направлено внутрь области

И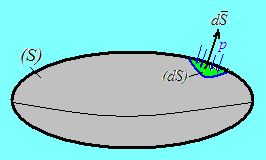з (а) следует, что давление направлено параллельно вектору площадки, где – единичный вектор, перпендикуляр­ный к и направленный наружу.

Из (б) следует, что давление направлено противоположно вектору (рис. 11.1). Значит, сила давления, действующая на элемент равна Интегри­рование этого равенства по всей замкнутой

поверхности даст суммарную силу Рис. 11.1

Воспользуемся теоремой о градиенте:

Тогда

(11.1)

Направим ось вертикально вниз. Лежащий на нём единичный вектор также будет направлен вниз. Давление внутри жидкости подчиняется закону где – давление на свободную поверхность жидкости, – глубина погружения.

Пусть тело полностью погружено в жидкость. Тогда Подстановка в (10.1) даст

где вектор направлен вверх. Получилась формула Архимеда.

Рассмотрим общий случай: тело не полностью погружено в жидкость. Область будет состоять из двух частей: часть погружённая в жидкость, и часть которая не погружена в жидкость. В таком случае

Отсюда

Подставив в (11.1), будем иметь

Получили формулу Архимеда для не полностью погружённого тела.