ОператорЫ трансляции и эволюции

Развитие состояния частицы во времени описывается волновым уравнением Шредингера. Для вывода уравнения воспользуемся оператором эволюции, сдвигающим состояние объекта во времени. Он строится по аналогии с оператором трансляции, перемещающим состояние в пространстве.

Оператор трансляции сдвигает состояние объекта на расстояниеа

. (2.44)

Для получения оператора разлагаем в ряд Тейлора по параметруa

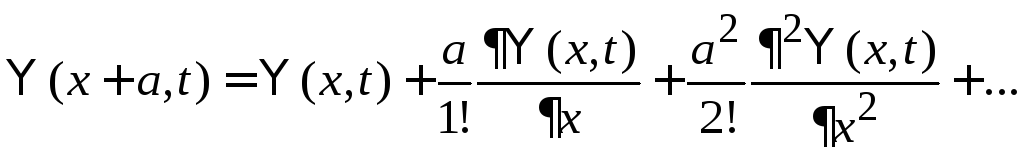
Производную по координате выражаем через оператор импульса

,

находим

,

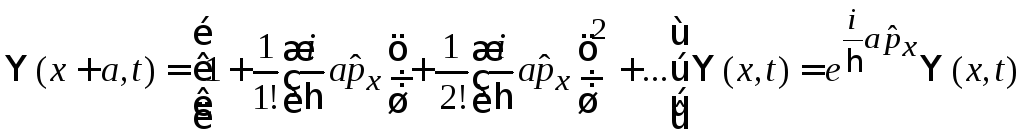где квадратная скобка является разложением в ряд экспоненты

.

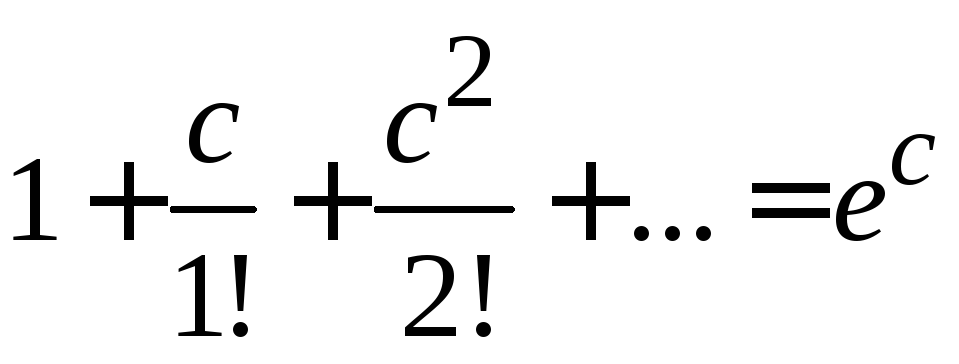В результате оператор трансляции

. (2.45)

Генератор трансляции пропорционален быстроте изменения оператора трансляции по параметру смещения вблизи нуля

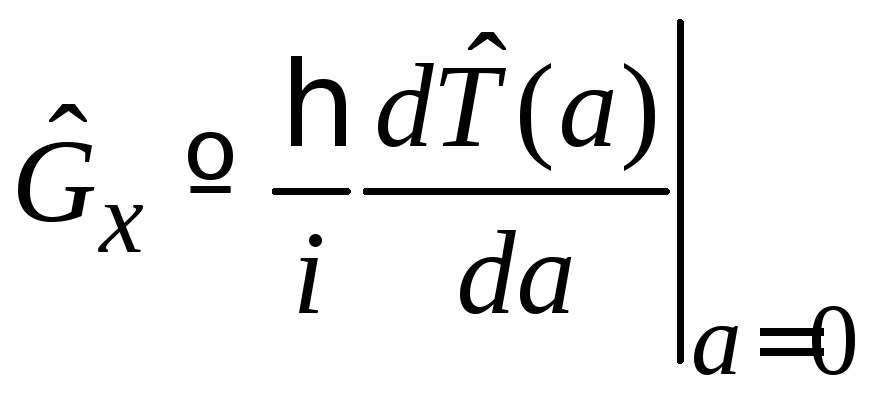. (2.46)

Определению соответствует

.

Сравнение с (2.45) дает

. (2.47)

Генератором перемещения является импульс.

Полученные результаты обобщим на смещение во времени.

Оператор эволюции передвигает состояние во времени на τ

. (2.49)

По аналогии с (2.45)

записываем

. (2.50)

Знак минус в (2.50) обусловлен разными знаками пространственного и временного слагаемых в фазе волны де Бройля (1.11)

.

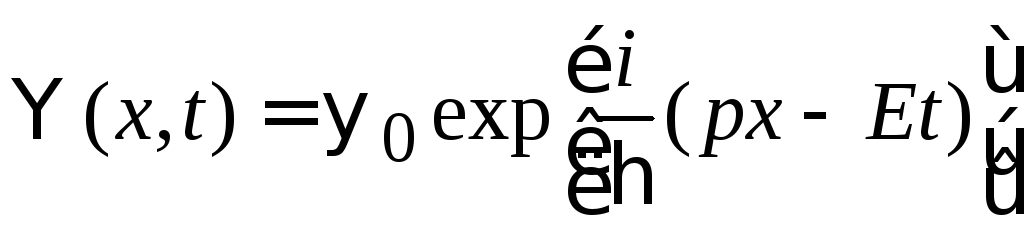В результате (2.49) получает вид

, (2.50а)

где .

Генератор эволюции, соответствующий (2.50), в виде

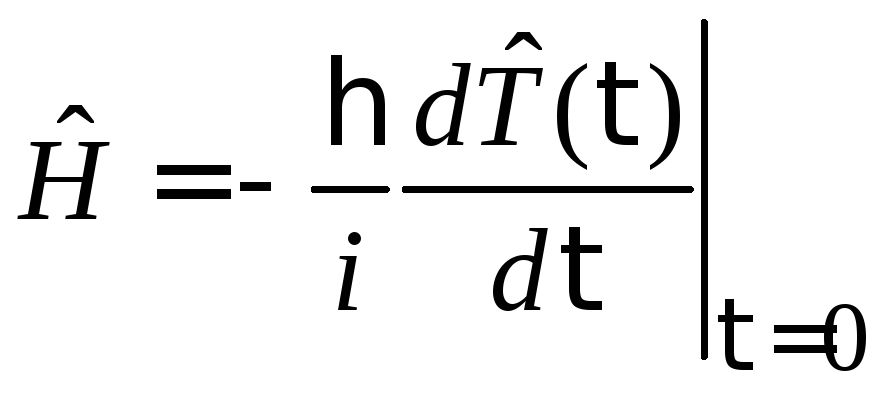(2.51)

сравниваем с генератором трансляции (2.46)

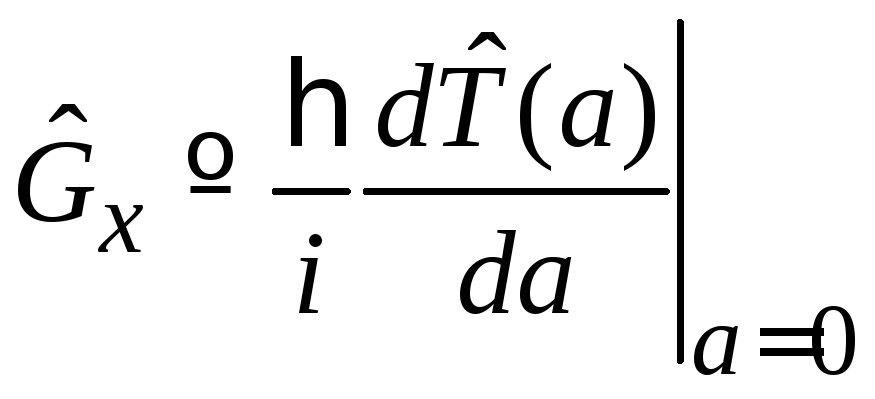
и по аналогии с (2.47)

получаем

,

в полной запаси

. (2.52)

Для установления физического смысла рассмотрим его действие на волну де Бройля

,

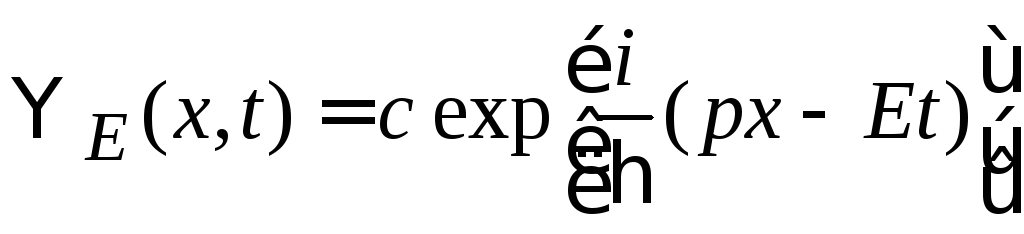описывающую частицу с полной энергией Е. Получаем уравнение

на собственную функцию оператора , где собственным значением является полная энергия. Следовательно, генератором эволюции является оператор полной энергии, или гамильтониан.

Уравнение Шредингера

Для частицы, описываемой гамильтонианом , волновая функциянаходится путем решенияволнового уравнения Шредингера, которое получил Шрёдингер в 1926 г.

Правило соответствия. При переходе от классической к квантовой теории физическим величинам сопоставляются эрмитовые операторы. При этом соотношения между динамическими характеристиками сохраняются. Это обеспечивает совпадение результатов квантовой теории при больших значениях квантовых чисел с результатами классической теории.

Оператор Гамильтона. Гамильтониан частицы в классической теории является суммой кинетической и потенциальной энергий, выраженных через импульсы и координаты:

.

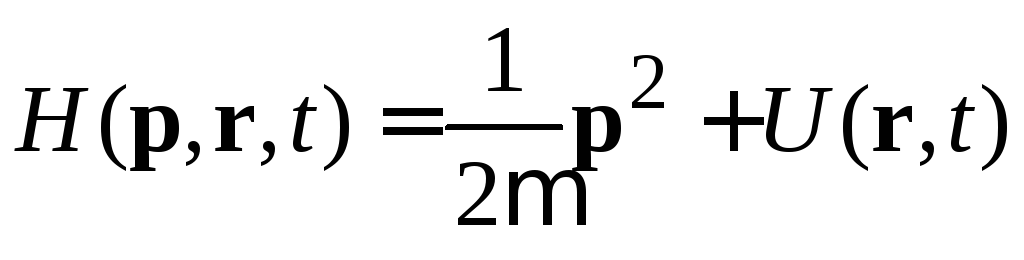Переходим к операторам

,

,

,

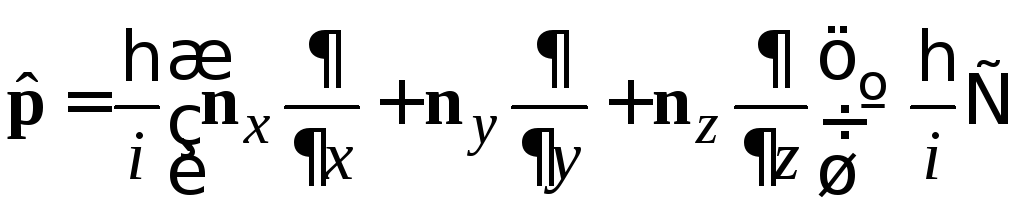где

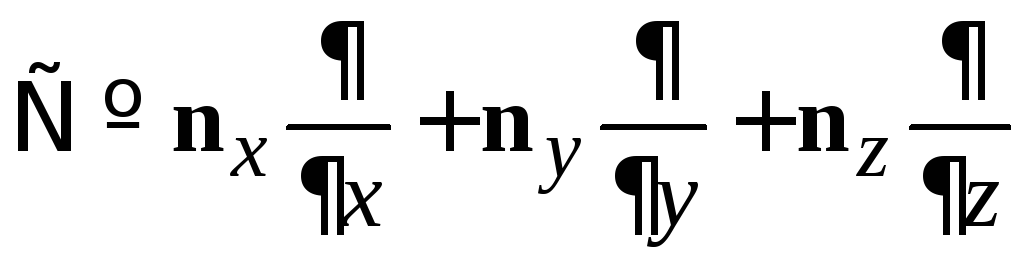–оператор градиента,

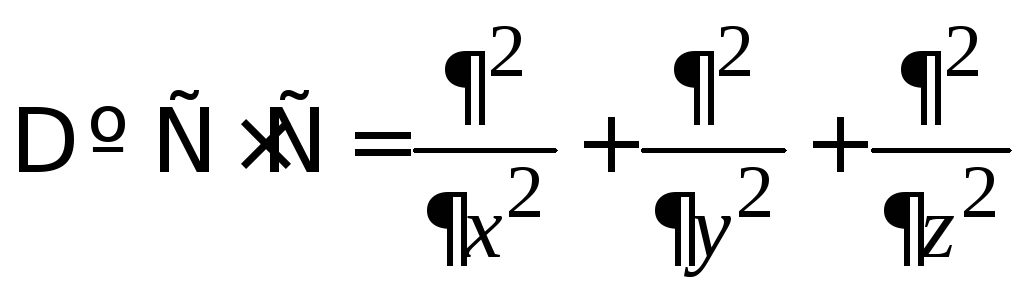–оператор Лапласа.

Получаем оператор полной энергии, или оператор Гамильтона

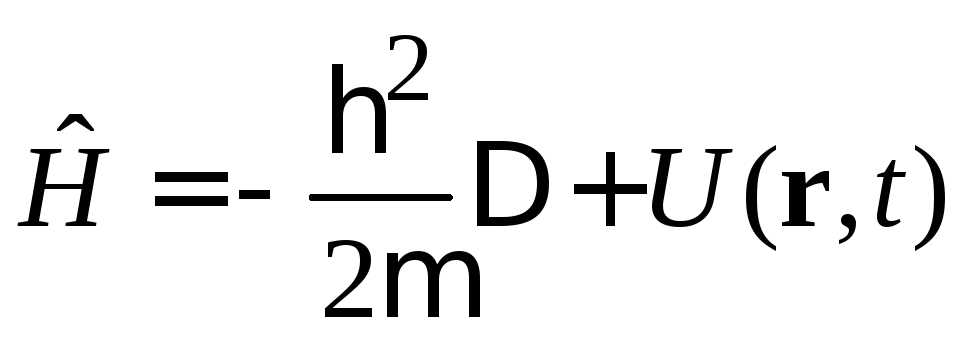. (2.53)

Волновое уравнение Шредингера. Из (2.52)

и (2.53) получаем для уравнение

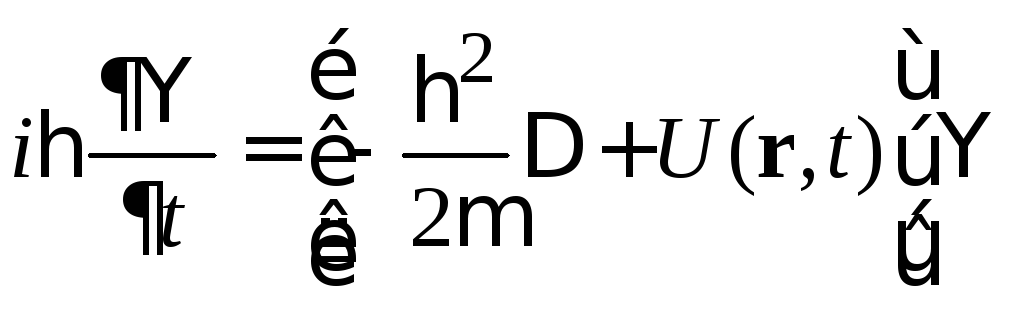. (2.54)

Стационарное уравнение Шредингера. Если потенциальная энергия не зависит от времени

,

то состояние системы стационарное, полная энергия E сохраняется и является параметром. В уравнении (2.54) слагаемые с координатами и временем разделены при , поэтому решение является произведением независимых функций от разных аргументов

. (2.55)

Подставляем (2.55) в (2.54), умножаем уравнение слева на , переменные разделяются

.

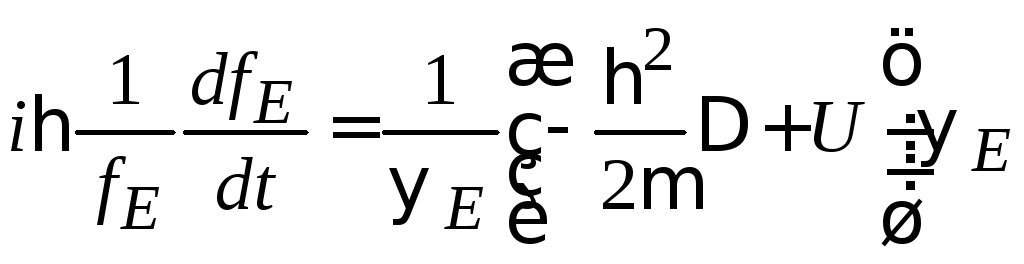Левая и правая стороны зависят от разных переменных, поэтому обе стороны равны постоянной, которую обозначим Е и далее установим ее физический смысл.

В уравнении

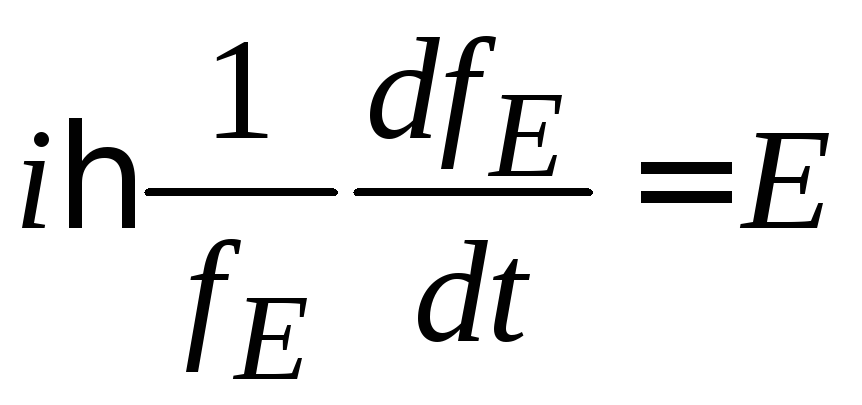
разделяем переменные

,

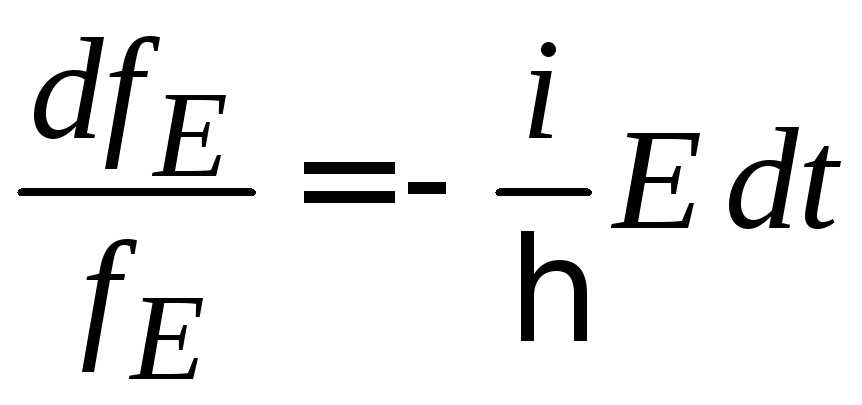интегрируем и находим

. (2.56)

Для получаемстационарное уравнение Шредингера

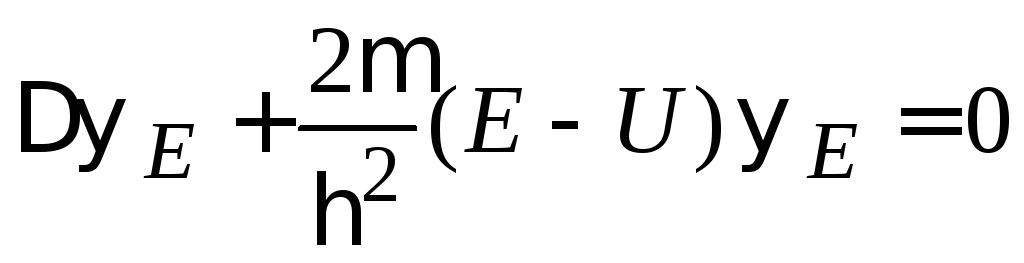. (2.57)

Уравнение (2.57) с учетом 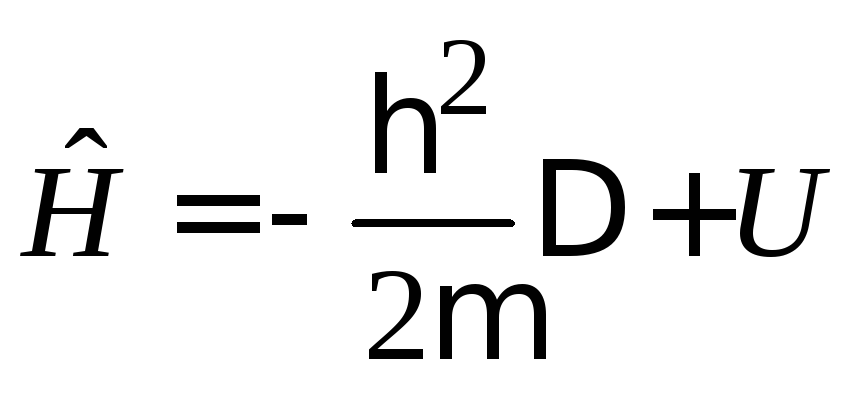является уравнением на собственную функцию оператора Гамильтона

, (2.58)

следовательно, Е – полная энергия. Если система одномерная, то (2.57) для получает вид

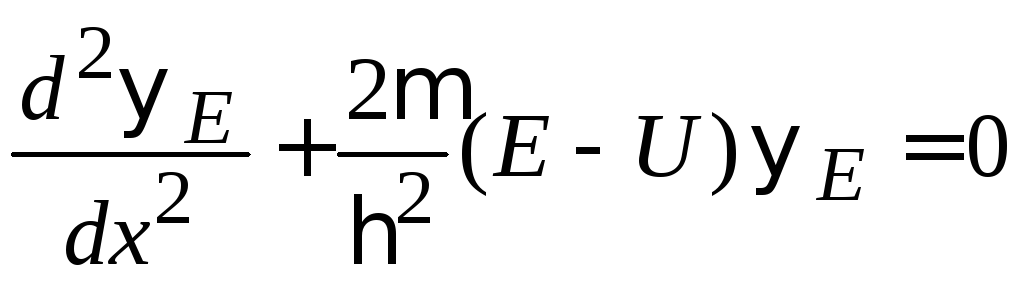. (2.59)

Уравнения (2.57) и (2.59) позволяют найти допустимые значения энергии E и соответствующие комплексные нормированные функции состояний , если заданы граничные условия.

Стационарное состояние

(2.60)

периодически зависит от времени как с частотой, пропорциональной энергии:

. (2.61)

Для свободной частицы при получаем

,

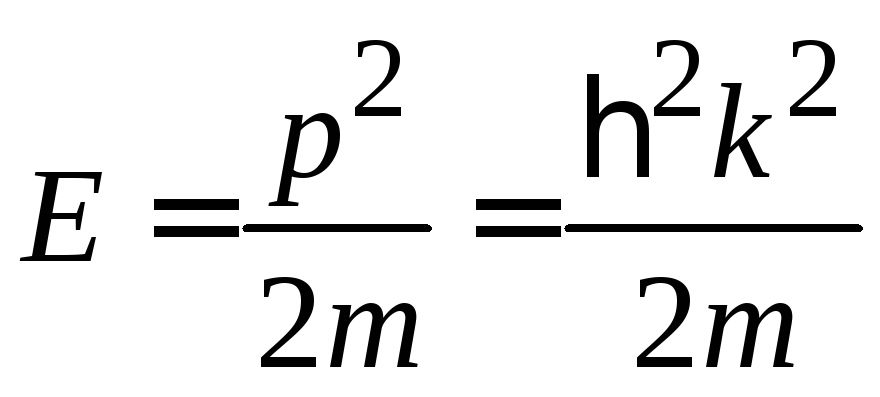и находим зависимость частоты от волнового числа – закон дисперсии

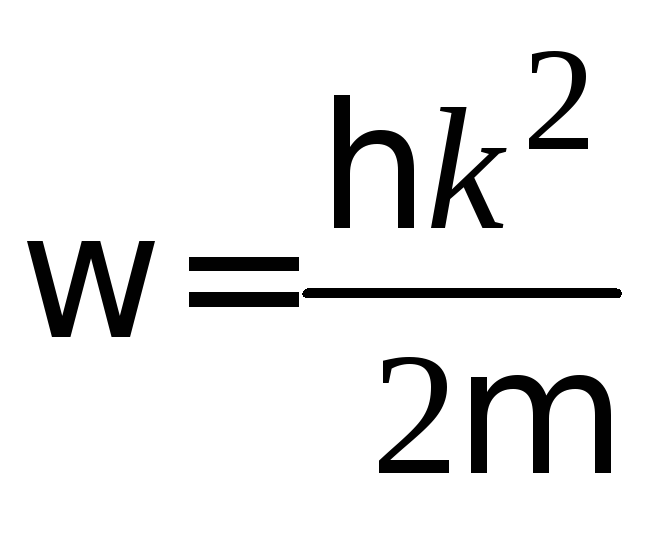. (2.61а)

Координатная часть комплексной волновой функции стационарного состояния выражается в общем случае через вещественные функции – амплитуду A и фазу β

. (2.63)

Плотность вероятности равна квадрату амплитуды

.