Informatika_met_ukazania

Рис. 15. Окно выходного графика

Первым столбцом вычисленной матрицы Y будут значения искомого тока i(t) , вторым столбцом − значения его производной i (t) . Напряжения и токи на резисторе R, индуктивности L и емкости C связаны соответственно следующими выражениями: uR (t) Ri(t) , uL (t)

L	di(t)	и	duC (t)	1		i(t) .
	dt		dt		C

Порядок выполнения работы

1.Выполнить анализ нелинейной цепи (см. рис. 1). Искомыми являются напряжения на резисторе и диоде. Исходные данные и тип интерполяционного полинома − в соответствии с вариантом. Процесс вычислений выполнить с использованием М-файл функций и/или М- файл программы. Результаты вычислений представить в графической форме.

2.Найти численное решение задачи Коши для дифференциального

уравнения 1-го порядка на отрезке [x0, x0+1]. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме.

3.Найти решение задачи Коши для системы дифференциальных уравнений 1-го порядка

51

	y	f (x, y , y		2	),		y1 (a)		y0,1 ,
	1	1	1			при начальных условиях
	y2	f2 (x, y1 , y2 )					y2	(a)	y0,2

на отрезке [a, b] с постоянным шагом h = 0.1. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме.

4. Выполнить анализ (в данном случае это поиск uR (t) , uL (t) или uC (t) во временном диапазоне от 0 и до Т) одной из схем, приведен-

ных рис. 8 (для нечѐтных вариантов − рис. 8,а, для чѐтных − рис. 8,б). Для задания начальных условий следует использовать знания, полученные при изучении курса физики. При составлении выражения для вычисления функции e(t) рекомендуется использовать известное из

аналитической геометрии уравнение прямой линии, проходящей через две заданные точки. Число разбиений временного отрезка [0, T] выбрать из диапазона 100…1000. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме.

5. Выполнить анализ (в данном случае это поиск uR (t) , uL (t) и

uC (t) или iR (t) , iL (t) и iC (t) во временном диапазоне от 0 и до Т) одной из схем, приведенных на рис. 13 (для нечѐтных вариантов −

рис. 13,б, для чѐтных − рис. 13,а). Число разбиений временного отрезка [0, T] выбрать из диапазона N = 100…1000. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме (графики uR (t) , uL (t) , uC (t) , e(t) , а также uR (t) + uL (t) + uC (t) или iR (t) , iL (t) , iC (t) , i(t) , а также iR (t) + iL (t) + iC (t) ) − четыре рисунка в одном окне.

Контрольные вопросы и задания

1.Запишите простейшие аналитические выражения, используемые

врадиотехнике для описания ВАХ диодов i(uV ) .

2.Запишите системы уравнений, используемые для нахождения коэффициентов интерполяционных полиномов.

3.Изобразите нелинейную цепь, рассмотренную в настоящей работе, и запишите описывающее ее выражение.

4.Сформулируйте задачу Коши для ОДУ 1-го и n-го порядков, а также для системы ОДУ 1-го порядка.

52

5.Сформулируйте теорему о существовании и единственности решения ОДУ 1-го порядка.

6.Как решается в системе MatLab ОДУ n-го порядка?

7.Изобразите простейшие электронные цепи, анализ переходных процессов в которых может быть выполнен с использованием ОДУ 1-го порядка. Запишите уравнения, описывающие эти цепи.

8.Изобразите простые электронные цепи, анализ переходных процессов в которых может быть выполнен с использованием ОДУ 2-го порядка. Запишите уравнения, описывающие эти цепи.

Лабораторная работа № 4

ПРИМЕНЕНИЕ ИНТЕРПОЛЯЦИОННЫХ МЕТОДОВ ДЛЯ ПРИБЛИЖЕНИЯ ВАХ ТРАНЗИСТОРА

Цель работы – ознакомление с особенностями выполнения интерполяции и сплайн-интерполяции с использованием системы

MatLab.

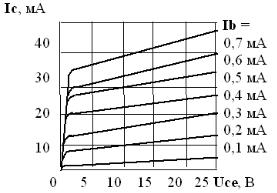
Рис. 1. Выходная ВАХ транзистора типа КТ312Б

Базовыми при проектировании многих радиотехнических устройств на транзисторах является его выходная Ic(Uce, Ib) вольтамперная характеристика (ВАХ), показанная на рис. 1, где Ib – ток базы, Uce – напряжение коллектор–эммитер, Ic – ток коллектора. Поэтому вопросы приближения этих характеристик являются весьма актуальными в инженерной практике.

53

Интерполяция таблично заданной функции одной независимой переменной

В практике вычислений часто требуется определить значение функции f(x), определенной своими значениями f(x0), f(x1), …, f(xn) на определенном наборе точек (узлов) a x0 x1 ... xn b в некоторой

промежуточной точке x (xi , xi 1) , где i = 0, 1, …, n–1. Построение

функции F(x), позволяющей вычислить значение функции f(x) в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции одной переменной. При этом f(x) называют интерполируемой, а F(x) – интерполирующей функциями. Определение значения функции f(x) для x < a или x > b называется задачей экстраполяции. При решении этих двух задач для неравноотстоящих узлов часто используются интерполяционная формула Лагранжа

n		n		x	x j
L(n, x)	f (x )					.
	i		0 xi		x j
i 0	j
	j		i

С помощью этой формулы можно выполнить интерполяцию одной из ветвей выходной (например, для Ib = 0,3 мА) ВАХ.

Интерполяция таблично заданной функции двух независимых переменных

Предположим, что на некотором наборе узлов на плоскости таблично задана функция двух независимых переменных f(x, y), опреде-

ленная своими значениями f(x0, y0), f(x1, y1), f(x2, y2)…, f(xn, yn). Примерами функций двух переменных может служить, представленная на

рис. 1 зависимость Ic(Uce, Ib). Построение функции F(x, y), позволяющей вычислить значение функции f(x, y) в точках, не совпадающих с заданным набором узлов, называется задачей интерполяции функции двух переменных. При этом f(x, y) называют интерполируемой, а F(x, y) – интерполирующей функциями. Для интерполяции таблично заданной на прямоугольной (k + 1)*(m + 1) сетке узлов функции двух независимых переменных можно использовать, например, интерполяционную формулу Лагранжа. Однако при применении интерполяционных полиномов для выполнения интерполяции возможно явление волнистости, при котором значение интерполирующей функции между узлами сколь угодно сильно отличается (осциллирует) от значений

54

интерполируемой функции в близлежащих узлах. Это является свойством степенного полинома.

Так как явление волнистости не проявляется для полиномов степени три и менее, для его преодоления используют линейную, квадратичную или кубическую сплайн-интерполяцию.

Сплайн-интерполяция

Функция одной переменной S(x), заданная на отрезке [a, b], называется сплайном порядка p, если она:

1) на каждом из частичных отрезков [xi , xi 1] [a, b] , i = 0, 1, …, n–1

является полиномом заданной степени			p 2 , т. е. может быть записана
как
		p		p
S(x) S	(x)	a(i ) (x x )k		C(i ) xk .
i		k	i	k
	k	0		k 0

2) р–1 раз непрерывно дифференцируема на [a, b]. При сплайнинтерполяции интерполируемая функция представляется набором полиномов первой, второй или третьей степени соответственно – своим для каждого из внутренних подотрезков [xi , xi 1] [a, b] .

Для реализации одномерной сплайн-интерполяции в системе MatLab имеются следующие функции:

interp1(X,Y,х, method ) – возвращает вектор, содержащий элементы, соответствующие элементам вектора х. Сплайн строится по двум входным векторам – X и Y. Параметр method (его можно опустить) определяет метод интерполяции: linear − если используется ку- сочно-линейная; spline − если интерполирование выполняется кубическими сплайнами. Пусть, например, требуется выполнить сплайнинтерполяцию таблично заданной функции

xi	1	2	4	6	7
f (xi )	1	2	5	2	0.5

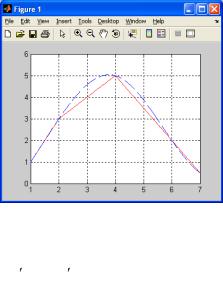
Пример реализации задачи представлен ниже, а график сплайна − на рис. 2.

>>X=[1;2;4;6;7]; % входной вектор значений независимой

%переменной

55

>>Y=[1;3;5;2;0.5]; % входной вектор значений функции

>>x=1:0.01:7; % для этих значений надо вычислить значения

%интерполирующей функции

>>y1=interp1(X,Y,x,'linear'); % линейная сплайн-интерполяция

>>y2=interp1(X,Y,x,'spline'); % кубическая сплайн-интерполяция

>>plot(x,y1,'r-',x,y2,'b--')

>>grid on

Рис. 2. Окно выходного графика

Для реализации двумерной сплайн-интерполяции в системе MatLab имеется следующая функция:

interp2(X,Y,Z,х,y, method ) – возвращает матрицу, содержащую элементы, соответствующие элементам векторов х и y. Сплайн строится по трем входным векторам – X и Y, которые содержат значения независимых переменных и Z − значения интерполируемой функции. Векторы X и Y должны быть монотонными (т. е. значения их элементов или строго возрастают или строго убывают с ростом индексов). Параметр method (его можно опустить) определяет метод интерполяции: bilinear − если используется кусочно-линейная интерполяция; bicubic − если интерполирование выполняется кубическими сплайнами.

Например, требуется выполнить сплайн-интерполяцию по следующим исходным данным (каждому столбцу матрицы Z соответствует элемент вектора X и аналогично каждой строке матрицы Z соответствует элемент вектора Y):

56

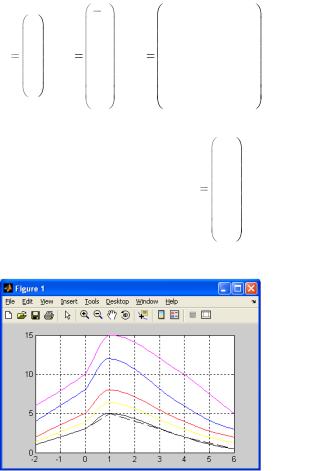
	1	2	1	2	4	6
		0	3	5	8	10
	2
X		, Y 1 , Z 5		8	12 15 ,
	4	4	2	4 6		10
	6
		6	0.5 2		3	5

при этом значения интерполирующей функции следует вычислить в

1
2
узлах прямоугольной сетки с координатами x 4	− по одной коор-
6
1.5

динате и на отрезке [–2, 6] с шагом 0.1 − по другой (назовем ее y). Реализация этого задания представлена ниже и на рис. 3.

	Рис. 3. Окно выходного графика
>> X=[1;2;4;6];	% элементы монотонно возрастают

>>Y=[-2;0;1;4;6]; % элементы монотонно возрастают

>>Z=[[1;3;5;2;0.5] [2;5;8;4;2] [4;8;12;6;3] [6;10;15;10;5]]

Z =

1.0000 2.0000 4.0000 6.0000

3.0000 5.0000 8.0000 10.0000

5.0000 8.0000 12.0000 15.0000

57

2.0000	4.0000	6.0000	10.0000
0.5000	2.0000	3.0000	5.0000

>>x=[1;2;4;6;1.5]; % задаем вектор значений по координате х

>>y=-2:0.1:6; % задаем вектор значений по координате y

>>z1=interp2(X,Y,Z,x,y,'bilinear');

>>z2=interp2(X,Y,Z,x,y,'bicubic');

>>plot(y,z2(:,1),+'k-',y,z2(:,2),'r-',y,z2(:,3),'b-',y,z2(:,4), 'm- ',y,z2(:,5),

'y-',y,z1(:,1),'k--') >> grid on

Порядок выполнения работы

1.В соответствии с вариантом выполнить одномерную интерполяцию одной из средних ветвей выходной статической ВАХ транзистора (4–6 узлов) с использованием формулы Лагранжа и построить соответствующий график. При выборе узлов следует обязательно включить точку с координатами [0, 0], а также точку перегиба ВАХ. Процесс вычислений выполнить с использованием М-файл функций и/или М- файл программы. Результаты вычислений представить в графической форме.

2.Выяснить, имеет ли место явление волнистости при выполнении интерполяции, и найти то значение из диапазона входных данных, при котором оно проявляется больше всего. Скорректировать исходные данные, добавив в них узел из области с наибольшим уровнем волнистости и вновь выполнить п. 1. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме.

3.Выполнить одномерную сплайн-интерполяцию (линейную и кубическую) одной из средних ветвей выходной ВАХ. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме. Сделать сравнительные выводы по результатам пп. 1, 2 и 3 (о соответствии интерполирующей функции интерполируемой).

4.Выполнить двумерную сплайн-интерполяцию (линейную и кубическую) для выходной ВАХ. Процесс вычислений выполнить с использованием М-файл функций и/или М-файл программы. Результаты вычислений представить в графической форме. Сделать сравнительные выводы по результатам двумерной сплайн-интерполяции (о соответствии интерполирующей функции интерполируемой).

58

ЛИТЕРАТУРА

1.Дьяконов В.П. Компьютерная математика. Теория и практика. –

М.: Нолидж. 1999 (или 2001). − 1296 с.

2.Ануфриев И.Е. Самоучитель MatLab 5.3/6.x. − СПб.: БХВ-

Петербург, 2004. − 736 с.

3.Мартынов Н.Н., Иванов А.П. MATLAB 5.x. вычисления, визуа-

лизация, программирование. − М.: КУДИЦ-ОБРАЗ, 2000. − 336 с.

4.Аносов В.Н., Наумов В.В. Программа MatLab 6.5 / Simulink 5:

учеб. пособие − Новосибирск: Изд-во НГТУ, 2007. − 104 с.

5.Вербжицкий В.М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения) − М.: Высшая школа, 2001. − 382 с.

6.Матвеев Н.М. Обыкновенные дифференциальные уравнения: учеб. пособие – СПб.: Спец. лит-ра, 1996. − 371 с.

7.Эдвардс Ч.Г., Пенни Д.Э. Дифференциальные уравнения и краевые задачи: моделирование и вычислении с помощью Mathematica, Maple и MATLAB. 3-е изд.: Пер. с англ. − М., 2008. − 1104 с.

8.Ануфриев И.Е., Смирнов А.Б., Смирнова Е.Н. MATLAB 7. −

СПб.: БХВ-Петербург, 2005. − 1104 с.

9.Кетков Ю.Л., Кетков А.Ю., Щульц М.М. MATLAB 7: програм-

мирование, численные методы. − СПб.: БХВ-Петербург, 2005. − 752 с.

59

ИНФОРМАТИКА Часть II

Методические указания

Редактор Т.П. Петроченко

Выпускающий редактор И.П. Брованова Компьютерная верстка Л.А. Веселовская

___________________________________________________________________________________

Подписано в печать 25.08.2009. Формат 60 × 84 1/16. Бумага офсетная. Тираж 150 экз. Уч.-изд. л. 3,48. Печ. л. 3,75. Изд. № 112. Заказ № Цена договорная

___________________________________________________________________________________

Отпечатано в типографии Новосибирского государственного технического университета

630092, г. Новосибирск, пр. К. Маркса, 20