
Красоленко_Сванидзе_Якунина_Теория вероятностей_2013
.pdfМинистерство образования и науки Российской Федерации
Санкт-Петербургский государственный архитектурно-строительный университет
Общестроительный факультет
Кафедра математики
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Рабочая программа, методические указания и контрольные задания
Санкт-Петербург
2013
1

УДК 519.2
Рецензент канд. физ.-мат. наук, доцент Е. К. Ершов (СПбГАСУ)
Теория вероятностей: рабочая программа, методические указания и контрольные задания / сост.: Г. В. Красоленко, Н. В. Сванидзе, Г. В. Якунина; СПбГАСУ. – СПб., 2013. – 44 с.
Даются методические рекомендации по выполнению индивидуального домашнего задания (контрольной работы № 8) по курсу высшей математики «теория вероятностей». Приводятся варианты контрольных работ.
Предназначеныдлястудентовфакультетабезотрывнойформыобучения.
Ил. 4. Библиогр.: 6 назв.
Санкт-Петербургскийгосударственный архитектурно-строительныйуниверситет,2013
ВВЕДЕНИЕ
Прежде чем приступать к выполнению контрольной работы, необходимо ознакомиться с «Рабочей программой» и изучить соответствующий теоретический материал по учебникам, указанным в разделе «Рекомендуемая литература».
Во время экзаменационной сессии для студентов безотрывной формыобучениячитаютсяустановочныелекцииипроводятсяпрактические занятия, которые носят обзорный характер.
К сдаче экзамена (зачета) допускаются только те студенты, контрольные работы которых проверены и зачтены преподавателями кафедры математики.
Следует обратить внимание на оформление контрольной работы. На титульном листе должны быть указаны:
фамилия, имя, отчество; номер зачетной книжки (студенческого билета); специальность;
название дисциплины и номер контрольной работы; номер варианта.
Номер варианта, который должен выполнять студент, соответствует последней цифре номера зачетной книжки (студенческого билета). Цифре 0 (ноль) соответствует вариант № 10.
2 |
3 |

Рабочая программа курса высшей математики
Теория вероятностей
1.Испытания и события. Действия над событиями.
2.Поле событий. Условное поле событий.
3.Относительная частота и ее свойства. Вероятность как функция на поле событий. Геометрическая трактовка вероятности. Теорема сложения вероятностей.
4.Пространство элементарных исходов.
5.Классическаямодельиспытания.Классическаяформулавычисления вероятности события.
6.Условная вероятность. Теорема умножения вероятностей. Независимые события.
7.Формула полной вероятности. Теорема Байеса.
8.Понятие случайной величины. Функция распределения случайной величины и ее свойства.
9.Дискретная случайная величина.
10.Математическоеожидание дискретнойслучайной величины
иегосвойства.Дисперсиядискретнойслучайнойвеличиныиеесвойства.
11.Схема Бернулли и биномиальная случайная величина.
12.Случайная величина, распределенная по закону Пуассона.
13.Непрерывная случайная величина. Функция распределения непрерывной случайной величины. Плотность распределения и ее свойства.
14.Вычисление математического ожидания и дисперсии непрерывной случайной величины.
15.Равномерное распределение. Математическое ожидание
идисперсияслучайнойвеличины,подчиняющейсяравномерномузакону распределения.
16.Показательное распределение.
17.Нормальное распределение.
18.Законбольшихчисел.ТеоремыА.А.МарковаиП.Л.Чебышева.
19.Центральная предельная теорема.
20.Локальная и интегральная теоремы Муавра – Лапласа.
Примерный вариант контрольной работы № 8 по теме «Теория вероятностей»
Контрольная работа содержит пять задач.
1.В урне 4 белых и 3 черных шара. Наудачу извлекаются два шара. Найти вероятность следующих событий: а) оба шара белые; б) первый вынутый шар белый, второй – черный; в) извлеченные шары разного цвета.
2.Для разрушения моста достаточно попадания хотя бы одной бомбы. Найти вероятность разрушения моста, если на него сбросить две бомбы, вероятности попадания которых соответственно равны 0,6и0,7.Предполагается,чтопопаданиеоднойизбомбнезависитот попадания другой.
Третья задача (задача 3)может быть одной из двух типов за-
дач. Первый тип задач (задача 3.1) использует при решении формулу полной вероятности, второй тип (задача 3.2) – дополнительно фор-
мулу Байеса.
3.1.На склад поступают однотипные детали с трех автоматических линий. Известно, что первая линия дает в среднем 0,3 % брака, вторая – 0,2 % и третья – 0,4 %. Найти вероятность того, что наудачу взятая со склада деталь оказалась бракованной, если с первой линии поступило 1000, со второй – 2000 и с третьей – 2500 деталей.
3.2.На склад поступают однотипные детали с трех автоматических линий. Известно, что первая линия дает в среднем 0,3 % брака, вторая – 0,2 % и третья – 0,4 %. С первой линии поступило на склад 1000, со второй – 2000 и с третьей – 2500 деталей. Наудачу взятая со склада деталь оказалась бракованной. Найти вероятность того, что эта бракованная деталь поступила с первой линии.
4. Дискретная случайная величинаX задана рядом распределения:
X |
–3 |
–1 |
0 |
2 |
4 |
|
|
|
|
|
|
|
|
Р |
0,1 |
0,2 |
? |
0,3 |
0,1 |
|
|
|
|
|
|
|
4 |
5 |

Для дискретной случайной величины X найти: а) P{X = 0}; б) математическое ожидание MX и дисперсию DX; в) функцию распределения F(x); г) P{X > –1}.
Построить график функции распределения F(x).
Пятая задача (задача 5) может быть одной из следующих двух типов задач: 5.1 и 5.2.
5.1.Функция распределениянепрерывной случайнойвеличины X имеет вид
|
0, |
если |
x ≤ 0; |
|
||
|
|
|||||
|
|
|
|
π |
|
|
|
|
|
0 < x ≤ |
; |
||
F(x) = a (1−cos x), если |
2 |
|||||
|
|
|
|
|
||
|
1, |
если |
x > |
π |
, |
|
|
2 |
|||||
|
|
|
|
|
|
|
где а – параметр. |
|
|
|
|
|
|
Для непрерывной случайной величины X найти: а) значение параметра а, при котором F(x) является функцией распределения случайной величины X; б) плотность распределения f(x); в) математи-
ческое ожидание MX и дисперсию DX; г) P π ≤ X < π .
4 2
Построить графики функции распределения F(x) и плотности распределения f(x).
5.2. Плотность распределения непрерывной случайной величины X имеет вид
|
0, |
если |
|
x ≤ 0; |
|
|
|
|
|
||||
|
|
|
|
|
π |
|
|
|
если |
0 |
< x < |
; |
|
f (x) = a sin x, |
2 |
|||||
|
|
|
|
|
|
|
|
0, |
если |
|
x > |
π |
, |
|
|
2 |
||||
|
|
|
|
|
|
|
где а – параметр.
Для непрерывной случайной величины X найти: а) значение параметра а, при котором f(x) является плотностью распределения случайной величины X; б) функцию распределения F(x); в) математи-
ческое ожидание MX и дисперсию DX; г) P π4 ≤ X < π2 .
Построить графики функции распределения F(x) и плотности распределения f(x).
Приведем некоторые понятия и теоремы теории вероятностей, необходимые для решения первых двух задач.
1.Испытания и события. Теория вероятностей имеет дело
сиспытаниями,результатыкоторыхнеопределенызаранееоднозначно. Повторение таких испытаний приводит к различным результатам, предсказать которые только по известным условиямпроведения испытаниянельзя. Словоиспытаниепонимаетсякакосуществление указанных условий, объем и содержание которых должны быть описаны заранее.
Возможные результаты испытания называются событиями. Событие называется достоверным, если оно обязательно осу-
ществляется в данном испытании (сколько бы раз его ни повторяли). Событие называется невозможным, если оно никогда не осуществляетсявданномиспытании. Достоверноесобытиеобозначимбуквой U, а невозможное – символом . Остальные события будем, как правило, обозначать заглавными буквами латинского алфавита.
2.Действия над событиями. Пусть А и В – два события, свя-
занные с каким-либо испытанием.
Объединением (или суммой) двух событий А и В, связанных
содним и тем же испытанием, называется событие C, которое осуществляется тогда, когда осуществляется либо событие А, либо со-
бытие В, либо оба эти события вместе. Обозначение: C = А В.
Пересечением (или произведением) двух событий А и В, связан-
ных с одним и тем же испытанием, называется событие D, которое осуществляется только тогда, когда осуществляются события А, и В (то есть когда события осуществляются вместе). Обозначение:
D = А В.
Если А В = , то говорят, что события А и В несовместны. Событие A называетсяпротивоположнымсобытиюА,еслионо осуществляется только тогда, когда не осуществляется событие А.
6 |
7 |

3. Поле событий. Полем событий S называется совокупность событий (которые могут происходить в результате одного и того же испытания), обладающая следующими свойствами:
1)U 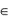 S;
S;
2)если A S, то A S ;
3)если A S и В
S и В  S, то А
S, то А  В
В 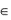 S и А
S и А  В
В  S.
S.
Из 1) и 2) вытекает, что =U S . События из поля S будем назы-
вать случайными событиями.
4. Пространство элементарных исходов. Пусть S – поле
событий,а – множество событий |
,каждоеизкоторыхпринадлежит |
полюS.Еслидвалюбыхсобытияиз |
несовместны, а каждое событие |
AS можно представить как объединения некоторого семейства
событийиз , то называетсяпространствомэлементарныхисходов.
События, принадлежащие , называются элементарными исходами.
5.Вероятностькакфункциянаполесобытий.ПустьS –поле событий, связанное с некоторым испытанием.
ВероятностьюнаполесобытийS называетсяфункция, которая каждому событию А из S ставит в соответствие число Р(А), причем так, что выполняются условия:
1) для любого A S определены неравенства 0 Р(A) 1;
2)Р( ) = 0, Р(U) = 1;
3)для любых несовместных событий А иВ изS выполняется
равенство
P(A B) = P(A)+ P(B).
|
Условие 3) называется аксиомой сложения вероятностей. |
||||||
|
Следствие, вытекающее из определения вероятностей событий: |
||||||
пусть A |
S, тогда |
|
|
|
|
|
|
|
|
|
P( |
|
) =1− P(A). |
|
|
|
|
|
A |
|
|||
|
6. Полная группа несовместных событий. Совокупность |
||||||
событий H1, H2, …, Hn из поляS, обладающая свойствами: |
|||||||
H |
|
а) события H1, H2, …, Hn попарно несовместны, то есть |
|||||
H = при i j; |
|
|
|
|
|
||
i |
j |
б) хотя бы одно из событий H |
, H , …, H осуществляется |
||||
виспытании,тоестьH1 |
1 |
2 |
n |
||||
H2 …, Hn =U, называетсяполнойгруппой |
|||||||
несовместныхсобытий. |
|
|
|||||
7. Теорема сложения вероятностей. Пусть Р – вероятность на поле событий S. Если A, B  S, то
S, то
P(A B) = P(A)+ P(B)− P(A ∩ B).
8. Условная вероятность. Пусть событие B S и Р(B) 0.
Условной вероятностью события A S при условии, что событие В произошло, называется величина
P(A / B) = P(A ∩B).
P(B)
9.Теоремаумножениявероятностей.Независимыесобытия.
Теорема. ПустьР–вероятностьнаполесобытийS.Еслисобытия А и В принадлежат полю S и Р(A)  0, Р(B)
0, Р(B)  0, то
0, то
P(A ∩B) = P(A)P(B / A) = P(B)P(A /B).
События А и В, принадлежащие полю S, называются
независимыми, если
P(A ∩B) = P(A)P(B).
10.Классическаямодельиспытания(илисхемаурн,илисхема случаев) и классическая формула вычисления вероятности события.
Определение классической модели испытания. Рассмотрим
исп ытан ие с ко н ечн ым числом исходо в = { 1, …, n}, где i –
элементарные исходы, образующие полную группу несовместных
равновероятных событий
P(ω1) = P(ω2 ) = = P(ωN ).
Так как P(ω1)+ P(ω2 )+ + P(ωN ) =1, то
P(ωi ) = |
1 |
, |
1 ≤i ≤ N . |
|
N |
||||
|
|
|
В этомслучае говорят, что испытание сводится к классической модели.
Классическая формулавычисления вероятностисобытия. Рас-
смотримвиспытании,котороесводитсяк классическоймодели, произвольное событие А, которое можно представить в виде объединения m = m(A) различных элементарных исходов, то есть
8 |
9 |

A = ωi |
ωi |
ωi |
приm N. |
1 |
2 |
m |
|
Тогда элементарные исходы ωi1 , ωi2 , ,ωim называются исходами,
благоприятствующими осуществлению события А.
Вероятность такого события находится по классическойформу-
ле вычисления вероятности
P(A) = mN(A) .
Действительно,
P(A) = P(ωi1 ωi2 ωim ) = P(ωi1 )+ + P(ωim ) = mN(A) .
При использовании классической модели испытания
предполагается следующий порядок решения задач:
1)определить элементарные исходы;
2)подсчитать количество N всех элементарных исходов;
3)событие А, вероятность которого требуется определить, представить как объединения некоторого семейства элементарных исходов из ;
4)подсчитать число m =m(A)исходов,благоприятствующих осуществлению события А;
5)воспользоваться классической формулой вычисления вероятности P(A) = m(A)/N.
11.Привычислениивероятностейчастооказываютсяполезными формулы комбинаторики. Приведем некоторые формулы этого типа.
Пустьимеетсямножествоn различныхпредметов(элементов)и
из него делаются выборки предметов (элементов)без возвращения.
Размещениями из n элементов по m называются такие соединения (выборки), которые различаются самими элементами или их порядком следования. Число всех размещений из n элементов по m
Anm = n (n −1) (n −m +1) = (n −n!m)!.
Здесь функция n-факториал определяется следующим образом:
0!=1, 1!=1, 2!=1 2, … , n!=1 2 (n −1) n.
Перестановками из n элементовназываются такие соединения, которые различаются только порядком входящих в них элементов. Число всех перестановок из n различных элементов
Pn = Ann = n (n −1) (n −m +1) 2 1 = n!.
Сочетаниями из n элементов по m называются такие их соединения, которые различаются только самими элементами, а порядком входящих в них элементов пренебрегаем. Число всех сочетаний из n элементов по m:
Cnm = |
Am |
|
n (n −1) (n −m +1) |
|
n! |
=Cnn−m . |
||
n |
= |
|
= |
|
|
|||
m! |
m! |
m!(n −m)! |
||||||
|
|
|
|
|||||
Числа Cnm называются биномиальными коэффициентами и со-
впадают с коэффициентами разложения бинома Ньютона (1 + x)n по степеням x
n
(1+ x)n = ∑Cnm xm . m=0
Для удобства полагают Cn0 =Cnn =1.
Решение задачи № 1
Эту задачу решим двумя способами. При решении задачи первым способом используются только классическая модель испытания и классическая формула вычисления вероятности события. При решении задачи вторым способом к ним добавляются аксиома сложения вероятностей и теорема умножения вероятностей.
Первый способ решения 1.а)
Пусть В = {событие, состоящее в том, что первый и второй
извлеченные шары белого цвета}.
Рассмотрим следующую классическую модель. В качестве элементарного исхода возьмем последовательность из двух извлеченныхшаров,причембудемразличатьпоследовательности(исходы)как самими элементами (шарами), так и порядком их следования (извлечения).Втерминахкомбинаторикитакиепоследовательностииздвух извлеченных шаров рассматриваются как размещения.
10 |
11 |

Тогда пространство элементарных исходов будет содержать
N = A2 |
= 7 6 = 42 |
исхода. |
7 |
|
|
Подсчитаемчислоэлементарныхисходов,благоприятствующих осуществлению события В. Последовательности, отвечающие этим исходам, надо составлять только из белых шаров (их всего четыре),
поэтому m(B) = A42 = 4 3 =12.Используяклассическуюформулувычисления вероятности события В, получаем
P(B) = mN(B) =1242 = 72 .
Замечание. При решении задачи 1.а) можно выбрать и другую классическую модель, в которой в качестве элементарного исхода взять последовательность из двух извлеченных шаров,причембудем различать эти последовательности (исходы) только самими элементами (шарами), а порядком их следования (извлечения) пренебрегаем. В терминах комбинаторики такие последовательности из двух извлеченных шаров рассматриваются как сочетания.
Классическая модель, отвечающая нашей задаче, выбирается
неоднозначно.
В новой классической модели пространство элементарных исходов содержит
N =C72 =27!5!! = 17 26 = 21 исходов.
В свою очередь число элементарных исходов, благоприятствующих появлению событию В:
m(B) =C42 = 24!!2!= 14 23 = 6.
Используя классическую формулу вычисления вероятности, получаем вновь:
P(B) = mN(B) = 216 =72 .
Пространствоэлементарныхисходов –этоматематическая модельиспытания,вкоторойлюбомусобытиюставитсянекоторое
подмножество элементарных исходов пространства . В общем случае каждому испытанию можно сопоставить несколько математических моделей, то есть пространств элементарных исходов.
Первый способ решения 1.б)
Пусть
C = {событие, состоящее в том, что первый вынутый шар белый, а второй черный}.
Для определения вероятности события C естественнее использовать первую из двух классических моделей, приведенных при решении задачи 1.а).
Тогда N = A2 |
= 7 6 = 42, m(C) = A41 A31 = 4 3 =12 |
||||
7 |
|
|
|
|
|
и |
P(C) =m(C) |
= |
4 3 |
= |
2 . |
|
N |
|
7 6 |
|
7 |
Первый способ решения 1.в)
Пусть
D={событие,состоящеевтом,чтоизвлеченыдвашараразного
цвета}.
Если использовать первую из двух классических моделей, приведенных при решении задачи 1.а), то имеем
N = A2 |
= 7 6 = 42, m(D) = A1 |
A1 |
+ A1 |
A1 |
= 4 3 +3 4 = 24 |
|||
7 |
4 |
|
3 |
3 |
|
|
4 |
|
и |
P(D) =m(D) |
=4 3 2 |
= |
4 . |
||||
|
N |
|
|
7 6 |
|
|
7 |
|
Можно использовать и вторую из двух классических моделей, приведенных при решении задачи 1.а). В результате получаем
N= C72 = 21, m(D) = C41 C31 =C31 C41 = 4 3 = 3 4 =12
иP(D) =m(ND) =74 33 =74 .
12 |
13 |

Второй способ решения 1.а)
Введем следующие события:
А1 = {первый извлеченный шар белый}; А2 = {второй извлеченный шар белый};
B ={событие, состоящее в том, что извлеченные шары белого
цвета}.
Тогда B = А1 A2. Используя теорему умножения вероятностей, получаем
P(B) = P(A1 ∩ A2 ) = P(A1)P(A2 / A1).
Найдем вероятность события А1. Всего в урне 7 шаров, среди которых 4 белых шара. Для определения вероятности P(А1) воспользуемся классическим определением вероятности
|
P(A ) = m(A1), |
|
|
1 |
N |
где m(А1) – число элементарных исходов, благоприятствующих на- |
||
ступлению события А1; N – общее число возможных элементарных |
||
исходов испытания, составляющих пространство элементарных |
||
исходов. |
|
|
В нашем случае B = 7, m(А1) = 4 |
||
и |
P(A1) = |
4. |
|
|
7 |
Найдем условную вероятность P(А2 / А1), то есть вероятность |
||
событияА2 ={второйизвлеченныйшарбелый}приусловии,чтопер- |
||
выйвынутыйшартожебелый.Здесьмывновьможемвоспользоваться классической моделью. После того как первым вынули белый шар, в урне осталось 6 шаров, среди которых 3 белых шара, и, следовательно, условная вероятность
P(A2 / A1) = 63 = 12 .
Таким образом, искомая вероятность
P(B) = P(A1 ∩ A2 ) = P(A1)P(A2 / A1) = 74 12 = 72 .
Второй способ решения 1.б)
Введем следующие события:
 А1 = {первый извлеченный шар белый};
А1 = {первый извлеченный шар белый};
B2 = {второй извлеченный шар черный};
C = {событие, состоящее в том, что первый вынутый шар белый, а второй черный}.
Тогда C = А1 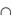 B2. И вновь, используя теорему умножения вероятностей, получаем
B2. И вновь, используя теорему умножения вероятностей, получаем
P(C) = P(A1 ∩B2 ) = P(A1)P(B2 / A1).
Вероятность события А1 была найдена в результате решения задачи 1.а).
Найдем условную вероятность P(B2 / А1), то есть вероятность события B2 = {второй извлеченный шар черный} при условии, что первый вынутыйшар белый. Здесь мы вновьможемвоспользоваться классической моделью. После того как первым вынули белый шар, в урне осталось 6 шаров, среди которых 3 черных шара, и, следовательно, условная вероятность
P(B2 / A1) = 36 = 12 .
Таким образом, искомая вероятность
P(C) = P(A1 ∩ B2 ) = P(A1)P(B2 / A1) = 74 12 = 72 .
Второй способ решения 1.в)
Введем следующие события:
А1 = {первым вынули белый шар}; А2 = {вторым вынули белый шар}; B1 = {первым вынули черный шар}; B2 = {вторым вынули черный шар};
D ={событие,состоящеевтом,чтоизвлеченыдвашараразного
цвета}.
При извлечении двух шаров разного цвета возможны две ситуации: сначала извлекают белый шар, а затем черный (событие А1 B2) или в обратном порядке: сначала извлекают черный шар, а затем белый шар (событие B1  A2). Таким образом, событие D есть объединение этих событий:
A2). Таким образом, событие D есть объединение этих событий:
D = (A1 ∩ B2 ) (B1 ∩ A2 ).
Таккак событияА1 B2 иB1 A2 несовместны, то длявычисления вероятности события D сначала воспользуемся аксиомой сложе-
ния вероятностей: вероятность объединения двух несовместных со-
14 |
15 |

бытий равна сумме вероятностей этих событий, а затем теоремой умножения вероятностей:
P(D) = P((A1 ∩ B2 ) (B1 ∩ A2 )) = P(A1 ∩ B2 )+ P(B1 ∩ A2 ) =
=P(A1 )P(B2 / A1 )+ P(B1 )P(A2 / B1 ).
При решении задачи 1.б) была найдена вероятность |
|||||||
P(A ∩B ) = P(A )P(B |
/ A ) = 4 |
1 |
= 2 . |
||||
1 |
2 |
1 |
2 |
1 |
7 |
2 |
7 |
|
|
|
|
|
|||
Аналогичным образом находится вероятность события B1 A2. |
|||||||
Если первым извлекается черный шар, то число благоприятных исходов три (в урне находятся 3 черных шара), а пространство элементарных исходов содержит семь исходов (в урне всего 7 шаров), поэтому
P(B1) = 73 .
Для нахождения условной вероятностиP(А2 /B1)вновь воспользуемсяклассическоймоделью.Послетогокак изурнывынутчерный шар, в ней остаются шесть шаров, среди которых четыре белых, и поэтому
P(A2 /B1) = 64 = 23 .
Таким образом,
P(D) = P(A1)P(B2 / A1) + P(B1)P(A2 / B1)= 74 12 + 73 23 = 74.
2
Ответ. а) Р{оба извлеченных шара белые} = 7 ; б) Р{первый
2
вынутыйшарбелый,второйчерный}= 7 ;в)Р{извлеченныедвашара разного цвета} = 74.
Решение задачи № 2
Рассмотрим следующие события:
 А1 = {первая бомба попала в цель};
А1 = {первая бомба попала в цель};
А2 = {вторая бомба попала в цель}; |
|
В |
= {мост разрушен}. |
По условию задачи события А1 и А2 – независимые события, то |
|
есть Р(А1 |
А2) = Р(А1) Р(А2), и вероятности событий А1 и А2 равны |
Р(А1) = 0,6 и Р(А2) = 0,7.
Первый способ решения задачи. Для разрушения моста достаточно попадания хотя бы одной бомбы, поэтому
B = A1 A2 .
Применим теорему сложения вероятностей
P(B) = P(A1 A2 ) = P(A1)+ P(A2 )− P(A1 ∩ A2 ).
В результате получаем
P(B) = P(A1)+ P(A2 )− P(A1)P(A2 ) = 0,6+0,7 −0,6 0,7 = 0,88.
Второй способ решения задачи. Рассмотрим событие
B ={мост не разрушен},
противоположное событию В.
Так как сумма вероятностей двух противоположных событий В и B равна единице, то есть
P(B)+ P(B) =1,
то найдем сначала вероятность события B .
Так как B = A1 ∩ A2 и события
A1 ={первая бомба не попала в цель};
 A2 ={вторая бомба не попала в цель} суть независимые события, то вероятность
A2 ={вторая бомба не попала в цель} суть независимые события, то вероятность
P(B) = P(A1 ∩ A2 ) =P(A1) P(A2 ) = (1 − P(A1)) (1 − P(A2 )).
Таким образом, P(B) = (1−0,6) (1−0,7) = 0,12 и искомая вероятность
P(B) =1− P(B) =1−0.12 = 0,88.
Ответ. Вероятность разрушения моста равна 0,88.
16 |
17 |

Решение задачи № 3.1
При решении этой задачи используется формула полной веро-
ятности.
Пусть с испытанием связана полная группа несовместных событий (гипотез) H1, …, Hn, вероятности которых не равны нулю.
Тогда вероятность появления любого события В в испытании может быть найдена по формуле
n
P(B) = ∑P(Hk )P(B / Hk ),
k =1
называемойформулойполной вероятности, где Р(Hk) –вероятности |
||
гипотезыHk и Р(B/Hk)–условнаявероятностьсобытияВприусловии, |
||
что справедлива гипотеза Hk, 1 k n. |
|
|
Перейдем к решению задачи. Пусть |
|
|
B ={событие,состоящеевтом,чтонаскладпопадаетбрако- |
||
ванная деталь}. |
|
|
Далее введем три гипотезы: |
|
|
H1 |
= {на склад поступила деталь с первой линии}; |
|
H2 |
= {на склад поступила деталь со второй линии}; |
|
H3 |
= {на склад поступила деталь с третьей линии}. |
|
НайдемвероятностигипотезH1,H2 иH3,используяклассическую |
||
модель и классическую формулу вычисления вероятности события. |
||
В качестве элементарного исхода |
будем рассматривать |
|
появление на складе отдельной детали. |
|
|
Всего на склад поступило 5500 деталей, следовательно, пространство элементарных исходов содержит N = 5500 исходов. Среди
них m(H1) = 1000 исходов благоприятствуют осуществлению гипоте- |
||||||||||||
зыH1,m(H2)=2000иm(H3)=2500исходовблагоприятствуютосуще- |
||||||||||||
ствлению гипотез H2 и H3 соответственно. Поэтому |
|
|
|
|
||||||||
P(H1) = m(H1) |
= |
1000 |
= |
2 |
, |
P(H2 ) = m(H2 ) |
= 2000 = |
|
4 |
, |
||
5500 |
|
|
|
|||||||||
N |
|
11 |
|
N |
5500 |
11 |
||||||
P(H3 ) = m(H3 ) |
= |
2500 |
= |
5 |
. |
|
|
|
|
|
||
5500 |
|
|
|
|
|
|
||||||
N |
|
11 |
|
|
|
|
|
|||||
Отметим, что гипотезы H1, H2 |
и H3 |
образуют полную группу не- |
||||||||||||||||
совместных событий и поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P(H1)+ P(H2 )+ P(H3 ) = |
|
2 |
+ |
|
4 |
+ |
|
5 |
|
=1. |
||||||||
|
|
|
11 |
|||||||||||||||
|
|
|
|
|
|
11 |
11 |
|
||||||||||
Условные вероятности Р(B /Hk), то есть вероятности события В |
||||||||||||||||||
при условии, что справедливы гипотезы Hk, 1 |
|
k |
3, известны из |
|||||||||||||||
условия задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P(B /H1) = 0,003, |
P(B /H2 ) = 0,002 и P(B /H3 ) = 0,004. |
|||||||||||||||||
Найдем вероятность события В, используя формулу полной |
||||||||||||||||||
вероятности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P(B) = P(H1 )P(B / H1 )+ P(H 2 )P(B /H 2 )+ P(H3 )P(B /H3 )= |
||||||||||||||||||
= |
2 |
0,003 |
+ |
4 |
0,002 |
+ |
5 |
0,004 ≈ 0,0031. |
||||||||||
|
|
|
||||||||||||||||
11 |
11 |
11 |
|
|
|
|
|
|
|
|
|
|
||||||
Ответ. Вероятность того, что на склад попадет бракованная деталь, Р(B)  0,0031.
0,0031.
Решение задачи № 3.2
Иногдаврезультатеиспытанияизвестно,чтонаступилонекоторое событие В, а мы хотим узнать вероятность осуществления при этом гипотезы Hk, принадлежащей полной группе несовместных событий. Ответ на этот вопрос дает следующая теорема, называемая
теоремой Байеса.
Теорема. Пусть P – вероятность на поле событий S, а собы-
тия H1, …, Hn |
принадлежат полю S и образуют полную группу не- |
||||
совместных событий. Предположим, что событие B S и кроме |
|||||
того P(B) ≠ 0, |
P(H k ) ≠ 0, 1 ≤ k ≤ n. |
|
|||
Тогда |
|
|
|
|
|
P(H |
k |
/B) = |
P(H k )P(B /Hk ) |
, где 1 ≤ k ≤ n. |
|
n |
|||||
|
|
|
|||
|
|
|
∑P(H j )P(B /H j ) |
|
|
j=1
18 |
19 |
