
Boyarshinov_ChM_T2
.pdf
|
|
|
y |
x |
16 |
|
|
Тогда последовательность |
функций k |
сходится равномерно |
к |
||||
|
|||||||
решению y(x) на отрезке [a, b]. |
|
|
|
|
|
||
Оценим модуль выражения |
|
|
|
|
|
||
x |
x |
b |
|
|
|
|
|
 yk x y x
yk x y x  yk y dt
yk y dt  yk y
yk y  dt
dt  yk y
yk y 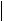 dt.
dt.
a a a
Используя неравенство17 Коши - Буняковского18, получаем:
|
b |
|
y y dt |
|
b a |
|
b |
|
y |
y |
|
2 dt |
12 |
|
|
1 2 b |
p y |
y |
|
2 dt |
1 2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 2 |
|
|
|
|
b a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
p0 |
|
k |
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 2 b |
|
p y |
y |
|
|
q y |
|
y |
|
|
|
dt |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
b a |
|
|
|
2 |
k |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
(3.40) |
|
|
|||||||||||||||||||
|
|
|
|
|
p |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В свою очередь, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yk y pyk2 qyk2 2fyk py 2 qy2 2fy dt |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
p yk2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a |
|
y 2 q yk2 y2 2f yk y dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
p yk 2 2yk y y 2 2py yk y q yk 2 2yk y y2 2qy yk y 2f yk y dt |
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
b |
|
|
|
|
|
|
|
|
y f yk y dt |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
p yk y |
q yk y |
dt 2 py yk y qy yk |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
b |
|
|
y |
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.41) |
|
|
||||||||||
|
p yk |
q yk y |
|
dt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот результат получен с учетом того, что |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
b |
|
py yk |
y qy yk y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
a |
|
|
f yk y |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
py yk y |
|
yk y py qy yk y f yk y dt |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
, |
k 12, |
, |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Согласно [10], равномерной называется сходимость последовательности операторов k |
|
|
|
|||||||||||||||||||||||||||||||||||||
оператору U по норме  Uk U
Uk U 0 рассматриваемого пространства.
0 рассматриваемого пространства.
|
|
b |
b |
|
b |
|
Неравенство Коши - Буняковского: |
a |
a |
2dx |
a |
17 |
dx |
|
2dx |
||
18 |
Буняковский Виктор Яковлевич |
[4.12.1804 |
- |
30.11.1889] - русский математик. В 1825 году защитил |
|
диссертацию на степень доктора математики. Преподавал математику и механику в 1-м кадетском корпусе, Морском корпусе, Институте путей сообщения,Петербургском университете. С 1830 года - академик Петербургской Академии наук, с 1864 - ее вице-президент. Почетный член многих русских ученых обществ и университетов.
77

b
py yk y a
b |
|
|
|
|
yk |
||||
y py |
|
qy f dt 0. |
||
a |
|
|
|
|
|
|
|
Первое слагаемое в последнем выражении обращается в нуль, поскольку минимум функционала (3.38) ищется в классе допустимых функций, удовлетворяющих граничным условиям (3.23). Второе слагаемое равно нулю вследствие выполнения исходного уравнения (3.22).
Сравнивая выражения (3.40) и (3.41), приходим к выводу, что
y x y |
|
|
|
|
1 2 |
|
y |
12 |
. |
|
x b a |
y |
|
|
|||||
|
k |
|
p |
|
|
k |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Поскольку yk x является минимизирующей последовательностью, то есть
yk y , из последнего неравенства следует, что
k
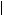 y x yk x
y x yk x  0
0
k
независимо от значения аргумента x .
Что и требовалось доказать.
78

Сеточный метод решения линейной граничной задачи
Будем считать, что линейная граничная задача (3.29) - (3.30) имеет единственное решение, непрерывное на отрезке [a, b] вместе с производными до четвертого порядка включительно.
Идея метода сеток заключается в следующем.
1. Область [a, b] задания дифференциального уравнения заменяется дискретной сеточной областью
n |
|
a k h, |
k 0,n, |
h |
b a |
|
xk |
n |
. |
||||
|
|
|
|
|
|
|
2.Граничная задача (3.29) - (3.30) заменяется сеточной задачей, то есть производные в дифференциальном уравнении заменяются разностными аналогами; в результате этого исходная задача заменяется системой алгебраических уравнений.
3.Решение системы алгебраических уравнений каким-либо численным методом позволяет определить сеточные (узловые) значения искомой функции.
Воспользуемся аппроксимацией первой и второй производных:
dy xk |
|
y xk 1 |
y xk 1 |
|
, |
dx |
|
|
2h |
|
|
|
|
|
|
||
d2 y xk |
y xk 1 2y xk y xk 1 |
||||
dx2 |
|
|
h2 |
|
|
|
|
|
|
||
и запишем разностный аналог дифференциального уравнения (3.29):
yk 1 2yk |
yk 1 |
pk |
yk 1 yk 1 |
qk yk |
fk . |
(3.42) |
h2 |
|
|
2h |
|
|
|
Очевидно, что такие соотношения можно записать для всех внутренних узлов сетки n , то есть для k 1,n 1. Поскольку в уравнениях (3.42) содержится (n + 1) неизвестное значение искомой функции, необходимо дополнить эту систему еще двумя алгебраическими уравнениями, получаемыми при замене граничных условий (3.30) разностными аналогами:
0 y0 1
0 yn 1
y1 y0 A, h
(3.43)
yn yn 1 B. h
Теперь система (n + 1) уравнений содержит ровно (n + 1) неизвестную величину.
Разрешимость системы алгебраических уравнений метода сеток
80

Для упрощения рассмотрим частный случай
0 0 1, |
1 1 0. |
Введем обзначения:
h Ak 1 2 pk ,
2Bk 2 h2qk ,
h Ck 1 2 pk ,
h yk Ak yk 1 2Bk yk Ck yk 1.
Теперь задача (3.42) - (3.43) записывается в виде
h yk fkh2 , |
k 1,n 1; |
|||||
|
|
|
|
|
|
(3.44) |
|
|
|
|
|
|
|
y |
0 |
A, |
y |
n |
B. |
|
|
|
|
|
|
||
Покажем, что соответствующая однородная система алгебраических уравнений
h zk 0, |
k 1,n 1; |
||||
|
|
|
|
|
(3.45) |
|
|
|
|
|
|
z |
0 |
0, |
z |
n |
0. |
|
|
|
|
||
имеет только тривиальное решение.
Лемма 3.1. Пусть на отрезке [a, b] заданы некоторые числа среди которых есть неравные между собой, и выполнены условия
1). |
h |
|
|
max p x 1 |
|
||
|
2 a x b |
|
, |
2). |
q x 0 |
|
|
x a,b |
|||
|
|
|
|
Y0 ,Y1,Y2 , ,Yn ,
(3.46)
а также имеет место
h Yk 0 |
k 1,n 1. |
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда |
среди |
|
чисел |
Y0 ,Y1,Y2 , ,Yn |
наибольшее |
положительное |
значение |
||||||||||
принимает либо Y0 , |
либо Yn . |
|
|
|
|
|
|
|
|
|
|
||||||
Пусть, напротив, наибольшее |
положительное |
|
значение |
Ys M 0 |
|||||||||||||
достигается внутри отрезка [a, b] |
при некотором значении 1 s n 1, причем |
||||||||||||||||
либо Ys 1 M , |
либо |
Ys 1 M . Тогда в силу условия 1) получим |
|
|
|
||||||||||||
|
h |
Y |
AY |
2B Y C Y |
A C |
M 2B |
M A C |
s |
2B |
M |
, |
|
|||||
|
s |
|
s s 1 |
|
s s |
s s 1 |
s |
s |
s |
|
s |
s |
|
|
|||
поскольку As 0, Bs 0. Благодаря условию 2) имеем:
81

|
h |
h |
ps 2 qsh |
2 |
|
M qsh |
2 |
M 0. |
h Ys 1 |
|
ps 1 |
|
|
|
|||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пришли к противоречию с исходным предположением, что и доказывает лемму.
Лемма 3.2. Пусть на отрезке [a, b] заданы некоторые числа Y0 ,Y1,Y2 , ,Yn , среди которых есть неравные между собой, выполнены условия (3.46), а также имеет место
h Yk 0 |
k 1,n 1. |
Тогда среди чисел Y0 ,Y1,Y2 , ,Yn наименьшее отрицательное значение принимает либо Y0 , либо Yn .
Доказательство этого утверждения проводится аналогично предыдущему.
Теорема 3.7. Пусть выполнены условия (3.46). тогда однородная система алгебраических уравнений (3.45) имеет только тривиальное решение.
Доказательство. В соответствии с формулами (3.45) выполнены условия лемм 3.1 и 3.2 одновременно. В этом случае наибольшим и наименьшим значениями являются либо z0 , либо zn . Но согласно формуле (3.45) z0 zn 0. Но это означает, что и все остальные zk 0, k 1,n 1. Таким образом, система уравнений (3.45) имеет только тривиальное решение, и поэтому ее определитель отличен от нуля. Следовательно, исходная система линейных алгебраических уравнений (3.44) имеет единственное решение.
Оценка порядка аппроксимации
Разложим решение задачи (3.29) - (3.30) в ряды Тейлора вблизи точки xk :
y xk 1 |
y xk y xk h y xk h2 |
y xk h3 |
yiv xk h4 |
, |
|
2 |
6 |
24 |
|
|
2 |
3 |
4 |
|
y xk 1 |
y xk y xk h y xk h2 |
y xk h6 |
yiv xk 24h |
|
Подставим эти выражения в разностный аналог (3.42) уравнения (3.29):
k y xk 1 2 y xk y xk 1 |
p xk |
y xk 1 y xk 1 q xk y xk f xk |
|||||||||||||||||||||
|
|
|
|
h2 |
|
|
|
|
|
|
|
2 h |
|
|
|
|
|
|
|
|
|||
y x |
|
yiv x |
|
h |
2 |
p x |
|
|
|
y x |
|
|
y x |
|
h |
2 |
|
|
y x |
|
f x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k |
k |
|
k |
|
k |
k |
|
q x |
k |
k |
k |
||||||||||||
|
|
12 |
|
|
|
|
|
6 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y xk p xk y xk q xk y xk f xk h2 yiv xk 2pk y xk .
12
Первое слагаемое в этом выражении совпадает с исходным уравнением (3.29) и поэтому обращается в нуль. Погрешность аппроксимации
82

|
|
2 |
|
|
k |
|
12h |
yiv xk 2pk y xk O h2 |
(3.47) |
уравнения (3.29) разностным аналогом (3.42) имеет второй порядок.
Метод прогонки для решения сеточной задачи
Запишем сеточную задачу (3.42) - (3.43) с учетом введенных ранее обозначений:
A y |
k 1 |
2B |
k |
y |
k |
C |
k |
y |
k 1 |
f |
k |
h2 |
, k 1,n 1, |
|
|||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Ah |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0h y1 1 |
0h , |
|
(3.48) |
||||||||||
y0 1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
y |
|
|
|
|
Bh . |
|
|
|||||
y |
n |
|
|
|
n 1 |
|
|
|
|
||||||||||
|
|
1 |
|
0h |
|
|
|
1 0h |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Введем соотношение |
|
|
|
|
|
||||||||||||||
yk |
uk 1yk 1 |
vk 1 , |
|
|
|
|
|
|
|
|
|
(3.49) |
|||||||
использующее дополнительные переменные |
uk ,vk , k 1,n. С помощью (3.49) |
||||||||||||||||||
запишем выражение для yk 1: |
|
|
|
||||||||||||||||
yk 1 uk yk vk uk uk 1yk 1 vk 1 vk .
Подставим два последних соотношения в уравнения (3.48):
Ak yk 1 2Bk uk 1yk 1 vk 1 Ck uk uk 1yk 1 vk 1 vk
yk 1 Ak 2Bkuk 1 Ckukuk 1 2Bkvk 1 Ckukvk 1 Ckvk fkh2 , |
k 1,n 1, |
|||||||||||||
которое будет выполняться при любом наборе значений |
yk , k 1,n 1, если |
|||||||||||||
имеют место равенства |
|
|
|
|
|
|||||||||
A 2B |
|
u |
|
|
C |
u |
u |
|
0, |
|
|
|
||
|
k |
|
k |
|
k 1 |
k |
k |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ckukvk 1 Ckvk fkh |
2 |
0, k 1,n 1, |
|
||||||||
2Bkvk 1 |
|
|
||||||||||||
Это позволяет получить рекуррентные соотношения: |
|
|||||||||||||
|
|
|
|
|
|
|
Ak |
|
, |
|
|
|
|
|
uk 1 |
2Bk |
Ckuk |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
(3.50) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fkh |
2 |
Ckvk , |
|
k 1,n 1. |
|
|
||||||
v |
k 1 |
|
|
|
|
|||||||||
|
2Bk |
Ckuk |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
Прямой ход метода прогонки выполняется в следующей последовательности действий. Запишем выражение (3.49) для k = 0
y0 u1y1 v1
и сравним с формулой
83

y |
|
|
|
1 |
y |
Ah |
|
|
|
|
0 |
|
1 0h |
1 |
1 0h |
|
|
||
сеточной задачи (3.48). |
|
|
|||||||
Отсюда можно вычислить исходные значения |
|||||||||
u |
|
|
1 |
1 |
, |
|
|
|
|
1 |
|
0h |
|
|
|
(3.51) |
|||
|
|
|
Ah . |
|
|
|
|||
v |
|
|
|
|
|
|
|||
1 |
|
1 |
0h |
|
|
|
|
||
Далее используются формулы (3.50) для вычисления всех остальных |
|||||||||
величин uk ,vk , |
k 2,n. |
|
|
||||||
Обратный ход метода прогонки. Формулу (3.49) при k = (n - 1), то есть |
|||||||||
yn 1 un yn vn , |
подставляем в последнее выражение системы (3.48): |
||||||||
yn |
|
1 |
un yn vn Bh |
0h |
, |
||||
|
|
|
1 |
0h |
|
1 |
|
||
|
|
|
|
1un |
|
1vn Bh , |
|
|
|
yn 1 |
|
|
|
||||||
|
|
|
1 0h |
1 0h |
|
|
|||
yn |
|
|
1vn Bh |
. |
|
|
|||
1 |
|
|
|
|
|||||
|
|
|
0h 1un |
|
|
||||
Теперь, используя соотношение (3.49), можно определить все искомые |
|||||||||
величины yk , |
k 0,n 1. |
|
|
||||||
Метод прогонки можно использовать в тех случаях, когда в приведенных формулах знаменатели дробей не обращаются в нули. В частности, можно избежать равенства нулю выражения ( 1 0h) в формулах (3.51) подбором соответствующего значения шага интегрирования h.
Покажем далее, что при условиях
|
A 0, |
C |
k |
0, 2B |
k |
A C |
k |
, |
k 1,n 1, |
|
|
|
||||||||||
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.52) |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
h |
1 |
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
0 |
h |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
знаменатели |
дробей |
|
2Bk |
Ckuk |
0 |
и |
1 |
0h 1un |
0. |
Оценим значения |
||||||||||||
переменных uk , |
k 1,n. Очевидно, что согласно условиям (3.52) |
|||||||||||||||||||||
u1 |
|
1 |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Предположим, |
что |
|
uk |
1 |
для произвольного значения |
k. Тогда с учетом |
|||||||||||||||
(3.52) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Bk Ckuk |
2Bk |
|
Ckuk |
2Bk |
Ck uk |
2Bk |
Ck Ak |
0, |
|
||||||||||||
84

то есть знаменатель 2Bk Ckuk отличен от нуля.
Более того, учитывая, что |
2Bk |
Ckuk Ak , |
получаем |
||
Ak |
1. |
|
|
|
|
uk 1 |
|
|
|
|
|
2B C u |
k |
|
|
|
|
k k |
|
|
|
|
|
Тем самым по индукции показано, что все |
uk 1, |
k 1,n . |
|||
Согласно условиям (3.52) |
1 |
1 0h . |
|
|
|
Тогда и знаменатель |
|
|
|
|
|
 1 0h 1un
1 0h 1un
 1 0h
1 0h
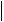 1un
1un
 1 0h
1 0h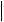
 1
1
 un
un
 1 0h
1 0h
 1
1 0
0
отличен от нуля.
Контрольные вопросы и задания
Поясните необходимость каждого из требований, предъявляемых к системам функций k и k в методах моментов, Галеркина, Ритца и наименьших квадратов.
При каких условиях полная система функций будет одновременно
замкнутой?
Решите задачу из примера 3.4 с граничными условиями с помощью системы пробных функций
1 x x 1 x,
2 x x 1 2 x,
3 x x 1 3 x,
k x x 1 k x.
Решите задачу из примера 3.5 с заданными граничными условиями, используя систему пробных функций
|
|
|
2 |
1 |
x x |
x, |
|
|
|
|
|
3
2 x x 2 x2 ,
4
3 x x x3 ,
3
|
k 1 |
|
|
||
k x x |
k |
xk . |
|
|
|
85
Выражение (3.39) в методе Ритца определяет лишь условие стационарности функционала. При каких условиях функционал yn
будет иметь единственный минимум?
Вметоде Ритца приближенное решение строится на основе функций из класса C1a,b , которые в общем случае не являются в общем случае дважды дифференцируемыми, что требуется для удовлетворения дифференциального уравнения (3.22). Поясните, в каком смысле в этом методе понимается сходимость приближенного решения к точному.
Погрешность аппроксимации (3.48) определяется не только степенью шага интегрирования h, но и ограниченностью значений производных y xk , yiv xk . Установите, при каких условиях решение уравнения (3.29) будет иметь на отрезке [a, b] ограниченные значения производных до четвертого порядка включительно.
Предложите свою разностную схему аппроксимации уравнения (3.29) и оцените ее погрешность.
Оцените порядок аппроксимации граничных условий (3.30) разностным аналогом (3.43). Предложите способ повышения порядка аппроксимации граничных условий.
Сопоставьте по эффективности метод Гаусса и метод прогонки для решения системы линейных алгебраических уравнений сеточной задачи.
Теорема 3.2 доказана для задачи (3.22) с граничными условиями (3.23). Установите условия разрешимости системы алгебраических уравнений (3.25) для задачи (3.22) с граничными условиями более общего вида (3.19).
86
