Методы и средства передачи информации (Лекция №15)

	Ar = Az cosθ,
	Aθ =− Az sinθ,
	Aα =0,
где	Az =Az ( r ) .
	Тогда, с учетом коэффициентов криволинейности координатных осей, вы-

ражения для Az ( r ) и его проекцийAr , Aθ и Aαна координатные оси, получим:

		r0			α0			θ0
	r 2 sin θ				r		r sin θ
µH = rot A = × A =		∂			∂			∂
		∂r			∂α			∂θ
		Ar		0			rAθ

= α0	1 ∂			rA	−	∂	A		=
	r		∂r	θ		∂θ	r

=α0 1

−µi(t − r v)l sin θ − r µl sin θ

− i′(t − r

v)r − i(t − r v)

+

r

4πr

4π

v r 2

r 2

+ µ

i (t − r v)

l sin θ

= α0

µ l

i′(t

− r v)

+

i(t − r v)

sin θ

4πr

vr

r 2

1

i′(t − r v)

i(t − r v)

и

Hα

=

vr

+

r 2

l sin

θ.

4π

Откуда

ε

∂Er

= rotr

−

1

∂

(r sin θ Hα )=

H

∂t

r 2 sinθ ∂θ

=

l

i′(t − r v)+ i (t − r

v) cosθ

2π

v r 2

r3

иε ∂∂Etθ = rotθH = −r sin1 θ ∂∂r (r sin θHα )=

	l		′′		′		i(t − r v)
=			v2 r	+	v r 2	+	r3	sinθ.
	4π

(15.18)

(15.19)

(15.20)

11

Интегрируя выражения (15.19) и (15.20) по времени t , получаем:

E

=

l

i (t − r v)

− q(t − r v) cosθ,

(15.21)

r

v r 2

r3

2πε

l

′

I (t − r v)

E

=

I (t − r v)

+

+ q(t − r v)

sin θ.

(15.22)

θ

v2r

v r 2

r3

2πε

Зависимость слагаемых в выражениях

E и H от r позволяет выделить

расстояния (зоны) с преобладанием тех или иных слагаемых векторов.

Зона индукции (ближняя зона) – та, где слагаемые с сомножителем ~ r13

много больше, чем другие.

Зона излучения (дальняя зона) – та, где преобладают члены с сомножите-

лем ~ 1r .

Промежуточная зона называется зоной Френеля.

Граница зон определяется не только сомножителем ~ 1r , но и скоростью

изменения тока и заряда. Влияние скорости изменения переменных удобно оценить, рассматривая случай гармонического изменения тока во времени. Это наиболее важный для практики случай.

С учетом (15.14) и (15.15) получаем

I l

k

1

−ikr

H α =

i

r

+

sin θe

,

4π

r 2

E

=

k

I l

1

−i

1

cos

θe−ikr ,

r

ω

2πε r 2

k r3

E

θ

=

k

I l

i k

+

1

−i

1

sin θe−ikr .

ω

4πε

r

r 2

k r3

12

Откуда видно, что граница r зоны индукции (ближней зоны) и дальней зоны (зоны излучения) определяется частотой поля или длиной волны λ и устанавливается соотношением r / λ.

При r << λ слагаемые, пропорциональные

1

(и, соответственно, пропор-

r 2

циональные

1

) преобладают (так как k

=

2π

<<

1

) и это – ближняя зона.

r 2

r3

r

λr

При r >> λ –

обратная картина. Поле меняется пропорционально 1

, так

r

как слагаемые пропорциональные

k =

2π

преобладают над слагаемыми про-

λr

r

порциональными

1

(и, соответственно,

1

) и это – дальняя зона.

r 2

r3

Рассмотрим подробнее свойства и структуры полей в каждой из зон. Рассмотрение начнем с анализа полей в дальней зоне, так как некоторые физически обоснованные понятия, вводимые при ее рассмотрении, затем, чисто формально, применяются и для полей в ближней зоне.

Дальняя зона:

k r >> 1.

Из анализа выражений (15.18), (15.21) и (15.22) получим:

Hα

=

l

′

4πvr

i (t − r v)sin θ,

Eθ =

l

′

i (t − r v)sin θ.

4πεv2r

Величина Er =

l

i(t − r v)cosθ по амплитуде много меньше Eθ.

2πεvr 2

Для комплексных амплитуд:

H α =i

k

I l

e−ikr

sin θ =

I&l

e−ikr sin θ,

r

2λr

4π

Eθ

=i ωµ

I l

e−ikr

sin θ = Z0

I&l

e−ikr sin θ,

4π

r

2λr

13

						E r =Z 0			I l	e −ikr cosθ,
								2	πr 2
	где	Z 0 =	ε	=	ε0	εr	– волновое сопротивление.
			µ		µ0	µr
		Заметим,			что сопротивление					Z 0 названо волновым, видимо, потому что

во-первых его размерность – Ом и для свободного пространства (точнее, вакуу-

ма, где εr =1, µr =1) оно равно 120π=377 Ом, а во-вторых, по аналогии с соот-

ношением напряжения и тока для бегущей волны в длинной линии (законом Ома для бегущей волны в «длинной линии») оно определяет связь между напряженностями электрического и магнитного полей в бегущей электромагнитной волне.

Соотношение наибольших значений электрических составляющих поля определяется выражением:

Erm (θ = 0)		λ	<<1.
	=
Eθm (θ = π 2)		πr

Из полученных выражений для полей следует, что для дальней зоны характерны следующие свойства:

1) Электрическое и магнитное поля – компоненты бегущей электромаг-

нитной волны в направлении оси r 0 . 2) Вектор Пойнтинга

Π = r0Πr = r0 (Eθ Hα ) ,

а среднее за период колебаний значение мощности, переносимой полем через замкнутую поверхность S, окружающую диполь Герца, равно:

			2π π	2	2π π	(Iml)2 r 2		3
P = ∫Πds = ∫Πr ds = ∫ ∫Πr r					sin θdαdθ = ∫ ∫ Z0	8r 2λ2	sin		θdαdθ =
S		S	α=0 θ=0		α=0 θ=0
=	πZ0	(Im2 l 2 ),							(15.23)
	3λ2

14

Эта мощность излучается (передается) диполем Герца через окружающую его замкнутую поверхность S во внешнее пространство.

3)Излучаемая мощность не зависит от радиуса сферы (площади поверхности S), что является следствием закона сохранения энергии (так как не учитываются потери в среде распространения волны).

4)Излучатель можно охарактеризовать понятием сопротивление излуче-

ния R∑ , логика введения которого следует из выражения (3.40)

R

=

P

=

2P

=

2π

Z

l 2

I 2

Im2

3

Σ

0

λ

εr

= 1

µr

= 1

Z 0

= 120π

=80π2 l 2 Ом.

λ

5)В дальней зоне магнитные силовые линии – окружности с центрами на оси диполя (т. е., как и следует из закона полного тока, они охватывают линию тока). Силовые линии электрического поля представляют собой замкнутые кривые, лежащие в меридиальных плоскостях и охватывающие магнитные силовые линии (см. рис. 15.1,а).

6)Поле максимально при θ=π/2 , то есть в плоскости, перпендикулярной оси диполя.

Для характеристики структуры излучаемых полей (т. е. полей в дальней зоне) вводят понятие диаграммы направленности.

Диаграммой направленности называют зависимость амплитуды поля от направления на источник, т. е. от координат θ и α. Для диполя E(θ, α) ~ sin θ, что в полярной системе координат соответствует окружности (см. рис. 3.5, а). Пространственная диаграмма получается вращением этой окружности вокруг оси диполя (рис. 15.5, б ), т.е. получаем «бублик без дырки».

	Ближняя зона	:	kr =	2π			r <<1 и			e−ikr ≈1.
					λ
Здесь			H α			I l		sin θ,
					4πr 2
			E r −			qlcos θ			= −i	λZ0 I l	cosθ,
						2πεr3				4π2r3

15

	E θ −	ql			sinθ=−i		λZ 0	I l	sinθ,
		4 πεr 3					8 π2 r 3
где	Z0 =	ε0 =			ε0	εr .
		µ0			µ0	µr

Итак, ближнюю зону характеризуют следующие свойства:

1) Магнитное поле определяется током, причем выражение для Hα не что иное, как формула Био-Савара для элемента постоянного тока, но с заменой по-

стоянного тока I0 на переменный i(t)=Im sin ω t.

00

θ

2700	sin θ 900
а	1800
	б

Рисунок 15.5 – Диаграмма направленности диполя Герца:

а – в плоскости, проходящей через ось диполя (полярные координаты); б – пространственная диаграмма направленности

2). Электрическое поле определяется зарядами, а выражения для состав-

ляющих Er и Eθ по форме записи совпадают с результатами расчета E по форму-

ле электростатического поля,	с заменой постоянного заряда q на переменный
заряд q = qm sin ω t. Действительно, чисто формально записав
		q		q		qlcosθ
E = −grad ϕ			−				,
	ϕ =	4 πεr1
				4 πεr2 4 πεr 2

по формуле получим приведенные выше выражения для сос-тавляющих Er и Eθ электрического поля в ближней зоне. Поэтому для идентификации полей в ближней зоне часто используют термин «квазистатические» поля.

16

Таким образом, пренебрежение запаздыванием в выражениях полей для ближней зоны приводит их к полям квазистатики (т. е. выражениям, по форме

соответствующим формулам, полученным по законам Кулона и Био-Савара).

3) Во времени магнитная Hα(t) и электрические Er(t) и Eθ(t) составляющие полей сдвинуты на π/2 (за исключением их слагаемых пропорциональных 1/r).

4) В ближней зоне (в пренебрежении составляющими векторов пропорциональными 1/r) поле – пульсирующее во времени. Вектор Пойнтинга имеет

	выраженные составляющие Πr									=[Eθ × Hα ] и	Πθ =[Er × Hα ], изменяющиеся по
	закону		sin(2ωt), а средний							за период	колебаний вектор Пойнтинга
		1 T
	Πср =		∫		Π(t)				dt ≈ 0 , т. е. можно считать, что передачи энергии в ближней зоне
		T

0

нет, а характер ее изменения колебательный.

Здесь необходимо заметить, что именно та, пренебрежимо малая в сравнении с реактивной составляющей вектора Пойнтинга, его активная составляющая и определяет режим передачи мощности излучателя (диполя) в ближней зоне, которая уже в дальней зоне определяет отличную от нуля величину средней мощности. Также необходимо понимать, что наличие потерь в среде также при-

водит к отличию от π/2 в сдвиге фаз векторов электрического и магнитного полей (пропорциональных 1/r3) в ближней зоне, что приводит к появлению активной составляющей вектора Пойнтинга в ближней зоне, ответственной за «передачу» энергии на тепловое рассеяние в окружающей среде.

5) Для ближней зоны также формально водится понятие «волновое сопро-

тивление», аналогичное по форме записи волновому сопротивлению для по-

лей в дальней зоне, т. е. отношение Eθ/Hα (или Er /Hα). Его размерность также – Ом, но оно оказывается отрицательным, чисто мнимым и равным

Z B =− j

k

=− jZ 0

1

;

ε0

′

kr

ε ωkr

Z B

= Z 0

1

>>Z 0

=

µ

0

µ r

=120π=337Ом.

kr

ε

0

εr

εr =1

µr =1

17

6) В ближней зоне силовые линии электрического поля «опираются» на заряды, а магнитные силовые линии (как и для поля в дальней зоне) представляют концентрические окружности относительно оси диполя Герца.

4. Поле плоского кругового витка с током

Круговой виток с током принято называть «рамкой с током». Рассмотрим случай, когда мгновенное значение тока i(t) на всех участках рамки в каждый момент времени одинаково. Это возможно при малости периметра рамки с током

в сравнении с длиной волны колебаний тока в ней (т. е. когда λa <<1, где а –

радиус рамки).

Ограничимся рассмотрением случая бесконечно тонкого сечения провод-

ника рамки. В этом случае в точке наблюдения M (рис. 15.6) вектор A =α0 Aα ,

так как

A коллинеарно вектору плотности тока j или элементу тока i dl рамки.

A

окружность радиуса ρ

z

Вид A

- окружность

M ρ

α0 Aα

радиуса r

а

R

θ

dl2

у

z

R

−α α

dl

α

r

а

y

dl2

dl1

dl1

dl

0

dl

dl

x

−α

x

α

а)

б)

Рисунок 15.6 – К расчету полей круговой рамки с током:

а – положение точки наблюдения в пространстве вне рамки с током;

б– проекция в плоскости рамки (по стрелке А)

При этом из выражения (15.13) получим

18

A =	µ 0 µ r	∫	i(t − R v)dl	.	(15.24)
	4π		R
		l

В соответствии с рис. 15.6, направив ось x в меридиальной плоскости, проходящей через точку наблюдения M, получим, что для симметричных относительно оси x точек рамки x-компоненты вектора А компенсируются. При этом согласно выражению (15.24) азимутальная составляющая вектора А в точке M запишется в виде

A = µ0µ r

∫

i(t − R v)dl =µ0µ r

∫

i(t − R v)d lcosα =

α

4π

R

1

4π

R

l

l

µ 0

µ r

2 πi(t −R v )

(15.25)

=

∫

acos αdα,

4

π

R

0

так как dl = a dα .

Расстояние R от элемента dl

рамки до точки M удобно выразить через

расстояние от центра рамки r. Из рис. 15.6, а видно, что

R2 = a2 + ρ2 − 2aρcos α + z2 ,

но

ρ2 + z2 = r 2 ,

ρ = rsinθ,

тогда

R2 = a2 + r 2 − 2a r sin θcosα,

(15.26)

Очевидно, непосредственное интегрирование (15.25) с учетом (15.26)

трудоем-

ко.

Рассмотрим частный случай для гармонического тока i(t). Область R << a (ближняя зона) характеризуется соотношением:

kR = 2λπ R << 2λπa <<1,

так как рассматривается рамка с радиусом а , удовлетворяющим условию

λa <<1.

Откуда e−ikR ≈1 −ikR (где i –мнимая единица) и

19

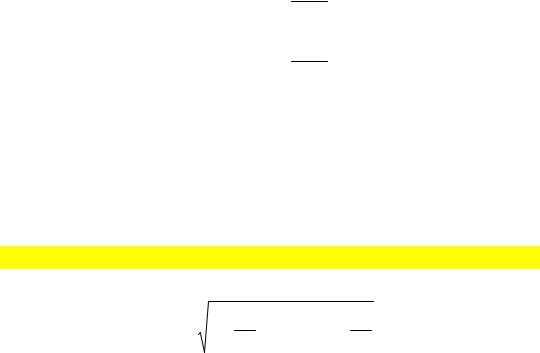
µ0 a

πcosαdα

µ0 a I π

µ0 a

πcosαdα

A ϕ =

I ∫

−ik

∫cosαdα=

I ∫

.

(15.27)

2 π

R

2

π

2 π

R

0

0

0

Формула (15.27) совпадает с выражением A для поля постоянного тока в

круговой рамке при замене I0

на I ( i ω) . Поэтому,

по аналогии с решением за-

дачи для стационарного магнитного поля

магнитное поле такой

рамки с пере-

менным током выражается в виде:

H r = Ia 2 cosθ 2 r 3

H θ = Ia 2 sinθ 4 r 3

В ближней зоне электрическое поле рамки с переменным током выражается формулой

	E ϕ =−i	ωµI a 2	sinθ.
		4r 2

Область, удаленная от витка с током на R >>a ( дальняя зона ).

	Здесь:	R = r 1 −			2a	sin θcosα +				a2	≈ r − asin θcosα,
					r					r 2
		1	=		1		≈	1	+	a	sin θcosα,
		R		r − asin θcosα				r		r 2

e−ikR e−ikr (1 + ik asinθcosα).

Тогда из (15.25) получается:

	µa	2			1			−ikr
A ϕ =			I	ik +		sinθ e
	4 r				r

20