Методы и средства передачи информации (Лекция №10)

Напряженность электрического поля определяется из уравнения Максвелла rot H αm = jωε0εr E m ,

откуда

E rm = −

1

∂H αm

=

k

C

e− j kz

=

µ0

µr

H αm

;

(10.11)

jωε0εr

∂z

jωε0εr

r

ε0 εr

Eαm = 0 ;

E zm = −

1

1 ∂

(r H

αm )= 0 .

jωε0εr r ∂z

Полученные решения (10.10) и (10.11) показывают, что в диэлектрике кабеля распространяются электромагнитные волны, векторы Е и Н которых взаимно перпендикулярны, лежат в поперечных плоскостях и образуют основную волну типа ТЕМ (поперечную электромагнитную). Они совпадают по фазе и их от-

ношение	E rm	=	µ 0	µ r	= z B .
	H αm		ε 0	ε r
Скорость распространения волны в кабеле						v =	ω	=	c	и длина вол-
							k		εr	µr

ны λ = 2π/ k определяются волновым числом k = ω/ v .

Постоянную интегрирования С можно найти исходя из того, что магнитные линии охватывают ток проводимости в жиле, проходящий через заданное поперечное сечение (например, сечение при z = 0) , или если известно напряжение между жилой и оболочкой линии в этом же сечении.

По закону полного тока I m = H αm 2πr = 2πC .

Напряжение между проводами линии

r2	r2	C	C		r2
U m = ∫E rm dr = ∫Z B r			dr =z B r	ln		.
					r1
r1	r1

11

Для того чтобы в кабеле отсутствовала отраженная волна, его необходимо нагрузить сопротивлением, равным волновому (характеристическому) сопротив-

лению кабеля: Z B

=

U m

=

z B

ln

r2

=

1 µ 0

µ r

ln

r2

.

I m

2

π

r1

2 π ε 0 ε r

r1

Как будет показано ниже, это формула совпадает с волновым сопротивле-

нием длинной линии

Z B

=

L 0

,

выраженным

через погонные ёмкость

C 0

C 0 =

2 πε0

ε r

и индуктивность

L 0

=

µ 0 µ r

ln

r2

коаксиального кабеля.

ln

r

2

2 π

r1

r1

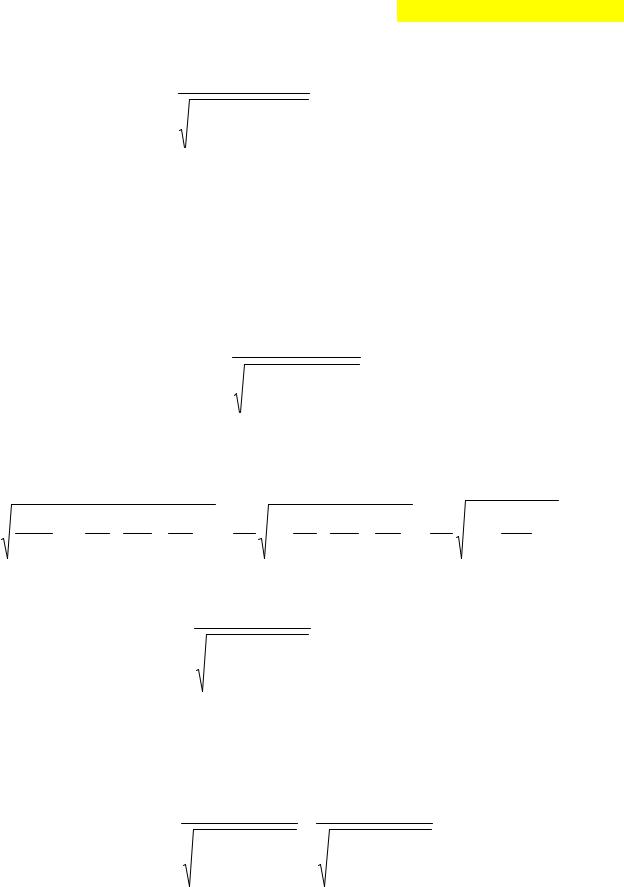
Перейдем к рассмотрению особенности распространения электромагнит-

ных волн в волноводе на примере волновода прямоугольного сечения (рис. 10,г).

Для решения этой задачи рационально выбрать декартовую систему координат, расположив оси согласно рис. 10.5 (где оси х и у лежат на внутренних поверхностях стенок). В такой системе возможны два типа волн. Сначала будем искать электромагнитное поле, ограни-

				ченное внутренней поверхностью иде-
				альных стенок волновода, через вектор-
				ный магнитный потенциал Аm, имеющий
				единственную составляющую Аzm,		кото-
				рая удовлетворяет скалярному волново-
Рисунок 10.5 − Расчетная модель				му уравнению (10.1):
				2 Azm + k 2 Azm = 0 ,
где	k = ω	−	волновое число, связанное с длиной волны источника колебаний
	c
соотношением			k = 2 π ; с − скорость света в вакууме, равная c =		1	.
			λ		ε 0	µ 0

Сразу заметим, что при неудачном исходном положении мы не сможем получить решение и тогда надо будет вновь обратиться к начальному состоянию. Заранее отметим, что мы сделали правильный выбор.

12

В декартовой системе координат волновое уравнение имеет вид

∂ 2 A zm

+

∂ 2

A zm

+

∂ 2 A zm

+ k

2

A zm = 0 .

(10.12)

∂ x 2

∂ y

2

∂ z 2

Решение этого уравнения можно найти методом разделения переменных

A zm

= X ( x ) Y ( y ) Z ( z ) .

(10.13)

Подставив (10.13) в (10.12), производя формальное дифференцирование и

деля на (10.13), получаем уравнение в полных производных:

1 ∂ 2 X

+

1

∂ 2 Y

+

1 ∂ 2

Z

+ k

2

= 0 .

(10.14)

X ∂ x 2

Y

∂ y 2

Z ∂ z 2

В этом уравнении переменные разделены, и оно распадается на три урав-

нения:

1 ∂ 2

X

= −ξ

2

;

X ∂ x 2

1 ∂ 2

Y

= −η

2

;

(10.15)

Y ∂ y 2

1 ∂ 2

Z

= −α

2

,

Z ∂ z 2

где «постоянные разделения» ξ 2 , η 2 и α 2 связаны соотношением

− ξ 2 − η 2 − α 2 + k 2 = 0,

которое удобнее рассматривать в виде

α 2 − k 2 + (ξ 2

+ η 2 ) = 0.

(10.16)

В предположении (это только предложение, и если подтвердится его правильность, то мы угадали), что в направлениях осей х и у будут иметь место стоячие волны, а в направлении оси z − бегущие волны, решение системы уравнений можно искать в виде

X = D 1 sin( ξx + ψ x ) ;

Y = D 2 sin( ηy +ψ y ) ;

Z = D 3 e − jαz + D 4 e + jαz .

13

Ограничиваясь наличием только прямой волны (т.е.. принимая D4 = 0), на основании (10.13) получим

A zm = Dsin( ξx + ψ x )sin( ηy + ψ y )e − jαz ,

(10.17)

где D = D 1 D 2 D 3 .

Постоянные разделения и постоянные интегрирования определятся из граничных условий для составляющих векторов Е и Н поля. Предварительно выра-

зим их через векторный потенциал A zm .
Напряженность магнитного поля H m = rot A m .			(10.18)
Напряженность электрического поля выразим через H m из первого урав-
нения Максвелла:
jωε 0 E m = rot H m = rot rot A m = grad div A m − 2			A m .
Но из волнового уравнения (10.1) следует, что 2 A m = − k 2 A m , поэтому
E m =	1	(grad div A m + k 2 A m ).	(10.19)
	jωε 0

Так как векторный потенциал имеет единственную составляющуюA zm , за-

висящую от всех трех координат, то уравнения (10.18) и (10.19) раскрываются следующим образом:

H xm	=	∂ A zm		;		(10.20)
			∂y
H ym	= −		∂ A zm		;	(10.21)
			∂x
H zm	= 0 .					(10.22)

Эти уравнения показывают, что в решении получилась «поперечная магнитная волна» (т.е. волна, вектор магнитного поля которой лежит в плоскости поперечной направлению распространения волны), называемая ТМволна или иначе − Е- волна, что следует из дальнейшего рассмотрения. Действительно, из

	div A m =	∂ A zm	= − jα A zm	следует
		∂z

14

E xm

=

1

grad x

div A m

= −

α

∂ A zm

=

α

H ym ;

(10.23)

ωε 0

∂x

ωε

jωε 0

0

E ym

=

1

grad y

div A m = −

α

∂ A zm

=

α

H xm ;

(10.24)

ωε 0

∂y

ωε

jωε 0

0

E zm

=

1

(grad div A m

+ k 2

A m

)= k 2 − α 2

A zm ,

(10.25)

jωε 0

jωε 0

т.е. электрическое поле имеет продольную составляющую E zm .

Интересно отметить, что в поперечных плоскостях электрическое поле имеет чисто потенциальный характер, как следует из уравнений (10.23) и (10.24). Это общее свойство всех поперечных магнитных волн, так как любой контур, лежащий в поперечной плоскости, не пронизывается магнитным полем и поэто-

му ∫E dl = 0 .

Рассмотрим граничные условия.

В силу приближения о бесконечной проводимости стенок волновода, в стенках протекает только поверхностный ток jS. Он характеризуется числом ампер, приходящимся на единицу длины, перпендикулярной линиям тока:

jS =di/dl (А/м).

Если теперь применить уравнения электромагнитного поля в интегральной форме к элементарному контуру и элементарной призме то, учитывая, что в проводнике электромагнитное поле отсутствует, можно получить следующие гра-

	ничные условия на поверхности проводника: Et = 0; E n =	σ S	; Нn = 0; H t	= j S′ ,
		ε 0

где j S′ − проекция вектора плотности поверхностного тока на направление N,

определяемое ортом N 0 =[n 0 ,t 0 ], n 0 , t 0 − единичные векторы нормали и ка-

сательной.

Итак, касательные (тангенциальные) составляющие векторов электрического поля равны нулю на стенках волновода. Это значит, что E xm = 0 при у = 0

и y = b (см. рис. 10.5); E ym = 0 при х = 0 и х = а; E zm = 0 при х = у = 0, х = а и y

= b.

15

Из уравнения (10.25) следует, что векторный потенциал должен удовлетворять тем же требованиям (т.е. ГУ), что и E zm .

Обращаясь к уравнению (10.17): A zm = Dsin( ξx + ψ x )sin( ηy + ψ y )e − jαz ,

получаем следующее:

а) из условия A zm = 0 при х = 0 и х = а вытекает, что sin( ξx +ψ x ) = 0. То-

гда полагая х = 0, получаем sinψ x =0 и значит ψ x = 0 . Если же положить х = а,

	то получаем sin ξa = 0 , откуда ξa = mπ и	ξ =	mπ	,							(10.26)
			a
	где m − целое число;
	б) из условия A zm = 0 при у = 0 и y = b			следует, что sin( ηy +ψ y							) = 0 и
							и
	действуя аналогично предыдущему пункту, получим				ψ y	= 0		η=	nπ	,	(10.27)
									b

где n − целое число.

Подставляя найденные значения четырех постоянных в уравнение (10.17) для векторного потенциала, получаем

A zm	= Dsin	mπ x sin		nπ y e − jαz .	(10.28)
		a		b

Подставляя (10.28) в (10.20)…(10.25) получаем значения составляющих

поля:

∂ A zm

nπ

mπ

nπ

− jαz

H xm

=

=

Dsin

x sin

y e

;

(10.29)

∂y

b

a

b

∂ A zm

mπ

mπ

nπ

− jαz

H ym

= −

= −

Dsin

x sin

y e

;

(10.30)

∂x

a

a

b

E xm

=

α

H ym ;

(10.31)

ωε 0

E ym

=

α

H xm ;

(10.32)

ωε

0

E zm

= k 2

− α 2

A zm ,

(10.33)

jωε 0

16

Найденные значения постоянных удовлетворяют всем «нулевым» граничным условиям Et = 0 и Нn = 0. «Ненулевое» граничное условие, напримерH t = ± j S′ можно использовать для нахождения постоянной интегрирования

D , но это, очевидно, связано с конкретными условиями возбуждения волновода, качественно не влияющими на структуру излучаемых полей. Поэтому оставим указанную постоянную неопределенной или примем её равной 1. Эта постоянная может быть найдена исходя из конкретной мощности, пропускаемой волноводом.

Последняя постоянная α зависит от значений

ξ =

mπ

и

η=

nπ

согласно

b

a

2

2

2

2

2

4 π2

2

m 2

n 2

(10.16) как α = k

− (ξ

+ η

) или α =

2

−π

2

+

2

(10.34)

λ

a

b

.

Перейдем к анализу полученных результатов расчета.

Постоянная α играет роль коэффициента распространения для всех решений. Действительная α определяет фазу волны в волноводе ωt − αz . Отсюда фа-

зовая скорость волны в волноводе

dz

ω

ω k

k

k

v =

=

=

= c

> c , т.к.

>1

(10.35)

dt

α

k α

α

α

и длина волны в волноводе

2 π

2

π k

k

k

Λ =

=

k

= λ

> λ, т.к.

>1

.

(10.36)

α

α

α

α

Если α мнимая величина, то значит волна вдоль волновода не распространяется, а электромагнитное поле, меняясь гармонически в каждой точке, затухает экспоненциально вдоль волновода без переноса энергии. Это подтверждается наличием сдвига фаз на 900 между поперечными составляющими векторов Е и Н и, соответственно, мнимой величиной продольной составляющей вектора Пойнтинга.

Итак, для существования волны в волноводе (т.е. передачи энергии или сигнала в нем) необходимо, чтобы α 2 > 0 и, значит, чтобы волна в волноводе

17

была меньше, чем некоторое значение, названное критической длиной волны λ кр , т.е. чтобы

λ<		2	=λкр.	(10.37)
	m 2		n 2
		+
	a	b

Из (10.37) видно, что λ кр зависит от размеров поперечного сечения волно-

вода и от значений целых чисел m и n , которые могут начинаться для волн типа Е или ТМ только с единицы, так как при m = 0 или n = 0 обращаются в нуль и векторный потенциал и все связанные с ним величины в уравнениях (10.28) … … (10.33). Наибольшее значение λ кр получается при m = n= 1. Она равна

λкр11 =			2	,
	1	2	1	2
			+
	a		b

где индексы 11 указывают значения m и n, соответственно. Коэффициент распространения можно выразить через λ кр :

4 π2

λ2 m 2

n 2

2 π

λ2 m 2

n 2

2 π

λ

2

α=

1−

+

=

1−

+

=

.(10.38)

λ2

4

b 2

λ

4

b 2

λ

1−

λкр

a

2

a 2

Длина волны в таком волноводе

Λ = 2 π =

λ

> λ,

(10.39)

α

λ

2

1 −

λ кр

или

Λ =

2 π

k

= λ

k

,

(10.40)

k

α

α

а фазовая скорость волны

v = Λf

=

λf

=

c

> c ,

(10.41)

2

2

λ

λ

1 −

1 −

λ кр

λ кр

или

v = Λf

= λ

k

f

= c

k

.

(10.42)

α

α

18

Если числа m и n (или оба сразу) принимают значения больше единицы, то критическая длина волны уменьшается согласно (10.37). Может оказаться, что эта меньшая длина волныλ кр всё ещё превышает длину волны λ источника (ге-

нератора) сигнала, тогда в волноводе возможна наряду с прежней новая волна большей длины и большей фазовой скорости. В соответствии с этим к обозначению типа волны принято добавлять индексы m n (например, волна типа Е m n). Смысл чисел m и n следует из рассмотрения структуру поля в поперечных плоскостях, в которых образуются стоячие волны. Из этого следует, что число m определяет число стоячих полуволн в направлении оси х, а число n − число полуволн вдоль оси у. На рис. 10.6 приведены структуры поля волн Е11 и Е12.

В заключение отметим, что согласно ГУ H t = ± j S′ и ε 0 E n = σS уравне-

ния (10.29)….(10.32) позволяют найти распределение комплексных амплитуд поверхностных токов и зарядов на соответствующих стенках волновода. Для волн типа ТМ поверхностные токи проводимости проходят параллельно оси волновода и, меняясь от точки к точке, дополняются токами смещения, пропорциональными нормальной к плоскости стенки волновода составляющей вектора E m .

а)

б)

Рисунок 10.6 − Структуры полей волн Е11 (а) и Е12 (б)

В другом варианте решения задачи для прямоугольного волновода получатся поперечные электрические волны (ТЕ или Н волны). Такие волны удобно описывать электрическим векторным потенциалом Fm − оператором, формально

19

вводимым для полей при выполнении равенства div E m = 0 (по аналогии с век-

торным магнитным потенциалом) выражением E m =rot Fm . По аналогии с маг-

нитным векторным потенциалом относительно вектора Н электрический векторный потенциал Fm ортогонален направлению вектора Е и удовлетворяет волновому уравнению.

Решение волнового уравнения для F zm имеет вид
			F zm		= Dsin( ξx + ψ x )sin( ηy + ψ y		)e − jαz ,				(10.43)
где по-прежнему α 2 − k 2 + (ξ 2 + η 2 ) = 0.
Напряженность электрического поля определится из уравнения
						E m = rot F m ,
откуда
E xm	=	∂ F zm		= ηDsin( ξx + ψ x )cos( ηy + ψ y )e				− jαz	;		(10.44)
			∂y
E ym	= −		∂ F zm			= −ξ D cos( ξx + ψ x )sin( ηy	+ ψ y )e		− jαz	;	(10.45)
			∂x
E zm	= 0 .										(10.46)

Постоянные (кроме D) найдем из ГУ E t = 0.

В рассматриваемом случае составляющая E xm = 0 при у = 0 и у = b. Из

(10.44) видно. Что при этих значениях у должно обращаться в нуль выражение

cos( ηy +ψ y ) . Следовательно,

ψ y

= π

; η=

nπ

.

2

b

Составляющая E ym = 0 при х = 0 и х = а, т.е. при этих значениях х должен

равняться нулю и cos( ξx +ψ x

) , а, значит: ψ x =

π;

ξ =

mπ

.

2

a

Таким образом, окончательное решение для векторного потенциала F zm и

для составляющих вектора E m принимают вид:

mπ

nπ

− jαz

;

(10.47)

F zm = D cos

x cos

b

y e

a

20