Моделирование транспортных процессов и систем
.docx|
АННОТАЦИЯ
При изучении данной дисциплины ДС.02 «Моделирование транспортных процессов и систем» выполняется курсовой проект. «Формирование системы оптимальных грузопотоков», который является завершающим этапом изучения дисциплины. Целью курсового проекта являются закрепление, систематизация и углубление полученных знаний; приобретение навыков системного проектирования прогрессивных перевозочных технологий; умение пользоваться нормативно-справочной литературой.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ 2 Задание 2 1.Роль математических методов в принятии эффективных управленческих решений при автомобильных перевозках Виды моделей и эвристические методы решения задач 2 2.Понятие корреляционно-регрессионный анализ 2 3. Модели линейного программирования в решении задач автомобильных перевозок основные понятия, графоаналитический и симплексный методы 2 4. Маршрутизация перевозок помашинными отправками основные этапы решения задач 2 6. Методы планирования перевозок по сборно - развозочным маршрутам 2 7. Понятие о теории массового обслуживания в решении задач автомобильных перевозок 2 Задача № 1 2 ЗАДАЧА № 2 2 ВЫВОД 2 БИБЛИОГРАФИЧЕСКИЙ СПИСОК 2
ВВЕДЕНИЕ Транспортная система – это совокупность реальных объектов и связей между ними, которые используются на определенной территории для выполнения перевозок. Автомобильно-дорожный комплекс России (АДК) включает в себя: автотранспортные предприятия и транспортные средства; автомобильные дороги и организации, поддерживающие их в рабочем состоянии; организации, обеспечивающие ремонт и техническое обслуживание автотранспортных средств; организацию и систему контроля транспортными потоками на дорожной сети; места стыковки автомобилей с другими видами транспорта. АДК России имеет все признаки большой сложной, динамической системы, так как включает наличие большого числа взаимодействующих подсистем и элементов, имеет иерархический характер построения (подчиненности), множественность функций, наличие управления, взаимодействие с окружающей средой и воздействие случайных факторов, большую размерность задач. По мощности осваиваемых пассажиро- и грузопотоков отдельные транспортные подсистемы АДК принято подразделять на 7 групп (систем). 1. Микросистемы (маятниковые маршруты с одним автомобилем и обратным холостым пробегом). 2. Особо малые системы (кольцевые и маятниковые маршруты с одним автомобилем) различных типов с несколькими работающими транспортными средствами. 3. Малые системы – кольцевые и маятниковые маршруты различных типов с несколькими работающими транспортными средствами. Сюда относятся небольшие транспортные фирмы и транспортные отделы фирм малого бизнеса. 4. Средние системы – совокупность нескольких малых систем. Сюда относятся, например, железобетонные заводы, контейнерные станции, базы снабжения вместе с транспортными средствами и получателями товаров. 5. Большие системы – сюда относятся автомобильные парки и грузовые АТП с подвижным составом и их маршрутами. 6. Особо большие системы - автотранспортные тресты, производственные управления и объединения. 7. Суперсистема включает множество вышеуказанных систем, например Департамент автомобильного транспорта России. Автомобильные и транспортные процессы в вышеуказанных системах включают большое количество задач по управлению АДК, разработке технологических схем организации перевозок, формированию систем оптимальных грузопотоков, маршрутизации перевозок, формированию сменно-суточных планов, выбору кратчайших путей движения, закреплению потребителей за поставщиками, транспортные задачи с запретами и по критерию времени и так далее.
Задание 1. Роль математических методов в принятии эффективных управленческих решений при автомобильных перевозках. Виды моделей и эвристические методы решения задач. 2. Понятие корреляционно-регрессионный анализ. 3. Модели линейного программирования в решении задач автомобильных перевозок – основные понятия, графоаналитический и симплексный методы. 4. Маршрутизация перевозок помашинными отправками – основные этапы решения задач. 5. Методы определения кратчайших расстояний перевозок. 6. Методы планирования перевозок по сборно - развозочным маршрутам. 7. Понятие о теории массового обслуживания в решении задач автомо- бильных перевозок. Задача №1 Имеются i=4 пункта отправления груза А1, А2, А3, А4 и j=6 пунктов назначения груза В1, В2, В3, В4, В5, В6. Обозначим ресурсы груза в i-м пункте отправления через аi , i =1, 2, 3, 4, а потребность каждого j-го пункта потребления через bj, j = 1, 2, 3, 4, 6. Заданы расстояния между пунктами отправления и пунктами назначения (табл. 1). Требуется составить такой план xij перевозок грузов, который обеспечит удовлетворение запросов всех потребителей груза при минимальной транспортной работе (минимальной сумме тонно-километров). Задача является задачей линейного программирования, при решении рекомендуется использовать метод потенциалов. Исходные данные для решения задачи (объемы отправления аi и потребления bj груза) выбираются из табл. 2 в соответствии с шифром студента.
Таблица 1 Расстояния между пунктами, км
Таблица 2 Объемы перевозок груза, т
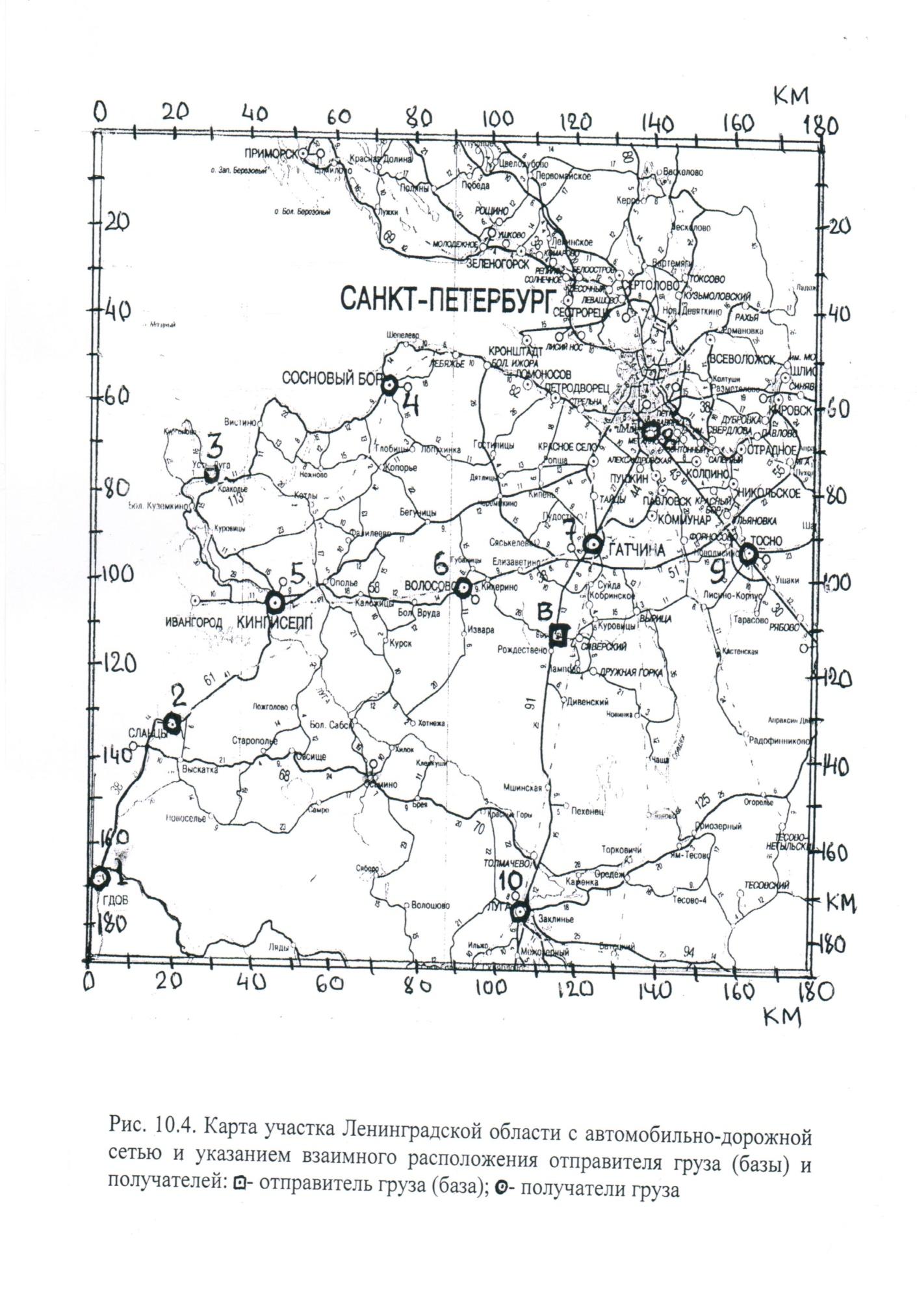
Задача №2 Составить граф (схему) транспортной сети участка Ленинградской области, показанного на рис. 1. Граф представить на чертеже А1. При составлении графа учесть основные (главные) дороги, показанные на рис. 1 толстыми линиями. Вершинами графа являются отправитель (В) и получатели (1…10) груза, основные населенные пункты, перекрестки. Расстояния между вершинами (длины звеньев графа) определить по указанному на рис. 1 масштабу и указать длины на звеньях графа в км. Участки между вершинами графа соединять прямыми линиями (звеньями). Выполнить проектирование развозочного маршрута с пунктом погрузки в точке В и 3 пунктами разгрузки (рис. 1). Точки разгрузки и их потребность в грузе выбираются по предпоследней цифре шифра студента по табл. 3.
Рис. 1. Карта участка Ленинградской области с автомобильно-дорожной сетью и указанием взаимного расположения отправителя груза (базы) и получателей: - отправитель груза (база); - получатель груза



Критерием выбора маршрута является минимальное расстояние перевозок с учетом величин транспортной работы в т·км.
Таблица 3
Пункты разгрузки груза и их потребность в грузе для составления развозочного маршрута
Значительная часть внутренних грузовых перевозок в России выполняется автомобильным транспортом, и эта часть постоянно растет. В этом Россия следует за нашим соседом Евросоюзом, где автомобильные перевозки составляют уже более 80% всего внутреннего грузооборота. Эффективным способом снижения транспортных затрат является использование новых технологий при организации автомобильных перевозок. К таким новым технологиям относится математическое моделирование, позволяющее существенно повышать качество планирования, маршрутизации и управления подвижным составом и снижать себестоимость перевозок на десятки процентов. Это в первую очередь относится к перевозкам массовых грузов (помашинным и мелкопартийным перевозкам), осуществляемым многими тысячами отечественных автотранспортных фирм. Особо в технологии математического моделирования следует отметить бурно развивающийся в настоящее время раздел «Теория массового обслуживания». Разрабатываемые в этом разделе методы позволят прогнозировать будущее поведение автотранспортной системы еще на стадии проектирования, наиболее оптимально распределять производственные ресурсы транспортной фирмы, избегать кризисных явлений, стабильно осуществлять перевозки грузов по системе «точно-вовремя». Базой развития этих методов являются новые спутниковые технологии позиционирования и определения в глобальном пространстве данных по элементам перевозочного процесса, технологии быстрой передачи этих данных на центральные компьютеры транспортных и экспедиторских фирм и их высокоскоростной обработки с учетом вероятностных характеристик транспортных процессов. Для специалиста, занимающегося автомобильными перевозками, владение методами математического моделирования во многом определяет уровень его квалификации и карьерный рост. Для транспортной фирмы использование в производстве технологий математического моделирования повышает ее конкурентоспособность и финансовую устойчивость на рынке. Для городов и регионов России оптимизация автомобильных перевозок дает заметный социальный эффект, так как ведет к снижению загрязнения атмосферы вредными выбросами от автомобилей и улучшает экологическую обстановку в целом. Для решений транспортных задач разрабатываются новые методики, базирующиеся на использовании новых технологий и методов расчета. К таким новым технологиям относятся моделирование и использование моделей для решения задач управления и принятия решений. Во многих ситуациях они являются единст
венно возможным и эффективным методом, позволяющим получить ответ на поставленный вопрос. Модель - это аналог, макет или иной вид отражения наиболее важных черт, свойств и результатов транспортных систем и процессов. Адекватность модели - это свойство модели быть основой для прогнозирования событий, протекающих в транспортных системах и процессах, и давать подтверждаемые результаты. Моделирование – это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели. Теория моделирования – это теория замещения одних объектов-оригиналов другими объектами (моделями) и исследования свойств объектов на их моделях. В зависимости от характера изучаемых процессов в системе все виды моделирования могут быть разделены на детерминированные и стохастические; статические и динамические; дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование отображает детерминированные процессы, то есть процессы, в которых предполагается отсутствие всяких случайных воздействий. Стохастическое моделирование отражает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики. Статическое моделирование служит для описания поведения объекта в какой-либо момент времени, а динамическое моделирование отражает поведение объекта во времени. Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, а непрерывное отражает непрерывные процессы в системах. В зависимости от формы представления объекта (системы) можно выделить мысленное и наглядное моделирование. При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте (механические, графические и другие). При исследовании транспортных процессов и систем на автомобильном транспорте наиболее широко используется математическое моделирование, являющееся разделом мысленного моделирования. Под математическим моделированием понимают установление соответствия данному реальному транспортному процессу или системе некоторого математического объекта, называемого математической моделью и исследование этой модели, позволяющее получить характеристики рассматриваемого реального транспортного процесса и транспортной системы. Любая математическая модель, как и всякая другая описывает реальную систему и процесс лишь с некоторой степенью приближения к действительности.
При решении практических задач автомобильно-дорожного комплекса, как правило, не применяются строгие методы решений. Широко используются смекалка и интуиция инженерно-технического и управленческого персонала. В модели реальных транспортных процессов и систем вносятся упрощающие допущения. Такой метод позволяет подобрать для решаемой задачи из набора средств современной математики приемлемый алгоритм и найти хотя бы приближенное решение. Такие методы решений задач в условиях, когда нельзя точно определить границы их применения и оценить допустимые погрешности, называются эвристическими. Преимущества математического моделирования перед другими видами (графическим, аналоговым, механическим и т.д.) заключаются в широком использовании математических моделей, низкой стоимости их создания, быстром получении результатов исследований, возможности проведения расчетных экспериментов и проверки правильности построения модели. Конечно, математическая модель всегда является упрощенной, однако она является достаточно наглядной и позволяет адекватно описать транспортную систему и транспортный процесс. Математическое моделирование при решении задач АДК можно разделить на оптимизационное (аналитическое) и имитационное. Соответственно математические модели можно разделить на аналитические и имитационные.
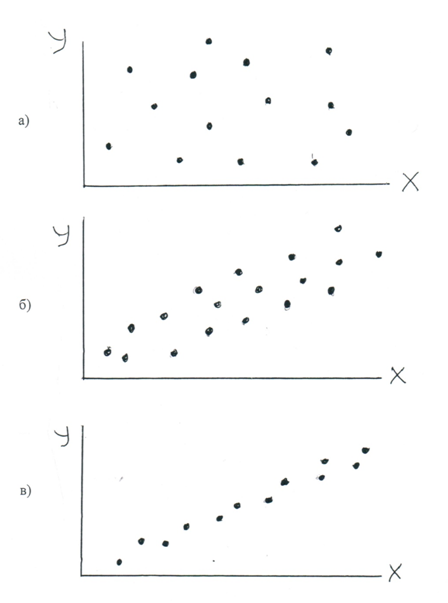
Корреляция в переводе с латинского обозначает соответствие или взаимосвязь. Корреляционная зависимость отражает связь между величинами, когда определенным значениям факториальных величин соответствует много значений зависимой величины. Корреляционный анализ в задачах моделирования транспортных процессов и систем имеет фундаментальное значение, так как теснота корреляционной связи определяет структуру модели. Высокая и полная корреляционная связь требует объединения величин. Отсутствие или слабость корреляционных связей позволяют рассматривать величину как независимую. Во многих случаях выбор независимых величин на базе исследования их корреляционных связей требует дополнительного экспертного исследования и решения. Корреляционная связь между двумя переменными изучается с помощью парной корреляции. О тесноте корреляционной связи можно судить по характеру расположения точек на графике, связующем переменные х и у. Такой график называется полем корреляции (рис. 2). Разброс точек по всему полю свидетельствует об отсутствии корреляции (рис. 2,а), рис. 2,б свидетельствует о слабой умеренной корреляции, рис. 2,в - о полной корреляции.
Рис. 2. Расположение точек на корреляционном поле: а) корреляционная связь отсутствует; б) слабая и умеренная корреляционная связь; в) полная корреляционная связь
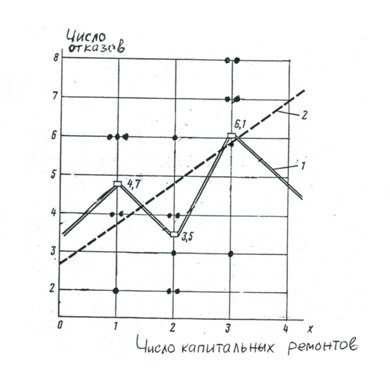
Численное значение корреляционной связи оценивается коэффициентом корреляции r. Задачей регрессионного анализа является установление вида зависимости (1.2) (зависимости параметра оптимизации у от факториальных величин х1, х2…хn). Указанная зависимость называется уравнением регрессии. Корреляционно-регрессионный анализ позволяет прогнозировать развитие рассматриваемого явления и решать задачу построения модели и ее оптимизации. Регрессионный анализ введен в практику расчетов английским математиком и механиком У.Р. Гамильтоном в 1840-х годах. При проведении регрессионного анализа применяются понятия парных и множественных коэффициентов регрессии. На рис. 2 показано корреляционное поле парной линейной зависимости, отказов автомобилей в эксплуатации от числа капитальных ремонтов. Рассмотрение расположения точек на поле рис. 2 позволяет говорить о слабой корреляционной зависимости, разброс точек на рис. 2 примерно соответствует рис. 1,б. Из рис. 3 видно, что если для каждой величины х найти средние значения у и соединить эти точки, то получится ломанная линия, называемая опытной линией регрессии.
Рис. 3. Регрессионная зависимость числа отказов автомобилей в эксплуатации от числа капитальных ремонтов: 1-опытная; 2-теоритическая; •-точки опытных данных; □-средние арифметические числа отказов автомобилей по каждой группе
При парной зависимости опытная линия регрессии может быть аппроксимирована с помощью следующих функций: у = а + b х – прямая линия; у = а х2 + b х + с – парабола второго порядка;
у =
у = а + b lg х – логарифмическая функция. Используются также показательная и степенная функции, арифметическая и геометрическая прогрессии, алгебраический полином, тригонометрический ряд (ряд Фурье) и другие функции. В общем случае для n переменных уравнение регрессии приобретает более сложный вид.
3. Модели линейного программирования в решении задач автомобильных перевозок основные понятия, графоаналитический и симплексный методы Линейное программирование – это наиболее разработанный раздел математического программирования, с помощью которого выполняются анализ и решение экстремальных задач с линейными связями и ограничениями. Линейное программирование включает в себя целый ряд эвристических (приближенных) методов решения, позволяющих при заданных условиях из всех возможных вариантов решений производственных задач выбрать наилучший, оптимальный. К этим методам относятся следующие – графический, симплексный, метод потенциалов (модифицированный распределительный метод – МОДИ), Хичкова, Креко, метод аппроксимации Фогеля и другие. Часть этих методов объединяют общим названием - распределительный, или транспортный, метод. На автомобильном транспорте методы линейного программирования используются с 1960-х годов для решения большого числа важнейших производственных задач, а именно: сокращение дальности перевозок грузов; составление оптимальной схемы перевозок; выбор кратчайших маршрутов движения; задачи перевозки разных, но взаимозаменяемых грузов; сменно-суточное планирование; планирование перевозок мелкопартионных грузов; распределение автобусов по маршрутам и другие. Особенности модели линейного программирования заключаются в следующем: - целевая функция и ограничения выражены линейными зависимостями (равенствами или неравенствами); - число зависимостей всегда меньше числа неизвестных (условие неопределенности); -неотрицательность искомых переменных. Общая форма записи модели линейного программирования в сокращенном виде выглядит следующим образом: - найти хij ≥ 0 (j = 1, 2…n) при ограничениях следующего типа:
Эти ограничения минимизируют (или максимизируют) целевую функцию
Графоаналитический метод – это один из простейших методов линейного программирования. Он наглядно раскрывает сущность линейного программирования, его геометрическую интерпретацию. Его недостаток в том, что он позволяет решать задачи с 2 или 3 неизвестными, т. е. применим для узкого круга задач. Метод основан на правилах аналитической геометрии.
Решение задачи с двумя переменными х1 и х2, которые по смыслу задачи не должны быть отрицательными, выполняется в системе декартовых координат. Уравнения х1=0 и х2 = 0 являются осями системы координат первого квадранта (рис. 4).
Рис. 4. Графический метод решения задачи по перевозке изделий из пенобетона и стали на максимум прибыли
Симплексный метод – это распространенный метод решения задач линейного программирования. Свое название метод получил от слова «симплекс», обозначающего простейший выпуклый многоугольник, число вершин которого всегда на единицу больше, чем размерность пространства. Симплексный метод разработан в США математиком Дж. Данцигом в конце 1940-х годов. Симплексный метод включает получение неотрицательного базисного решения системы канонических линейных уравнений, последующую минимизацию (максимизацию) целевой функции и нахождение таким способом оптимальных значений искомых переменных х1, х2… хn. Идея симплексного метода заключается в том, что в процессе вычисления последовательно переходят от первого базисного решения ко второму, третьему и т.д. с помощью так называемых симплексных преобразований. Преобразования производятся в форме симплексных таблиц, что значительно упрощает и ускоряет расчеты. Чтобы получить неотрицательные базисные решения системы линейных уравнений, надо процесс исключения неизвестных вести так, чтобы свободные члены уравнений на всех этапах процесса оставались неотрицательными. При этом следует руководствоваться следующим правилом: в качестве новой базисной переменной принимается любая свободная
переменная, при которой есть хотя бы один положительный коэффициент; выводится из базиса переменная, которая соответствует наименьшему отношению свободных членов уравнений к соответствующим положительным коэффициентам уравнений при вводимой в базис переменной. Такие преобразования называются симплексными преобразователями. Это очень важно, поскольку для нахождения частного неотрицательного решения, отвечающего наибольшему возможному значению какой-то одной свободной переменной при нулевых значениях других свободных переменных, вместо определения области изменения указанной переменной и подстановки ее наибольшего возможного значения в общее решение достаточно принять эту переменную за базисную и подвергнуть систему симплексному преобразованию, перейдя к новому базису, что значительно упрощает расчеты. Вычисления удобно производить с помощью симплексных таблиц. Переход от одной таблицы к другой соответствует одной итерации, т. е. переходу от одного базиса к другому, при этом значение целевой функции уменьшается. За определенное число итераций переходят к базису, для которого получают оптимальное (минимальное или максимальное) значение целевой функции. Рассмотрим симплексный метод в общем виде. Общая задача линейного программирования заключается в минимизации (максимизации) целевой функции, переменные которой связаны между собой системой линейных уравнений, подчинены условию неотрицательности. Основные правила симплексного метода линейного программирования (при решении задачи на минимум): 1) систему ограничений задачи линейного программирования необходимо решить относительно какого-либо базиса. Выразить целевую функцию через свободные переменные; 2) составить симплексную таблицу. Если в индексной строке все элементы отрицательны, то базисное решение оптимально. Задача решена; 3) если в индексной строке симплекс-таблицы есть положительные элементы, то столбец, соответствующий минимальному из них, принимается за разрешающий. Составляются отношения элементов столбца свободных членов к положительным элементам разрешающего столбца. Строка, соответствующая минимальному из этих отношений, является разрешающей. Элемент таблицы, находящийся на пересечении разрешающего столбца и разрешающей строки, называется разрешающим; 4) переходить к новому базису следует, исключая из старого базиса переменную, соответствующую разрешающей строке, вводя вместо нее переменную, которая соответствует разрешающему столбцу. Составляется новая симплекс-таблица, соответствующая новому базису.
4. Маршрутизация перевозок помашинными отправками основные этапы решения задач При помашинных отправках грузов каждый отдельный автомобиль загружается только в адрес одного потребителя. Сменно-суточное планирование таких перевозок занимает одно из центральных мест в задачах маршрутизации и включает составление маршрутов движения подвижного состава и порядок его следования между корреспондирующими точками. Оптимальное планирование рассматриваемой задачи позволяет получать значительный экономический эффект. Первым шагом работы по составлению рациональных маршрутов является классификация грузов, предъявляемых к перевозке, на группы, однородные с точки зрения возможности их перевозки на одном и том же подвижном составе. Маршруты составляются по каждой группе грузов. Практика решения задач по маршрутизации перевозок грузов учитывает множество ограничений, вызываемых конкретными условиями работы грузовых точек и автомобильного транспорта. К ним относятся: заданное множество пунктов отправления и получения грузов; объемы грузооборота у поставщиков и потребителей; характер груза, время доставки, структура и наличие парка подвижного состава; мощность и размещение автотранспортных предприятий; режимы работы водителей и так далее. Многообразие ограничений в каждом конкретном случае привело к созданию различных методов маршрутизации, в том числе и эвристических, базирующихся на материалах опыта прошлой работы. Имеется большое число методов маршрутизации массовых грузов, когда грузы перевозятся помашинными отправками, используются сложные алгоритмы решения задач. В настоящем разделе рассмотрен один широко используемый метод маршрутизации – метод совмещенных планов. Метод используется на базе линейного программирования. Основной задачей сменно-суточного планирования является составление такого плана работы транспортных средств на данную смену, который позволит выполнить заданные перевозки в установленные сроки минимальным количеством автомобилей. Достигается это при максимальной производительности подвижного состава, которая в общем виде выражается формулой:
где Р – производительность автомобиля за смену, т·км; Тн – время в наряде, ч; g –грузоподъемность автомобиля, т; γ – коэффициент использования грузоподъемности; β – коэффициент использования пробега; Vт – техническая скорость, км/ч; lг – расстояние перевозки груза, км; tпр –простой автомобиля при погрузке и выгрузке, ч. Воздействуя на указанные технико-эксплуатационные показатели, можно увеличить производительность подвижного состава.
Из всех вышеуказанных факторов от качества сменно-суточного планирования на автотранспортном предприятии в наибольшей степени зависит коэффициент использования пробега. Таким образом, задача ежедневного планирования перевозок грузов на автотранспортном предприятии формируется как задача обеспечения заданного объема перевозок грузов с наименьшим порожним пробегом автомобиля. Эта задача маршрутизации состоит в следующем. Разнородный груз сосредоточен в пунктах отправления А1, А2…Аi…Аm в количествах соответственно а1, a2…ai…am единиц. Его необходимо доставить в пункты назначения В1, В2…Вj…Вn в количествах в1, в2…вj…вn соответственно. Объём перевозок из i-го пункта отправления в j-й пункт назначения составляет qij единиц и известен для всех пунктов. Расстояние от i-го пункта отправления до j-го пункта назначения равно lij и известно для всех комбинаций ij. В процессе выполнения перевозок в пунктах назначения В1, В2…Вj…Вn после разгрузки автомобилей будет образовываться порожняк в количествах в11, в21…вj1…вn1 единиц. Этот порожняк необходимо подать под очередную загрузку в пункты отправления А1, А2…Аi…Аm в количестве а11, а21…аi1…аm1. Величины аi, вj, qij, ai1, вj1 могут выражаться либо в тоннах, либо в ездках автомобиля. Для существа задачи это безразлично, тем более что тонны всегда можно перевести в ездки. Однако с методической точки зрения удобнее пользоваться ездкой автомобиля с грузом и без груза. Количество прибывающих в пункт назначения гружёных автомобилей представляет ресурсы порожняка в данном пункте. Количество убывающих из пункта отправления гружёных автомобилей – потребность этого пункта в порожняке. По смыслу рассматриваемой задачи всегда имеет место условие:
вj1
= вj=
ai1
= ai
=
Расстояние от Вj до Аi, равное lji=lji, известно для всех сочетаний i, j. За смену каждый автомобиль выполняет несколько ездок с грузом из одного или нескольких пунктов отправления в один или несколько пунктов назначения. После каждой ездки с грузом автомобиль возвращается в пункт отправления порожняком. Из каждого пункта назначения автомобиль может следовать под погрузку в любой пункт отправления, имеющий груз.
Дополнительным условием задачи является требование, чтобы за рабочую смену автомобиль направлялся не более чем в 4 разных пункта отправления и такое же количество пунктов назначения. Практически это означает, что при сменном задании с большим числом ездок необходимо составлять кольцевой маршрут так, чтобы по нему можно было сделать несколько оборотов. Таким образом, требуется составить такой план перевозок (маршруты движения автомобилей и сменные задания водителям), который обеспечит выполнение заданных объёмов перевозок с наименьшим холостым пробегом автомобилей.
5. Методы определения кратчайших расстояний перевозок Табличный метод: Если два пункта находятся в пределах видимости, то кратчайший путь между ними можно выбрать, не применяя никаких вычислений. Когда пункты достаточно удалены друг от друга, то возникают различные варианты передвижения, которые необходимо сравнивать, чтобы выбрать наилучший. На рис. 5 представлена модель участка транспортной сети, сформированная на основе карты экономического региона. Задача о нахождении кратчайшего пути между пунктами (рис. 5) может быть в общем виде сформулирована на основе положений графов следующим образом. Дан граф G = (x, y). Каждому ребру графа приписано некоторое число (длина ребра) lij ≥ 0. Тогда любая цепь μ, составленная из нескольких ребер, характеризуется длиной lμ. Требуется для двух произвольных вершин найти такой путь, чтобы его длина была наименьшей:
Рис. 5. Определение кратчайших расстояний по транспортной сети методом потенциалов
Пусть задана транспортная сеть, состоящая из пунктов А1, А2…, Аi…, Аm и дорог, соединяющих эти пункты между собой. Длины участков дороги между каждой парой соседних пунктов Аi Аj известны и равны ljj. Если два соседних пункта Аi и Аj непосредственно не соединены между собой участком дороги, то принимаем ljj= ∞. Из начального пункта А1 в
конечный пункт Аm можно попасть по большому числу маршрутов, проходящих через разные промежуточные пункты. Требуется найти среди этих маршрутов путь наименьшей протяженности. Переведём задачу на формальный язык. Обозначим каждый участок сети между двумя соседними пунктами Аi и Аj числом xij= 1, если он является звеном выбранного маршрута движения из Аi в Аm, и xij=0, если он не входит в этот маршрут. Тогда задача отыскания кратчайшего пути из Аi в Аm сводится к выбору чисел xij (i, j = 1, 2, …, m), при которых достигает минимума линейная форма
при условии
xij ≤1, i, j =1,2………….m (6.7)
Линейная форма (6.3) определяет длину маршрута между начальным и конечным пунктами. Условия (6.4) означают, что для любого 0≤пункта маршрута Аi, исключая начальный и конечный, число дорог, входящих в этот пункт, равно числу дорог, выходящих из него. Поскольку lji>0 для всех I и j, условия (6.4) вместе с требованием минимизации линейной формы (6.3) означают, что из каждого пункта Аi (i=2, 3, …, m -1) выходит не более одной дороги. Условия (6.5) фиксируют тот факт, что количество дорог, выходящих из начального пункта маршрута, Аi превышает на единицу число дорог, входящих в этот пункт. Аналогично условия (6.6) указывает на то, что в последний пункт Аm входит на одну дорогу больше, чем выходит. Условия (6.5) и (6.6) вместе с условиями (6.4) и требованием минимизации линейной формы (6.3) означают, что в каждый пункт маршрута входит ровно одна дорога и из каждого пункта маршрута исходит ровно одна дорога. Наконец, условия (6.7) требуют, чтобы все xij были равны нулю или единице. В целом, соотношения (6.3-6.7) представляют собой определение кратчайшего пути на сети дорог между двумя заданными пунктами, т.е. аналитическую модель рассматриваемой задачи. Параметры lji при необходимости могут означать не только расстояния, но и продолжительности проезда по участкам сети или стоимость пробега автомобиля. Поскольку условия задачи записаны в виде линейных уравнений и неравенства, а критерий показателя качества решения выражается линейно, сформулированная задача является задачей линейного программирования. Рассмотрим процесс решения этой задачи с помощью метода потенциалов.
Общая вычислительная схема применительно к данной задаче следующая. В специальную таблицу (табл. 4) типа «шахматной» Таблица 4 Базовая таблица. расчета расстояний между пунктами и индексов U и V
заносят расстояния lji от каждого пункта Аi ((i=1, 2, …, m ) до всех соседних с ним пунктов Аi ((i=1, 2, …, m ). После этого для каждого пункта Аi и Аj рассчитывают индексы ui и υj следующим образом. Индекс ui принимают равным нулю (ui =0). Затем по порядку, начиная с первой строки таблицы, рассматривают клетки с заполненными lji . Если для некоторой заполненной клетки (I, j) индекс ui уже известен, а υj - ещё нет, то определяют υj по формуле
υj= ui+ lji . (6.8)
Если при определении очередного υj в i-м столбце имеется более одной клетки с записанными lji и известными ui , то принимают
υj = min (ui+ lj) . (6.9)
Найденные значения υj записывают в соответствующие клетки вспомогательной строки, а также в клетки вспомогательного столбца, исходя из правила: u1= υ1, u2= υ2, … um= υm. После определения всех индексов υj и ui проверяют оптимальность данного решения, сравнивая все lji с их разностями (υj- ui). Если для всех заполненных клеток соблюдается условие
lij ≥υj- υj, (6.10)
то решение оптимально и каждое найденное число υj дает кратчайшее расстояние от пункта А1 до соответствующего пункта Аi, до соответствующего пункта Аj (i=1,2,…m). При
наличии хотя бы одной клетки с величиной lij <υj- ui решение неоптимально и вычисления необходимо продолжить. Предположим, что в клетке Аi n Аj n нарушено условие оптимальности (6.10), т.е. li njn< υ i n- ui n. В этих условиях необходимо изменить решение следующим образом. Индекс υ j n заменяют индексом υ` i n , величину которого определяют по формуле υ i n= υ i n+ li njn. На каждой итерации корректируют индексы υj у всех клеток с lij< υj- ui, после чего решение снова проверяют на оптимальность. Вычисления повторяют до тех пор, пока в таблице не будет выполнено условие оптимальности (6.10). При определении кратчайших расстояний от пункта А2 до всех остальных принимают u2=0, после чего находят все индексы и выполняют все описанные выше вычисления. При определении кратчайших расстояний от пункта А3 до всех остальных принимают u3=0 и т.д.
6. Методы планирования перевозок по сборно - развозочным маршрутам Оптимизация мелкопартионных перевозок грузов, когда размер отправляемой или получаемой партии груза существенно меньше грузовместимости используемых автотранспортных средств, является очень важной среди задач планирования грузовых автомобильных перевозок. При этих перевозках автомобили функционируют на развозочных, сборных, развозочно-сборных (далее развозочных) маршрутах в составе комплекса различных автотранспортных систем (РСТС). Используется классификация систем по комплексу признаков (выполняемая функция, конфигурация системы, мощность грузопотоков, количество пунктов погрузки-выгрузки и подвижного состава и другие). Все РСТС делятся на 9 видов. 1. Развозочная Sp – система, состоящая из пункта погрузки, множества пунктов разгрузки, транспортных связей между ними и одного автомобиля, осуществляющего доставку груза. Технологическая схема доставки груза представляет собой развозочный маршрут. 2. Сборная Sс – система, состоящая из множества пунктов погрузки, пункта разгрузки, транспортных связей между ними и одного автомобиля, осуществляющего доставку груза. Технологическая схема доставки груза представляет собой сборный маршрут. 3. Развозочно-сборная Spc – система, представляющая собой совокупность предыдущих транспортных систем, включающая в себя множество пунктов погрузки и разгрузки, транспортных связей между ними и один автомобиль, осуществляющий доставку груза. Технологическая схема доставки груза представляет собой развозочно-сборный маршрут. 4. Простая Sп – система, состоящая из множества Sp (Sс или Spc), в которой осваиваются, по сравнению с предыдущими системами, большие грузопотоки. Примером Sп служит сбор и вывоз бытовых отходов на ассполя, сбор писем из абонентских ящиков автомобилями в отделения связи, сбор и вывоз пищеотходов, доставка по магазинам продукции бытовой химии, доставка мебели из магазинов населению и другие. 5. Развозочная с центром погрузки Sрц – система, состоящая из совокупности Sp, в которой осваиваются, по сравнению с Sp, большие грузопотоки. Пример функционирования Sрц - развоз газа в цистернах; развоз стеновых панелей с домостроительного комбината потребителям, раствора и другие. 6. Сборная с центром разгрузки Sсц – система, состоящая из совокупности Sс, в которой осваиваются, по сравнению со сборной системой, большие грузопотоки. Пример функционирования Sсц – сбор и вывоз бытовых отходов на мусороперерабатывающий (сжигающий) завод, сбор и вывоз строительного мусора по системе «несменяемых» контейнеров. 7. Комбинированная первого вида Sк1 – система, состоящая из центрального пункта с несколькими фронтами погрузки (разгрузки и погрузо-разгрузки) и множества предыду
щих транспортных систем (кроме простой системы Sп), в которой по условиям перевозок работают несколько единиц или даже десятков автомобилей. 8. Комбинированная второго вида Sк2 – система, состоящая из центрального и множества периферийных пунктов погрузки и разгрузки, транспортных связей между ними и автомобилей, осуществляющих доставку груза. Примером системы являются развоз и сбор почтовых отправлений, посылок, журналов и других почтовых грузов в отделения связи; развоз продукции в таре из хлебо- и молокозаводов и сбор возвратной тары в них; развоз мелкоштучных и контейнеропригодных грузов в контейнерах и на поддонах на строительные объекты и сбор возвратной тары. 9. Город-регион Sr-p– это система, состоящая из множества РСТС, приведенных выше, в которой по условиям перевозок работают несколько десятков и даже сотен автомобилей автотранспортного предприятия. Для грузовых перевозок можно отметить следующие: метод перебора вариантов маршрута; метод сумм; метод «ветвей и границ»; Кларка-Райта и другие. Для пассажирских перевозок - метод Б.Л. Геронимуса и другие. Необходимость учета при проектировании РСТС многочисленных требований и ограничений, часто противоречащих друг другу, особенностей функционирования реальных РСТС; выполнение значительного количества вычислительных процедур приводят к необходимости использования ЭВМ. Это обусловливает необходимость разработки обобщенного алгоритма проектирования РСТС, учитывающего особенности решения задачи проектирования для различных РСТС. Метод перебора вариантов. Число перестановок из w пунктов завоза (вывоза), включаемых в маршрут по w пунктам: Pw = w!, (8.1)
где w! – факториал целого положительного числа w, который равен произведению: w! = 1·2·3…· w. При трех пунктах груза количество возможных маршрутов М = w! = 3! = 1·2·3 = 6, таким образом, возможны шесть маршрутов доставки груза из пункта А (см. табл. 5). Выбор маршрута осуществляется по критерию «минимум затрат», чему соответствует минимум пробега. При наличии двух и более маршрутов одинаковой протяженности цели системы соответствует минимум грузооборота на маршруте.
Таблица 5 Результаты расчета пробега и грузооборота в развозочной системе
Рассмотренный пример – с числом пунктов завоза w = 3. Что будет, если потребителей 4, или 5, или 10? Согласно формуле (8.1) число вариантов маршрутов, которые необходимо будет рассмотреть, обсчитать и т.д., будет равно соответственно 24; 120; 3628800. Решение задачи с числом пунктов завоза более четырех рассмотренным способом в оперативном режиме нерационально. Проектирование маршрутов методом сумм Метод сумм является одним из наиболее простых приближенных методов решения задачи рационального объезда точек на маршруте (эта задача еще называется задачей коммивояжера). Все пункты называются вершинами сети, а линия, соединяющая две соседних вершины, - звеном. Незамкнутая сеть, связывающая две и более вершины с минимальной суммарной длиной всех соединяющих их звеньев, называется кратчайшей связывающей сетью. На транспортной сети находят наименьшее звено. Затем рассматривают все звенья, связанные с одной из своих вершин с выбранным звеном. При этом нельзя выбирать звено, соединяющее две ранее включенные в сеть вершины. Далее опять рассматривают все звенья, связанные с вершинами полученной сети, и из них выбирают наименьшее и так далее до тех пор, пока не будет выбрана сеть. Далее все пункты маршрута, начиная с А, связываются такой замкнутой линией, которая соответствует кратчайшему пути объезда этих пунктов. Первоначально при использовании метода сумм строится таблица, называемая симметричной матрицей. По главной диагонали в ней расположены пункты, включаемые в маршрут. Дополнительно в этой матрице имеется итоговая строка – строка сумм. В ней проставляют сумму расстояния по каждому столбцу. Затем строят начальный маршрут из трех пунктов, имеющих максимальную сумму по своему столбцу. Принимаем маршрут. В него включают следующий пункт с максимальной суммой. Чтобы определить, между какими пунктами его следует вставить, надо поочередно включать этот пункт между каждой парой. При этом для каждой пары этих пунктов находят величину прироста пробега автомобиля на маршруте при
включении в начальный маршрут вновь выбранного пункта. Величину этого прироста ∆кр находят по формуле
∆кр = L13 + L23 – L12, (2)
где L – расстояние; 1 – первый соседний пункт; 2 – второй соседний пункт; 3 – включаемый пункт.
7. Понятие о теории массового обслуживания в решении задач автомобильных перевозок Теория массового обслуживания является одним из разделов теории вероятностей. В последние годы она получила развитие и выделилась в самостоятельный раздел математики. Основоположником теории массового обслуживания является датский ученый А.К. Эрланг. Его первая работа по этому вопросу была опубликована в 1909 году. Идеи и методы теории массового обслуживания в настоящее время получают широкое распространение на автомобильном транспорте. Используя теорию массового обслуживания, можно находить оптимальные и близкие к оптимальным решения таких практических задач, как определение числа постов погрузки, выгрузки и технического обслуживания, оптимизация процесса заправки автомобилей топливом, определение величины резерва подвижного состава, выбор количества подвижного состава, обслуживание населения автомобилями-такси и другие. Термин массовое обслуживание означает, что речь идет не о конкретном объекте, а о совокупности объектов, потребности которых требуется удовлетворить. Особенностью теории массового обслуживания является то, что она рассматривает любой процесс массового обслуживания как вероятностный. Теория массового обслуживания занимается изучением таких транспортных процессов, в которых возникают очереди на обслуживание. Причинами возникновения очередей являются случайно изменяющиеся потребности в обслуживании, вызываемые, например, неравномерным прибытием автомобилей на погрузку–выгрузку; ограниченностью мощности погрузо-разгрузочных постов; неравномерным прибытием автомобилей на заправку топливом, на станцию технического обслуживания и ограниченностью мощности постов обслуживания; прибытие такси по вызову; подход пассажиров к остановкам городского транспорта; прибытие транспортных средств к пассажирским остановкам и так далее. С помощью теории массового обслуживания решаются задачи оптимизации вышеуказанных процессов. Общая модель системы массового обслуживания состоит из обслуживаемой и обслуживающей систем. Обслуживаемая система включает совокупность источников требований и входящего потока требований. Требование – это запрос на выполнение работы (погрузки-выгрузки, заправки топливом, ремонта, посадки в транспорт для поездки и другие). Источник требований – это объект (диспетчер, водитель, пассажир, механизм и так далее), который может послать в обслуживающую систему только одно требование. Носитель требований, например водитель, автомобиль или агрегат, которому могут понадобиться услуги, запасные части, житель города, которому понадобилось свободное такси. Требования и его носитель часто отождествляются. Требования от всех источников в обслуживающую систему образуют входящий поток требований.
Обслуживающая система состоит из накопителя и механизма обслуживания. Требования поступают в накопитель, где ожидают начала обслуживания, если есть очередь, или обслуживаются сразу. Обслуживанием считается удовлетворение поступившего запроса на выполнение услуги. Механизм обслуживания состоит из нескольких обслуживающих аппаратов. Обслуживающий аппарат – это часть механизма обслуживания, способная удовлетворить только одно требование. После окончания обслуживания требования покидают систему, образуя выходящий поток требований. Для применения теории массового обслуживания нужно изучать и анализировать фактические данные. Практическая цель применения теории – это предсказание поведения системы при ее будущей работе еще до того, как система создана, то есть на стадии проектирования системы. Основной базовой величиной в теории обслуживания является поток требований на обслуживание. Для рассматриваемых автотранспортных процессов потоки в большинстве случаев принимаются стационарными (не зависящими от начала отсчета времени, а зависящими только от его продолжительности), ординарными (когда в любой момент времени поступает только одно требование) и потоками без последствий (не зависящими от количества ранее поступивших требований). Такие потоки называются простейшими. Работа погрузочно-разгрузочных постов, постов на станциях технического обслуживания, на топливо - заправочных пунктах, обслуживающих подвижной состав, относится к разомкнутым системам. В таких системах отсутствует связь между обслуженным требованием и требованиями, поступившими на обслуживание. При этом выбор наиболее эффективного варианта загрузки системы является проблематичным. Исходить из средней загруженности системы нельзя, поскольку одним из условий нормальной работы системы является выполнение на каждой фазе работы неравенства
где λ – средняя интенсивность входящего потока требований; ν – интенсивность обслуживания одним аппаратом в единицу времени; s –число обслуживающих аппаратов; p – коэффициент использования обслуживающей системы. Если коэффициент использования p будет больше единицы, то обслуживающая система не справится с обслуживанием и очередь будет неограниченно расти. В соответствии с поведением требований системы подразделяются на три группы:
2. Система с ожиданиями, например, автомобиль ожидает погрузки; 3. Смешанные системы, например, часть автомобилей уезжает с автозапра- вочной станции, если очередь на заправку велика. Теория массового обслуживания позволяет определить оптимальный характер функционирования системы массового обслуживания по характеристикам ее частей.
Задача № 1 По исходным данным составим матрицу условий (табл. 6). В правых верхних углах клеток, представляющих собой реальные маршруты перевозок, указаны расстояния между соответствующими пунктами.
Составим данный исходный план в табл. 7.
Транспортные расходы составят: z = 5 ∙ 4 + 2 ∙ 12 + 5 ∙ 7 + 3 ∙ 6 + 4 ∙ 9 + 6 ∙ 6 + 5 ∙ 7 + 9 ∙ 4 + 11 ∙ 5 = 295 Решим задачу методом потенциалов. Т.к. m+n-1= 6 + 4 – 1 = 9 и имеем 9 загруженных клеток, план ацикличный. Пусть Ui и Vj - потенциалы i-го склада и j-го магазина соответственно. Полагая потенциал U1=0, определяем остальные потенциалы из соотношения Ui+Vj=Ci,j, просматривая все занятые клетки. Получим: U1=0 V6 =C1,6 – U1= 4 U3 = C3,6 – V6 = 3
V1 = C3,1 – U3 = 6 U2 = C2,1 – V1 = 6 V2 = C2,2 – U2 = 1 V4 = C3,4 - U3 = 3 V5 = C2,5 – U2 = 0 U4 = C4,5 – V5 = 5 V3 = C4,3 – U4 = -1 Для свободных клеток определим значения оценок (разностей между прямыми и косвенными тарифами). S1,1 = С1,1 - (U1 + V1) = -1 S1,2 = С1,2 - (U1 + V2) = 7 S1,3 = С1,3 - (U1 + V3) = 12 S1,4 = С1,4 - (U1 + V4) = 3 S1,5 = С1,5 - (U1 + V5) = 9
S2,3 = С2,3 - (U2 + V3) = 6 S2,4 = С2,4 - (U2 + V4) = 1 S2,6 = С2,6 - (U2 + V6) = -2
S3,2 = С3,2 - (U3 + V2) = 6 S3,3 = С3,3 - (U3 + V3) = 5 S3,5 = С3,5 - (U3 + V5) = 7
S4,1 = С4,1 - (U4 + V1) = -3 S4,2 = С4,2 - (U4 + V2) = 6 S4,4 = С4,4 - (U4 + V4) = 5 S4,6 = С4,6 - (U4 + V6) = 0
Имеем три клетки с отрицательными оценками – (1,1), (2, 6) и (4, 1). Выбираем клетку с наименьшей оценкой (4, 1) и строим для нее цикл табл. 8.
Перемещаем по циклу груз величиной в 2 единицы, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
Целевая функция (транспортные расходы) z = 289. Значение целевой функции изменилось на 6 единиц по сравнению с предыдущим этапом. Проверим полученный план на оптимальность. Подсчитаем потенциалы. U1=0 V6 =C1,6 – U1= 4
U3 = C3,6 – V6 = 3
V1 = C3,1 – U3 = 6 V4 = C3,4 - U3 = 3 U4 = C4,1 – V1 = 2 V3 = C4,3 – U4 = 2 V5 = C4,5 – U4 = 3 U2 = C2,5 – V5 = 3 V2 = C2,2 – U2 = 4
Для свободных клеток определим значения оценок (разностей между прямыми и косвенными тарифами). S1,1 = С1,1 - (U1 + V1) = -1 S1,2 = С1,2 - (U1 + V2) = 4 S1,3 = С1,3 - (U1 + V3) = 11 S1,4 = С1,4 - (U1 + V4) = 3 S1,5 = С1,5 - (U1 + V5) = 6
S2,1 = С2,1 - (U2 + V1) = 3 S2,3 = С2,3 - (U2 + V3) = 6 S2,4 = С2,4 - (U2 + V4) = 4 S2,6 = С2,6 - (U2 + V6) = 1
S3,2 = С3,2 - (U3 + V2) = 3 S3,3 = С3,3 - (U3 + V3) = 2 S3,5 = С3,5 - (U3 + V5) = 4
S4,2 = С4,2 - (U4 + V2) = 6 S4,4 = С4,4 - (U4 + V4) = 8 S4,6 = С4,6 - (U4 + V6) = 3 Имеем клетку (1, 1) с отрицательной оценкой, план не оптимален. Строим для этой клетки цикл.
Перемещаем по циклу груз величиной в 4 единиц, прибавляя эту величину к грузу в клетках со знаком "плюс" и отнимая ее от груза в клетках со знаком "минус". В результате перемещения по циклу получим новый план:
Целевая функция (транспортные расходы) z = 285. Значение целевой функции изменилось на 4 единицы по сравнению с предыдущим этапом. Проверим полученный план на оптимальность. Подсчитаем потенциалы. U1=0 V1 = C1,1 – U1 = 5 U4 = C4,1 – V1 = 3 V3 = C4,3 – U4 = 1
V5 = C4,5 – U4 = 2 U2 = C2,5 – V5 = 4 V2 = C2,2 – U2 = 3 V6 =C1,6 – U1 = 4 U3 = C3,6 – V6 = 3 V4 = C3,4 - U3 = 3 Для свободных клеток определим значения оценок (разностей между прямыми и косвенными тарифами). S1,2 = С1,2 - (U1 + V2) = 5 S1,3 = С1,3 - (U1 + V3) = 12 S1,4 = С1,4 - (U1 + V4) = 3 S1,5 = С1,5 - (U1 + V5) = 7
S2,1 = С2,1 - (U2 + V1) = 3 S2,3 = С2,3 - (U2 + V3) = 6 S2,4 = С2,4 - (U2 + V4) = 3 S2,6 = С2,6 - (U2 + V6) = 0
S3,1 = С3,1 - (U3 + V1) = 1 S3,2 = С3,2 - (U3 + V2) = 4 S3,3 = С3,3 - (U3 + V3) = 3 S3,5 = С3,5 - (U3 + V5) = 5
S4,2 = С4,2 - (U4 + V2) = 6 S4,4 = С4,4 - (U4 + V4) = 7 S4,6 = С4,6 - (U4 + V6) = 2 Так как все оценки Si,j ≥ 0, то полученный план является оптимальным, минимальные транспортные расходы равны 285.
ЗАДАЧА № 2 Имеется заявка на перевозку груза с условиями. Необходимо доставить груз нескольким потребителям, в рассматриваемом примере равные эксплуатационные условия в районе перевозки груза, тогда в качестве критерия решения задачи допустимо принять расстояние перевозки груза, что будет соответствовать минимальной стоимости для потребителя. Потребность в грузе первого пункта n3- 2т.; второго пункта n8-1т.; третьего пункта n10- 5т. Известны адреса клиентов, поставщика и их взаимное расположение; условия эксплуатации – город. Взаимное расположение поставщика и потребителей, расстояние между пунктами представлены на рис. 6. Число перестановок из w пунктов завоза (вывоза), включаемых в маршрут по w пунктам: Pw = w!, (11)
где w! – факториал целого положительного числа w, который равен произведению: w! = 1·2·3…· w. При трех пунктах груза количество возможных маршрутов М = w! = 3! = 1·2·3 = 6, таким образом, возможны шесть маршрутов доставки груза из пункта В. Выбор маршрута осуществляется по критерию «минимум затрат», чему соответствует минимум пробега. При наличии двух и более маршрутов одинаковой протяженности цели системы соответствует минимум грузооборота на маршруте. Результаты расчета пробега и грузооборота представлены в табл. 12. Схема транспортной сети, взаимное расположение пунктов, длинны звеньев, потребность грузов в развозочной системе представлены на рис. 6.
n8-q2 = 1т 8
159 км 67 км
n3- q1 = 2т В 134 км 3
81 км
190 км
10
n10- q3 = 5т
Рис. 6 . Схема транспортной сети, взаимное расположение пунктов, длинны звеньев, потребность грузов в развозочной системе
Вычислим транспортную работу: Р1 = 67∙8 + 159∙7 + 190∙5 = 2599 т·км; Р2 = 81∙8 + 190∙3 + 159∙1 = 1377 т·км; Р3 = 134∙8 + 190∙6 + 148∙1 = 2360 т·км;
Р4 = 134∙8 + 159∙6 + 148∙5 = 2766 т·км; Р5 = 81∙8 + 148∙3 + 159∙2 = 1410 т·км; Р6 = 67∙8 + 148∙7 + 190∙2 = 1952 т·км. Примем для дальнейшего проектирования системы маршрут №5 –В-10-8-3-В, поскольку ему соответствует минимальный пробег и грузооборот. Расчет результатов функционирования автомобиля в системе выполним, используя модель развозочной системы. Результаты представлены в табл. 13.
ВЫВОД При выполнении курсового проекта были решены следующие вопросы и задачи:
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

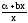 –
гипербола;
–
гипербола;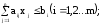

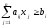 .
.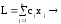 min
(max).
min
(max).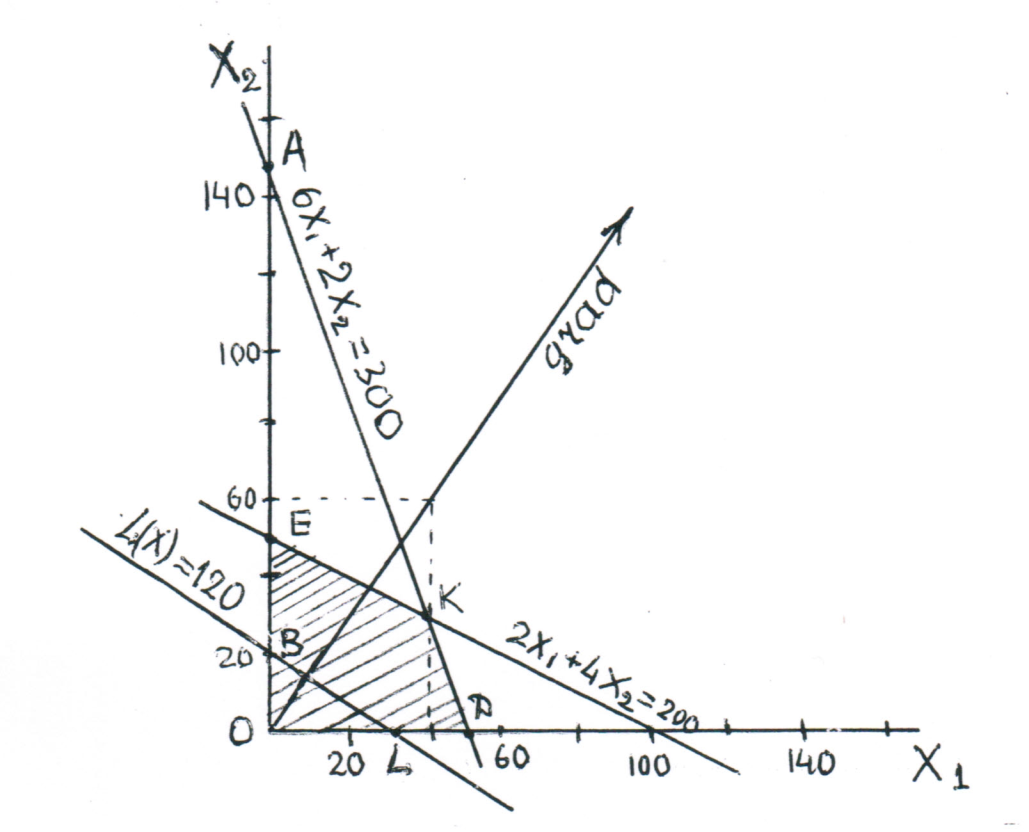
 ,
(1)
,
(1)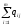 ,
где j=1,
2…n;
,
где j=1,
2…n;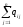 ,
где i=1,2…m.
,
где i=1,2…m.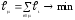


 ,
(6.3)
,
(6.3)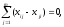 i=2, 3, …, m-1;
(6.4)
i=2, 3, …, m-1;
(6.4)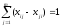 ;
(6.5)
;
(6.5)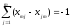 ;
(6.6)
;
(6.6)
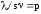 <
1,
(3)
<
1,
(3)