4 Зв'язність графів. Ейлерові та гамільтонові графи

4.1 Мета заняття

Ознайомлення на практичних прикладах з основними поняттями зв’язності графів, з їх метричними характеристиками. Вивчення способів визначення ейлеревих та гамільтонових графів. Ознайомлення з алгоритмами знаходження ейлерева циклу (ейлерева графа), гамільтонова шляху (гамільтонова графа).

4.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-8, 10-12] з наступних питань: поняття зв'язності графів, властивості зв'язних графів; метричні характеристики зв'язних графів; ейлереві графи; теорема Ейлера про наявність ейлерева циклу; алгоритм знаходження ейлерева циклу (теорема Флері); гамільтонові графи; ознаки існування гамільтонових циклів, шляхів і контурів.

Підготовка і виконання практичного заняття проводиться за два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень теми «Зв'язність графів. Ейлерові та гамільтонові графи»: маршрут; довжина маршруту; замкнений маршрут; ланцюг; простий ланцюг; цикл; дуга; орієнтований маршрут; шлях; контур; зв’язний граф; незв'язний граф; сильно зв’язний граф; підграф; компонента зв’язності; n-зв'язний граф; степінь зв'язності графа; число вершинної зв'язності; число реберної зв'язності; точка зчленування графа; міст; відстань між вершинами графа; діаметр графа; ексцентриситет вершини; радіус графа; центральна вершина графа; центр графа; грань (комірка) геометричного графа; необмежена грань (зовнішня грань); внутрішня грань; границя грані; ейлерів ланцюг; ейлерів цикл; ейлерів граф; власний ейлерів шлях; алгоритм знаходження ейлерева циклу (алгоритм Флері); гамільтонів шлях (гамільтонів ланцюг); гамільтонів граф.

Під час виконання першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.

Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, представлених у підрозділі 4.3, на основі запропонованих типових прикладів (див. підрозділ 4.4).

4.3 Контрольні запитання і завдання

4.3.1 Контрольні запитання

1. Дайте визначення зв'язного і незв'язного графів.

2. Що являє собою компонента зв'язності графа? Наведіть приклади компонент зв'язності.

3. Що називається степенем зв'язності графа?

4. Перелічить властивості зв'язних графів.

5. Наведіть приклади метричних характеристик зв'язних графів.

6. Якщо граф зв'язний і –число його вершин, то яка нижня оцінка для числа його ребер?

7. Дайте визначення ейлерева циклу (ейлерева ланцюга, замкненого ейлерева ланцюга).

8. Який граф називається ейлеревим?

9. Для розв’язання яких практичних задач використовується теорема Ейлера?

10. Поясніть використання алгоритму знаходження ейлерева циклу (теорема Флері).

11. Надайте визначення гамільтонова шляху (гамільтонова ланцюга), гамільтонова циклу.

12. Який граф називається гамільтоновим?

13. Надайте характеристику алгоритму Робертса-Флореса. Для яких цілей він використовується?

14. Назвіть основні ознаки існування гамільтонових циклів, шляхів і контурів.

15. Охарактеризуйте теорему (умову Дірака) для визначення гамільтонова графа.

4.3.2 Контрольні завдання

Завдання 1. Визначити, чи є для графа , який надається на рис. 4.1, маршрут ланцюгом, циклом, простим циклом, якщо маршрут задається як: 1); 2); 3); 4).

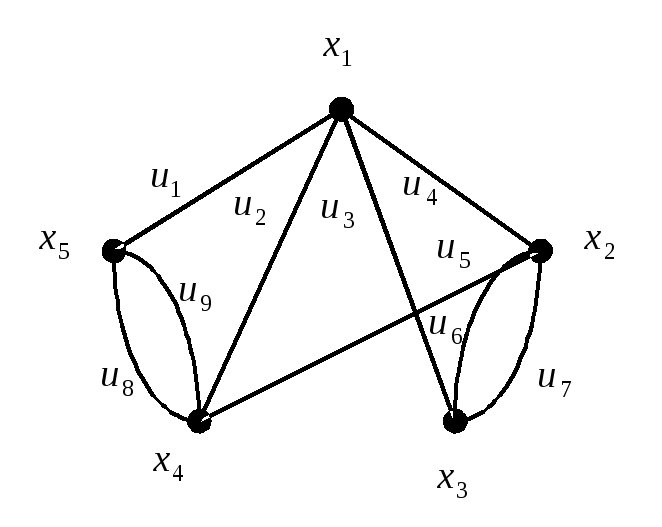
Рисунок 4.1 – Граф

Завдання 2. Який з наведених на рис. 4.2 орієнтованих графів є зв’язним? Який з графів є сильно зв’язним?

Рисунок 4.2

Завдання 3. Визначити число компонент зв’язності в графах та(рис. 4.3), якщо ці графи задаються таким чином

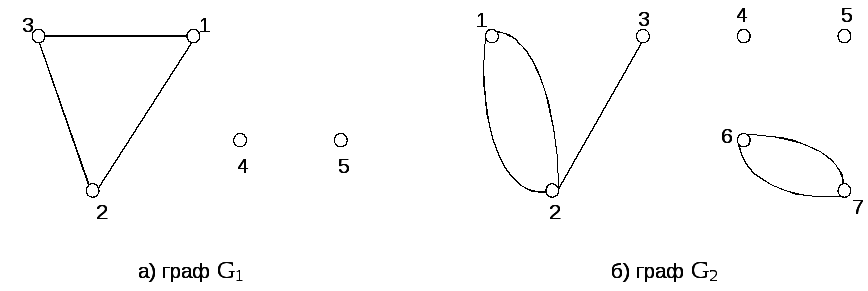
Рисунок 4.3

Завдання 4. Визначити компоненти зв’язності в графі (рис. 4.4) і знайти маршрути довжини три (три дуги), які виходять з вершини .

Рисунок 4.4

Завдання 5. Знайти в графі (рис. 4.5) всі точки зчленування і мости.

Рисунок 4.5

Завдання 6. Знайти такі метричні характеристики графа (рис. 4.6): ексцентриситети усіх вершин графа, діаметр графа, радіус графа, периферійні вершини графа, діаметральні ланцюги, центральні вершини графа, центр графа.

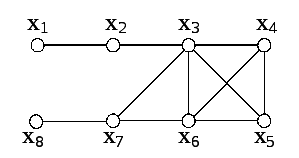
Рисунок 4.6

Завдання 7. Знайти для графа , який зображений на рис. 4.7, центр, радіус, діаметр, периферійні точки.

Рисунок 4.7

Завдання 8. Визначити, чи є графи і , які зображені на рис. 4.8, ейлеревими (мають ейлерів цикл).

Рисунок 4.8

Завдання 9. Серед графів, які зображені на рис. 4.9, знайдіть ті, які мають власний ейлерів шлях?

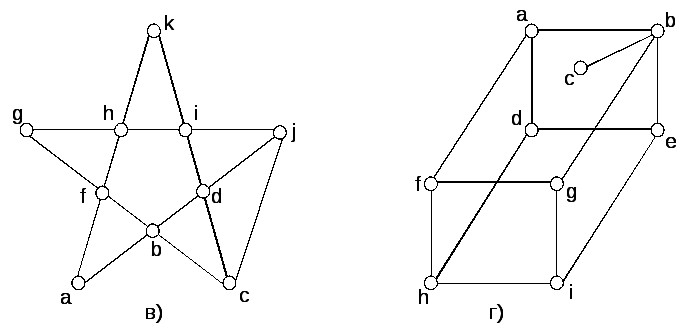
Рисунок 4.9

Завдання 10.

Поясніть, які з орієнтованих графів, що зображені на рис. 4.10, мають ейлерів цикл?

Рисунок 4.10

Завдання 11.

Найдіть гамільтонів цикл, якщо він існує, для кожного з графів, які зображені на рис. 4.11.

Рисунок 4.11

Завдання 12.

Нарисуйте наступні графи: а) ; б); в); г).

4.4 Приклади аудиторних і домашніх завдань

Завдання 1. Визначити, чи є для графа , який представлений на рис. 4.1, відповідний маршрут ланцюгом, простим ланцюгом, циклом, простим циклом, якщо маршрут заданий як: 1); 2); 3); 4); 5).

Розв'язок. Відповідно до визначення ланцюга, простого ланцюг, циклу, простого циклу одержимо: 1) простий цикл (всі вершини й ребра різні); 2) цикл (всі ребра різні, а вершини ні); 3) простий ланцюг; 4) маршрут (є однакові ребра й вершини); 5) простий ланцюг.

Завдання 2. Визначити число компонент зв’язності в графі , якщо граф задається таким чином (рис. 4.12)

Рисунок 4.12 – Граф , для якого визначається число компонент зв’язності

Розв’язок. Граф має дві компоненти зв’язності, в першу входять вершини , в другу .

Завдання 3. Розкласти орграф , який представлений на рис. 4.13, на сильно зв’язані компоненти.

Рисунок 4.13

Розв’язок. Граф розкладається на три сильно зв’язані компоненти ,,(рис. 4.14)

Рисунок 4.14

Завдання 4.

Знайти в графі , який надається на рис. 4.15, всі точки зчленування і мости.

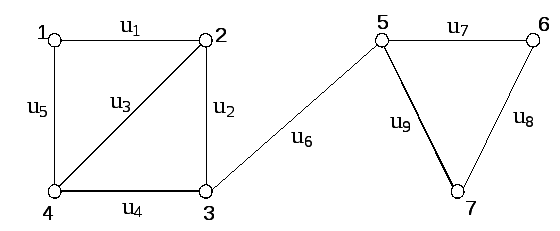
Рисунок 4.15

Розв’язок.

Послідовно розглянемо ребра графа, вилучаючи їх з графа. Тільки вилучення ребра приводить до збільшення числа компонент зв’язності, тому є мостом. Аналогічно розглядаємо вершини графа і находимо, що вершини 3 і 5 є точками зчленування, тому що вилучення їх з графа приводить до збільшення числа компонент зв’язності.

Завдання 5.

Знайти такі метричні характеристики графа (рис. 4.16): ексцентриситети усіх вершин графа, діаметр графа, радіус графа, периферійні вершини графа, діаметральні ланцюги, центральні вершини графа, центр графа.

Рисунок 4.16

Розв’язок.

Ексцентриситетом вершиниє відстань віддо найбільш віддаленої від неї вершини, тому,,. Максимальний з усіх ексцентриситетів є діаметром графа, тобто. Найменший з ексцентриситетів є радіусом графа, тобто. Вершинає периферійною, якщо її ексцентриситет дорівнює діаметру графа, тобто, тому периферійними вершинами графає вершиниі. Простий ланцюг, відстань між кінцями якої дорівнює, називається діаметральні ланцюги ом, тому діаметральними ланцюгами графає такі ланцюги:і. Вершинаназивається центральною вершиною графа, якщо на ній досягається мінімум ексцентриситетів, тобто, тому центральною вершиною графає вершина. Множина усіх центральних вершин графа є центром графа, тому центром графає.

Завдання 6.

Визначити, чи є граф , який зображений на рис. 4.17, ейлеревим.

Рисунок 4.17

Розв’язок.

Використаємо теорему Ейлера: граф є ейлеревим (містить ейлерів цикл) тоді і тільки тоді, коли він зв’язний і степені всіх його вершин – парні.

Граф є зв’язним. Степені його вершин такі:,,. Граф не є ейлеревим, тому що не усі степені вершин є парними.

Завдання 7.

Чи має граф, який зображений на рис. 4.18 власний ейлерів шлях?

Рисунок 4.18

Розв’язок.

Використаємо наступну теорему: граф (мультограф або псевдограф) має власний ейлерів шлях тоді й тільки тоді, коли він зв’язний і рівно дві його вершини мають непарний степінь. Граф, зображений на рис. 4.18, зв’язний, має власний ейлерів шлях, тому що рівно дві його вершини (і) мають непарну степінь, тобто.

Завдання 8.

Чи має орієнтований граф, який зображений на рис. 4.19, ейлерів цикл?

Рисунок 4.19

Розв’язок.

Використаємо наступну теорему: орієнтований граф має ейлерів цикл тоді й тільки тоді, коли він зв’язний, і півстепені виходу та заходу у вершині рівні. Орієнтований граф, який зображений на рис. 4.19, не містить ейлерів цикл, тому що півстепені виходу та заходу у вершинахіне дорівнюють відповідно один одному.

Завдання 9.

Найдіть гамільтонів цикл, якщо він існує, у графі , який зображений на рис. 4.20.

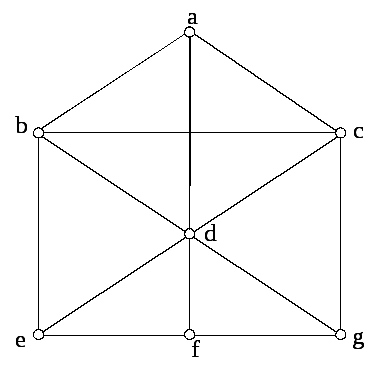
Рисунок 4.20

Розв’язок.

Гамільтонів цикл для графа буде таким.