6 Відшукання найкоротших відстаней

МІЖ ВЕРШИНАМИ ГРАФА (МЕРЕЖІ)

6.1 Мета заняття

Ознайомлення з основними методами та алгоритми розв’язку задач відшукання оптимальних шляхів у орієнтованих графах (алгоритмами Дейкстри, Форда, Флойда, Данцига). Вивчення формального опису алгоритму Дейкстри побудови найкоротших шляхів із вершини графа. Використання алгоритму Дейкстри для знаходження відстані між парами вершин у орієнтованих і неорієнтованих графах, для побудови остовного орієнтованого дерева графа.

6.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-8, 10-12] з таких питань: постановка задачі відшукання найкоротших відстаней між вершинами графа (мережі) із заданими вагами ребер; задача пошуку оптимальних шляхів у орієнтованих мережах; економічний зміст задачі відшукання найкоротших відстаней між вершинами графа (мережі) із заданими вагами ребер; алгоритми розв’язку задач відшукання оптимальних шляхів у орієнтованих мережах (алгоритми Дейкстри, Форда, Флойда, Данцига);; складність алгоритму Дейкстри.

Підготовка і виконання практичного заняття проводиться у два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: шлях; маршрут; орієнтований маршрут; довжина (вага) дуги (ребра); довжина маршруту; зважений граф; відстань між вершинами графа; мінімальна сума ваг дуг; найкоротший шлях з вершини до вершиниграфа.

При виконанні першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень. Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, представлених у підрозділі 6.3, на основі запропонованих типових прикладів (див. підрозділ 6.4).

6.3 Контрольні запитання і завдання

6.3.1 Контрольні запитання

1. Який граф називається зваженим графом?

2. Що являє собою вага (довжина) ребра графа?

3. Наведіть постановка задачі відшукання найкоротших відстаней між вершинами графа (мережі) із заданими вагами ребер.

4. Який економічний зміст мають задачі відшукання найкоротших відстаней між вершинами графа (мережі) із заданими вагами ребер?

5. Поясніть ідею алгоритму Е. Дейкстри, який використовується для розв’язання задачі відшукання найкоротших відстаней між вершинами графа.

6. Наведіть формальний опис алгоритму Дейкстри побудови найкоротших шляхів із вершини графа.

7. Як можна оцінити складність алгоритму Дейкстри?

8. Якщо у графі є дуги з від’ємними і додатними вагами, чи знаходить алгоритм Дейкстри найкоротший шлях?

9. Поясніть, чим відрізняється алгоритм Форда від алгоритму Дейкстри при побудові найкоротших шляхів у графі.

10. Опишіть алгоритм Флойда пошуку найкоротших шляхів між всіма парами вершин графа.

11. Опишіть алгоритм Данцига пошуку найкоротших шляхів графа.

6.3.2 Контрольні завдання

Завдання 1. Нехай потрібно знайти відстань до всіх вершин графа (рис. 6.1) від його вершини. Ваги дуг, що дорівнюють цілим числам, вказано на рис. 6.1.

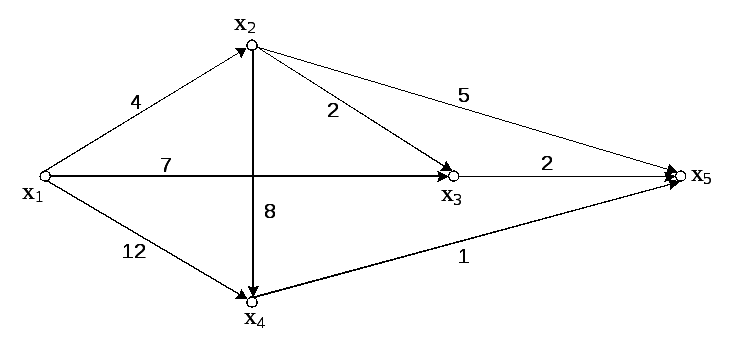
Рисунок 6.1

Завдання 2. За допомогою алгоритму Дейкстри побудувати остовне дерево найкоротших шляхів із вершини до вершин графа, який представлений на рис. 6.2. Кожне орієнтоване ребро з вагоюрозглядається як пара протилежно спрямованих дуг з однаковими вагами.

Рисунок 6.2

Завдання 3. Знайти відстань від вершини до всіх інших вершин і найкоротший шлях між вершинамиіорграфа, який задано наступною матрицею відстаней

,

де – довжина (вага) дуги між вершиноюі вершиною.

Завдання 4. Найти відстань від вершини до вершиниі всі найкоротші шляхи між цими вершинами для орграфа, який задається матрицею відстаней

.

6.4 Приклади аудиторних і домашніх завдань

Завдання 1. Нехай задається зважений граф (рис. 6.3), множина вершин якого є, ваги дуг, що дорівнюють цілим числам, вказано на рис. 6.3. Необхідно знайти найкоротший шлях між вершинамиі, вказати найкоротші шляхи меншої довжини з вершинидо відповідних вершин.

Рисунок 6.3

Розв’язок.

Введемо позначення: – вага (довжина) дуги,– довжина-шляху або позначка вершинина даному кроці,– довжина-шляху або позначка вершинина попередньому кроці.

Цикл 1.

Крок 1. Привласнення початкових значень.

–постійна позначка; фарбується.

–тимчасовів позначкеи вершин . Припускаємо, що.

Крок 2. Розгляд вершини (). Оновлення позначок.

.

Крок 3. Розгляд вершини (). Перетворення позначки на простійну.

.

Вершина одержує постійну позначку, вершина– фарбується разом з дугою. Поточне деревонайкоротших шляхів з вершинимістить вершиниі дугу(рис. 6.4). Припускаємо .

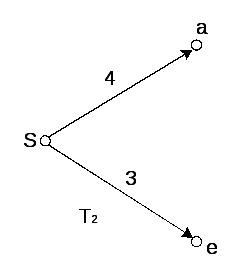
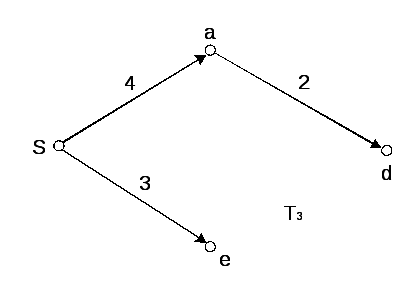
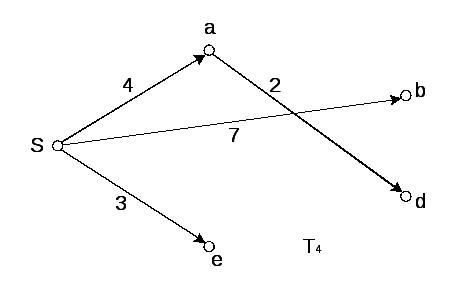
Рисунок 6.4 – Зростаючі орієнтовані дерева найкоротших шляхів

Цикл 2.

Крок 2. Розгляд вершини (). Оскільки, переходимо до кроку 2 при. Проводимо оновлення позначок.

.

Крок 3. Розгляд вершини (). Перетворення позначки на простійну.

.

Вершина одержує постійну позначку, вершина– фарбується разом з дугою. Поточне дерево найкоротших шляхівскладається з вершині дуг,(див. рис. 6.4).

Припускаємо .

Цикл 3.

Крок 2. Розгляд вершини (). Оскільки, переходимо до кроку 2 при. Проводимо оновлення позначок.

.

Крок 3. Розгляд вершини (). Перетворення позначки на простійну.

.

Вершина одержує постійну позначку, вершинаі дугафарбується. Поточне дерево найкоротших шляхівскладається з вершині дуг,,(див. рис. 6.4).

Припускаємо .

Цикл 4.

Крок 2. Розгляд вершини (). Оскільки, проводимо оновлення позначок.

.

Крок 3. Розгляд вершини (). Перетворення позначки на простійну.

.

Вершина одержує постійну позначку, і фарбується разом з дугою. Поточне дерево найкоротших шляхівскладається з вершині дуг,,,(див. рис. 6.4).

Припускаємо .

Цикл 5.

Крок 2. Розгляд вершини (). Оскільки, проводимо оновлення позначок.

.

Крок 3. Розгляд вершини (). Перетворення позначки на простійну.

.

Вершина одержує постійну позначку, і фарбується разом з дугою. Поточне дерево найкоротших шляхівмістить всі вершини графа, тобто вершиниі дуги,,,,(див. рис. 6.4). Деревоє остовним деревом у.

Зупинка.

Найкоротший шлях із доє,,. Він не є єдиним. Таку ж довжину 8 має шлях,,.