В. Д. Бертяев, Л. А. Булатов, В. В. Глаголев, В. И. Латышев, А. Г. Митяев. ЭВМ в курсе теоретической

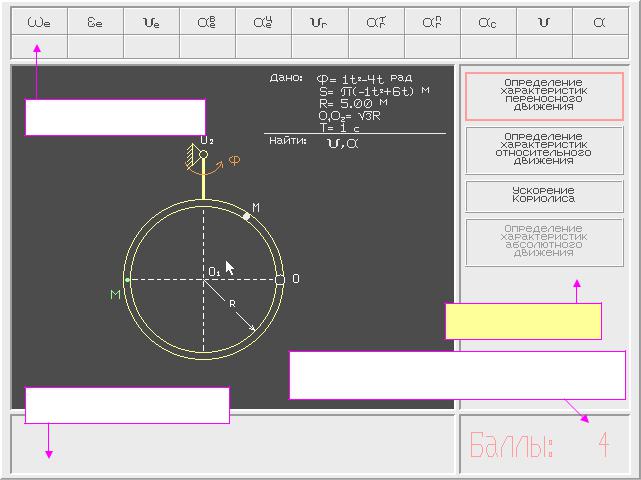
oтаблица результатов, в которую заносятся значения искомых величин после контроля их значений;

o основное меню;

o поле вопросов и ответов.

Взаимодействие студента с программой осуществляется с помощью основного меню, состоящего из четырех блоков, и некоторых вспомогательных меню (в их числе, — меню блоков). В ходе решения задачи студент имеет возможность проводить следующие графические операции:

1)Изображать скорости и ускорения точки М.

2)Показывать направления вращения и углового ускорения тела А.

На рис. 1.13 приведено состояние экрана после определения положения точки M в заданный момент времени.

Таблица результатов

Основное меню

За правильное определение положения точки M в момент времени T=1c начислено 4 балла

Поле вопросов и ответов

Рис. 1.13

21

Студент самостоятельно намечает порядок решения задачи, за исключением первого шага: программа директивно предлагает ему определить положение точки M относительно тела A в момент времени T. Для проведения вычислений программа имеет встроенный калькулятор, который вызывается клавишей F2 при любом состоянии экрана. Отключение калькулятора осуществляется клавишей Esc, которая также используется в программе для перехода от одного состояния в другое (например, для возврата из режима определения характеристик переносного движения к основному меню). Программа контролирует 29 действий студента. Все действия студента по решению задачи оцениваются в баллах. Максимальная оценка за правильно решенную задачу – 100 баллов.

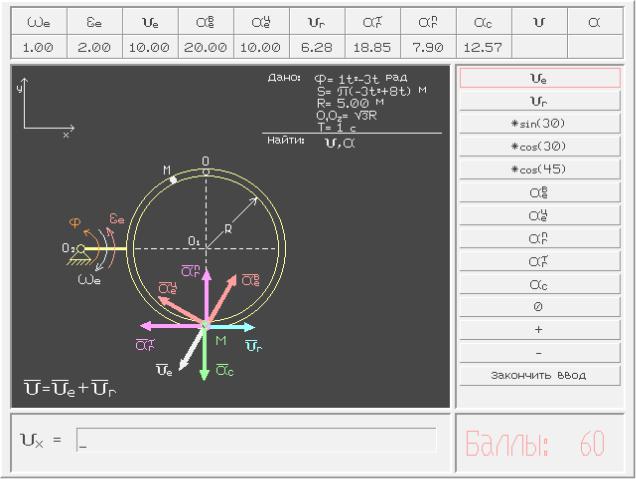
Рис. 1.14

На рис. 1.14 приведено состояние экрана в процессе решения задачи: построена расчетная схема, найдены характеристики переносного и относительного движений точки, идет определение проекции абсолютной скорости на ось x.

22

ГЛАВА 2. ИСПОЛЬЗОВАНИЕ ПАКЕТА MATHCAD ПРИ РЕШЕНИИ ЗАДАЧ ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ С АНАЛИЗОМ ПОВЕДЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ

Усвоение курса теоретической механики требует приобретения твердых навыков в решении задач, что наиболее успешно может быть достигнуто при выполнении курсовых работ.

Вэтой главе рассматриваются примеры выполнения трех курсовых работ

сэлементами исследования по всем основным разделам программ, утвержденных Министерством образования Российской федерации (кинематика, статика, динамика). Выполнение курсовых работ осуществляется с использованием математического пакета Mathcad, который представляет собой эффективное средство для аналитических преобразований и численного решения инженерных и физических задач.

Область его применения простирается от простейших вычислений до расчета сложных задач в различных отраслях знаний. С помощью Mathcad можно с успехом решать задачи механики абсолютно твердых и деформируемых тел. Пакет имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства графики.

Использование Mathcad в теоретической механике позволяет проводить анализ поведения механических систем в соответствии с поставленной задачей, что дает возможность решать реальные инженерные задачи учащимися младших курсов не знакомых еще с численными методами и программированием.

В предлагаемых примерах курсовых работ основное внимание уделено решению задач, специально подобранных для того, чтобы дать возможность после изучения изложенного материала, самостоятельно решать более сложные и математически трудоемкие задачи механики. Предполагается, что студент имеет базовые знания в курсе информатики.

23

2.1. КИНЕМАТИКА ПЛОСКИХ МЕХАНИЗМОВ

Широкое применение в технике получили плоские четырех и шестизвенные механизмы. Кинематическое исследование этих механизмов играет важную роль на этапе предварительного проектирования узлов и звеньев сложных машин. Рассмотрим вопрос о кинематическом анализе таких механизмов. Задача кинематического исследования сводится к совместному решению уравнений геометрических связей, с последующим дифференцированием этих уравнений для нахождения скоростей и ускорений.

2.1.1. ПОСТАНОВКА ЗАДАЧИ.

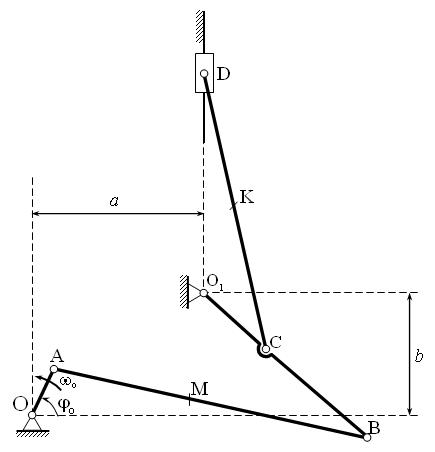
Провести кинематическое исследование плоского шарнирного многозвенного механизма с одной степенью свободы, для которого известны все геометрические размеры и закон движения ведущего звена (рис. 2.1.1).

Рис. 2.1.1 Схема механизма и исходные данные для расчета.

24

Определить законы движения всех звеньев механизма, угловые скорости и ускорения ведомых звеньев, а также линейные скорость и ускорение звена, движущегося поступательно. Вычислить скорости и ускорения всех узловых точек механизма, а также точек M и K , в зависимости от значения угла поворота ве-

дущего звена ϕO (t ). Произвести визуализацию механизма, изобразить траекто-

рии, векторы скоростей и ускорений всех его заданных точек, если даны: o геометрические размеры

OA =15 см, AM = 42 см,	AB = 97 см,	O1B = 60	см,		O1C = 45	см,
CD =86 см,	CK = 47 см,	a = 50	см,		b = 37	см;
o закон движения ведущего звена механизма
	ϕO (t ) =ϕo +ωo t ,
где ϕo = 0 — начальное значение угла поворота; ωo =			π	18	c−1 — угловая ско-
рость ведущего звена.

Уравнения геометрических связей.

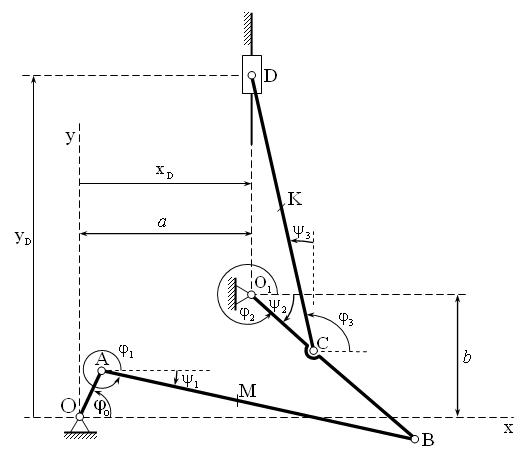
Изобразим плоский механизм в произвольном положении (рис. 2.1.2).

В качестве системы отсчета примем правую декартову систему координат. Начало системы координат расположим в подшипнике O . Положительные углы поворота в этом случае направлены против часовой стрелки.

Изобразим углы поворота звеньев ϕk , k =1,2,3 , отсчитывая их от гори-

зонтальной оси Ox в положительном направлении.

В состав данного многозвенного механизма входят:

oдва кривошипа OA и O1B, которые совершают вращательное движение во-

круг неподвижных осей перпендикулярных плоскости xOy и проходящих

через точки O и O1 соответственно;

oдва шатуна AB и CD , совершающих плоскопараллельное движение в плоскости xOy ;

25

oползун D движется возвратно-поступательно вдоль направляющей параллельной оси Oy ;

o неподвижное звено OO1 .

Рис. 2.1.2. Расчетная схема механизма

Для составления уравнений геометрических связей найдем точки механизма, траектории которых известны. К этим точкам относятся шарниры A , B , C и D . Точки A , B и C движутся по окружностям радиусов OA , O1B и O1C

соответственно, а ползун D — по прямолинейной траектории параллельной оси Oy (рис. 2.1.2).

Шарнир A принадлежит одновременно шатуну AB и кривошипу OA , для которого известен закон вращательного движения и, следовательно, закон движения точки A определен. Шарнир B принадлежит одновременно шатуну AB и кривошипу O1B, а шарнир C — шатуну CD и кривошипу O1B. Из двух точек C и B , одновременно принадлежащих кривошипу O1B, одна является

26

зависимой, т.е. определение закона движения одной точки приводит к возможности определения закона движения для другой.

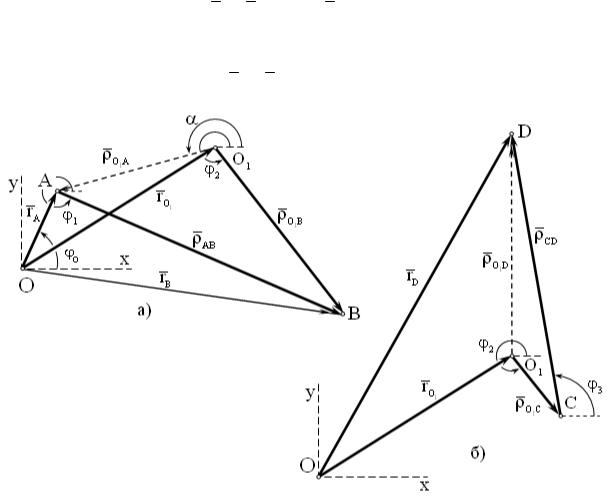
Так как закон плоскопараллельного движения твердого тела можно определить по двум любым точкам этого тела, в качестве базовых точек, при составлении уравнений геометрических связей, примем точки B и D .

Построим для этих точек векторные контуры, с помощью которых можно составить уравнения геометрических связей (рис. 2.1.3):

для точки B (рис. 2.1.3 а)

r

B =

r

A + ρAB

=

r

O

+ ρO B ,

(1)

1

1

для точки D (рис. 2.1.3 б)

r

D

=

r

O

+ ρO C + ρCD .

(2)

1

1

Рис. 2.1.3. Векторные контуры для базовых точек механизма

Для получения уравнений геометрических связей в координатной форме соотношения (1), (2) преобразуем с использованием аналитического процессора пакета Mathcad, так как показано ниже.

27

OA cos (φO(t))			AM cos (φ1(t))
RA (t) := OA sin(φO(t))			ρAM (t) := AM sin(φ1(t))
	0			0
O1B cos (φ2(t))			O1C cos (φ2(t))
ρB(t) := O1B sin(φ2(t))			ρC(t) := O1C sin(φ2(t))
	0			0
CK cos (φ3(t))			CD cos (φ3(t))
ρCK(t) := CK sin(φ3(t))			ρCD(t) := CD sin(φ3(t))
	0			0

AB cos (φ1(t))
	AB sin(φ1(t))
ρAB(t) :=
	0
a
RO1(t) := b
	0

	a
RD(t) :=	Y(t)
	0

Выражения геометрических связей в векторной форме

ORIGIN := 1

R1(t) := RA (t) + ρAB(t) − RO1(t) − ρB(t)

R2(t) := RO1(t) + ρC(t) + ρCD(t) − RD(t)

R(t) := stack submatrix (R1(t)),1 ,2 ,1 ,1 ,submatrix (R2(t)),1 ,2 ,1 ,1

substitute ,φO(t)

φO

OA cos (φ

) + AB cos (φ

) − a − O1B cos (φ

2

)

O

1

substitute ,φ

1

(t)

φ

1

sin(

φ

O)

+

φ

1)

−

b

−

φ

2)

R(t)

OA

AB sin(

O1B sin(

→

O1C cos (φ2) + CD cos (φ3)

substitute ,φ2(t)

φ2

substitute ,φ3(t)

φ3

b +

O1C sin(φ2) + CD sin(φ3) − yD

substitute ,Y(t) yD

Приравняв правую часть выражения R(t ) нулю, получим уравнения гео-

метрических связей в координатной форме

OA cos(ϕ			O	)+ AB cos(ϕ )− a −O B cos(ϕ			)
				1	1	2
OA sin(ϕO )+ AB sin (ϕ1 )−b −O1B sin(ϕ2 )								= 0 .	(3)
	O C cos(ϕ			)+CD cos(ϕ	)
	1		2	3
		sin(ϕ2 )+CD sin (ϕ3 )− yD
b +O1C

В уравнениях (3) задаваемой функцией является закон вращения ведуще-

го звена ϕO (t ), а определяемыми функциями времени являются

ϕ1 (t), ϕ2 (t), ϕ3 (t), yD (t).

Система (3) представляет замкнутую систему уравнений для определения законов движения всех звеньев многозвенного механизма.

28

Решение уравнений (3) можно найти различными методами, как аналитическими, так и численными. Численные решения уравнений подобного рода реализуются с использованием встроенных процедур.

Определение законов движения звеньев механизма

Аналитический метод

Аналитические методы при решении нелинейных систем уравнений типа

(3) применяются в тех случаях, когда необходимо получить (если это возможно) выражения для искомых функций в параметрическом виде.

Для нахождения законов движения звеньев механизма в аналитической форме запишем первые два уравнения системы (3) в следующем виде

(рис. 2.1.3 а, рис. 2.1.2, рис. 2.1.4)

AB cos(ϕ1 )−O1B cos(ϕ2 ) = a −OA cos(ϕO ) = −xO A = −O1 A cos α,

1

(4)

AB sin (ϕ1 )−O1B sin (ϕ2 )= b −OA sin (ϕO )= −yO A = −O1 A sin α,

1

где xO A = O1A cosα,

yO A = O1A sin α — проекции вектора ρO A на оси коорди-

1

1

1

нат; O1A — его модуль (рис. 2.1.4)

O A = x

2

+ y

2 = O A2

+OA2

− 2 OA OO cos(ϕ

O

− β );

1

O A

O A

1

1

1

1

α — угол, определяемый выражениями

cos α =

OA cos(ϕO )− a

, sin α =

OA sin(ϕO )−b

,

O1 A

O1A

OO = a2 +b2

, β = arctg b

— модуль и направление вектора

r

.

1

O1

a

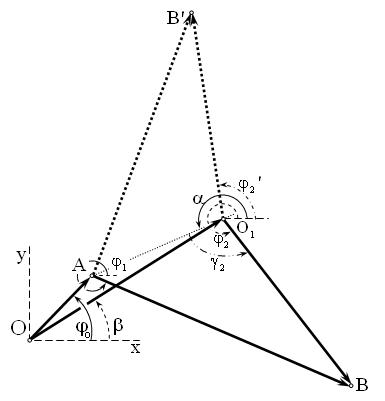
Для нахождения угловой координаты ϕ2

приведем уравнения (4) к виду

AB cos(ϕ1 )= O1B cos(ϕ2 )−O1 A cos α,

AB sin(ϕ1 )= O1B sin (ϕ2 )− O1 A sin α,

и, воспользовавшись тригонометрической формулой cos2 ϕ +sin2 ϕ =1, получим

29

AB2 = O1B2 +O1 A2 − 2 O1B O1 A [cosϕ2 cos α +sinϕ2 sin α].

Используя формулы приведения, найдем

cos(ϕ2 −α)=	O B2	+O A2	− AB2	= cos γ	2 .
	1	1
	2 O1B O1 A

Так как cos γ2 является четной функцией углового аргумента, то угол ϕ2 может иметь два значения ϕ2 =γ2 +α илиϕ2 =γ2 −α , что соответствует двум положе-

нием четырехзвенника OABO1 относительно O1 A при одной и той же угловой координате ведущего звена ϕ (рис. 2.1.4).

Рис. 2.1.4 Определение угловых координат звеньев Учитывая начальное положение механизма (рис. 2.1.2) принимаем

ϕ2		2	+O1 A	2	− AB	2	(5)
	=α + arccos O1B					.
		2 O1B O1 A

Для нахождения угловой координаты ϕ1 уравнения (4) перепишем в сле-

дующем виде

30