В. Д. Бертяев, Л. А. Булатов, В. В. Глаголев, В. И. Латышев, А. Г. Митяев. ЭВМ в курсе теоретической

AB cos(ϕ1 )+O1 A cos α = O1B cos(ϕ2 ),

AB sin(ϕ1 )+O1 A sin α = O1B sin(ϕ2 ).

Используя процедуру, изложенную выше, получим

AB2 +O A2 + 2 AB O A cos(ϕ )cos α +sin(ϕ )sin α = O B2 .

1

1

1

1

1

Окончательно, угловая координата ϕ1 равна

ϕ1 =α + arccos

2

−O1 A

2

− AB

2

(6)

O1B

.

2 AB O1 A

Для нахождения остальных неизвестных величин используем оставшиеся

два уравнения системы (3). Из третьего уравнения (3) найдем угловую коорди-

нату звена CD

O C

(7)

ϕ3 = arccos −

1

cos(ϕ2 ) ,

CD

а из четвертого — вертикальную координату ползуна D

yD = b +O1C sin(ϕ2 )+CD sin(ϕ3 ).

(8)

Уравнения (5) — (8) позволяют определить угловые координаты звеньев

совершающих вращательные и плоскопараллельные движения, а также закон

движения звена движущегося поступательно.

Реализация найденного решения в пакете Mathcad представлена ниже.

ORIGIN := 1

Закон движения ведущего звена — кривошипа ОА

φ0(t) := φo + ωo t

α (t) := angle

(

OA cos

φ

0

(t)

)

− a ,OA sin

(

φ

0

(t)

)

− b

(

)

b

2

2

2

2

2

(φ0(t) − β)

β := atan

− 2 OA

a

O1A(t) :=

a

+ b +

OA

a + b

cos

Законы движения ведомых звеньев механизма

2

AB

2

− O1A(t)

2

O1A(t)

2

2

− AB

2

φ1(t) := α (t) + acos

O1B −

φ2(t) := α (t) + acos

+ O1B

2 O1A(t) AB

2 O1A(t) O1B

φ3(t) := acos

−

O1C

cos

(φ2

yD(t) := b + O1C sin (φ2(t)) + CD sin (φ3(t))

CD

(t))

При вычислении вспомогательного угла α

используется встроенная в

Mathcad функция angle(x, y), которая возвращает в радианах значение угла на-

31

клона вектора, заданного своими проекциями x и y относительно положи-

тельного направления оси Ox . Применение данной функции возможно в последних версиях Mathcad. Поэтому при работе со старыми версиями требуется учитывать характерные особенности любого численного метода, связанного с нахождением угловых координат при помощи обратных тригонометрических функций.

α (t) :=	s ←		OA sin (φ0(t)) − b
				O1A(t)
	c ←		OA cos(φ		0(t)) − a
				O1A(t)
						s ≥ 0 c ≥ 0
	a ←			asin (s)	if
				acos(c)	if	s ≥ 0 c ≤ 0
				2 π + asin (s)			if			s ≤ 0 c ≥ 0
				2 π − acos(c)			if			s ≤ 0 c ≤ 0

Рис. 2.1.4. Вычисление угла α без использования функции angle

Так как, при применении функции arccos(ϕ) угол ϕ вычисляется в ин-

тервале −π≤ ϕ≤ π, а при использовании функции arcsin(ϕ) — в интервале

−π/ 2 ≤ ϕ ≤ π/ 2 , необходимо строить дополнительную процедуру вычисления угловой координаты, учитывающую разные знаки тригонометрических функций, так как это показано на рис. 2.1.4.

Численный метод

При использовании численной процедуры решения уравнений типа (3), в которых неизвестные величины являются аргументами тригонометрических (периодических) функций следует использовать такие переменные, которые исключают двойственность решения системы уравнений.

Например, на рис. 2.1.2 положение звена AB можно характеризовать двумя углами: положительным ϕ1 и отрицательным ψ1 . В силу вышесказанно-

32

го, рекомендуется в качестве аргументов тригонометрических функций применять угловые координаты, изменяющиеся в интервале −π2 ≤ϕ ≤π2 .

Решение системы уравнений (3) в пакете Mathcad будем искать с использованием встроенной процедуры–функции Find в блоке решенийGiven .

ORIGIN := 1

Закон движения ведущего кривошипа ОА

φ0(t) := φo + ωo t

Начальное приближение углов поворота звеньев и ползуна

ψ1 := 0

ψ2 := 0.

ψ3 := 0

yD := 2 b

Блок решения системы нелинейных уравнений

Given

cos (

φ

0

(τ)

)

+

π + ψ

1)

−

a

−

π + ψ

2)

OA

AB cos (2

O1B cos (2

sin(

φ

0

(τ)

)

+

π + ψ

1)

−

b

−

π + ψ

2)

OA

AB sin(2

O1B sin(2

O1C cos (2 π

) + CD cos

π

0

+ ψ

+ ψ

3

2

2

O1C sin(2 π + ψ

) + CD sin

π + ψ

b +

3

− y

D

2

2

Поиск решения системы уравнений

ψ(τ) := Find (ψ1 ,ψ2 ,ψ3 ,yD)

Создание модели механизма

X0(τ) := (0 a )

Y0(τ) := (0 b )

X1(τ) := (0

OA cos(φ0(τ))

O1B cos(2 π + ψ(τ)2)+ a

a

a + O1C cos(2 π + ψ(τ)2)

a )

Y1(τ) := (0

OA sin (φ0(τ))

O1B sin (2 π + ψ(τ)2) + b

b

b + O1C sin (2 π + ψ(τ)2)

ψ(τ)4 )

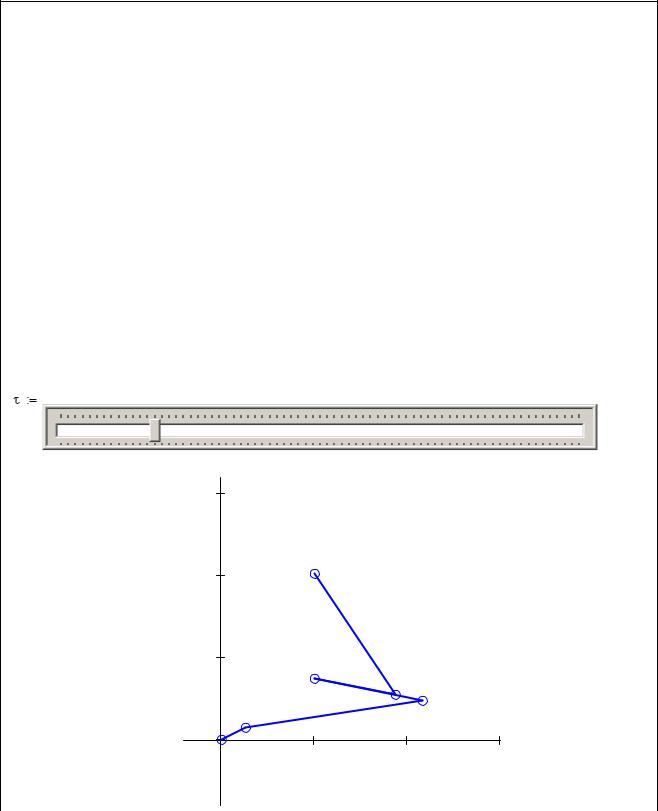
Изображение механизма на рисунке

t := 0.5τ

150

100

50

0

50

100

150

33

φ0(t)	= 30		ψ1(t)	= 9.7968		ψ2(t)
deg			deg			deg
	40
	20
Ψ1
Ψ2	0	90	180		270	360
Ψ3	20
	40
	60
			φ

= −12.5084

yD

	ψ3(t)	= 30.7195		yD(t) = 101.1861
	deg
105
100
95
90
85
80	0	90	180	270	360
			φ

Особое внимание при численном нахождении решения нелинейных систем уравнений следует обратить на правильное задание начальных приближений. В этом может помочь отображение рассчитываемого механизма на графике, создаваемого заданием координат его узловых точек X1 , Y1 , либо графики изменения вычисляемых угловых и линейных координат звеньев.

На рис. 2.1.5 представлен пример неудачного выбора начального приближения для координаты yD , величина которого равна yD := 3 b .

150

100

50

0

50

100

150

34

	150					180
	100					160
Ψ1	50					140
Ψ2						yD
Ψ3	0	90	180	270	360	120
	50					100
	100					80	0	90	180	270	360
			φ						φ

Рис. 2.1.5 Пример неудачного выбора начального приближения.

Определение угловых и линейных скоростей и ускорений звеньев

Для определения угловых и линейных скоростей звеньев механизма продифференцируем по времени уравнения геометрических связей (3). Дифференцирование уравнений произведем в пакете Mathcad c помощью функции пользователя "Diff_v", которая позволяет производить дифференцирование элементов матрицы произвольного размера. На рис. 2.1.6 показано применение данной функции.

Перенося слагаемые с неизвестными в одну сторону, получим

−AB sin(ϕ1 )ω1 +O1B sin (ϕ2 )ω2	= OA sin(ϕO )ω0 ,
AB cos (ϕ1 )ω1 −O1B cos(ϕ2 )ω2	= −OA cos(ϕO )ω0	,
−O1C sin(ϕ2 )ω2 −CD sin(ϕ3 )ω3	= 0,	(9)

O1C cos(ϕ2 )ω2 +CD cos(ϕ3 )ω3 −vD = 0.

Так как данная система уравнений является линейной относительно неизвестных угловых и линейных скоростей звеньев, то решение ее в пакете Mathcad можно выполнить не только с помощью функций–процедур "Find" и "Minerr", но и с использованием функции "lsolve", а также прямым матричным методом. Применение процедур "Find" и "Minerr" требует задания начальных условий, что является избыточным при решении систем линейных алгебраиче-

35

ских уравнений. Поэтому рационально решать такую задачу либо с помощью функции "lsolve", либо прямым методом.

v := Diff_v(R ,t ,1)

substitute ,d φO(t)

ωo

dt

substitute ,d φ1(t)

ω1

dt

−OA sin(φ ) ω

− AB sin(φ

) ω

+ O1B sin(φ ) ω

o

1

1

2

d

O

2

substitute ,dtφ2(t)

ω2

OA cos (φ ) ω

o

+ AB cos (φ

1

) ω

1

− O1B cos (φ

) ω

2

v

0

→

O

2

0

substitute ,d φ3(t)

−O1C sin(φ2) ω2 − CD sin(φ3) ω3

ω3

dt

O1C cos (φ2) ω2 + CD cos (φ3) ω3 − VD

substitute ,d Y(t)

V

dt

D

substitute ,φO(t)

φO

substitute ,φ1(t)

φ1

substitute ,φ2(t)

φ2

substitute ,φ3(t)

φ3

simplify

Рис. 2.1.6 Аналитические преобразования для нахождения скоростей звеньев

Для решения системы уравнений (9) представим ее в матричной форме

				A Xv = B,						(10)
где	−AB sin(ϕ1 )		O1B sin (ϕ2 )				0		0
		AB cos (ϕ )	−O B cos(ϕ			)	0		0
	A =	1	1	2		)	−CD sin(ϕ	)
		0	−O C sin(ϕ						0
		0	1		2	)	3	)
			O C cos(ϕ				CD cos(ϕ		−1
			1	2			3

—матрица коэффициентов левых частей уравнений,

ω1

X= ω2 — вектор неизвестных угловых и линейных скоростей звеньев,

vω3vD

36

Решение уравнений (10) будет иметь вид

Xv = A−1 B. (11)

Для определения угловых и линейных ускорений звеньев механизма дважды продифференцируем по времени уравнения геометрических связей (3). Процедуру дифференцирования произведем в пакете Mathcad c помощью функции пользователя "Diff_v". На рис. 2.1.7 показано применение данной функции.

Перенося слагаемые с неизвестными в одну сторону и, представляя, как и ранее, линейную относительно угловых и линейных ускорений звеньев, систему уравнений в матричной форме, получим

	OA sin(ϕ)ω
	−OA cos(ϕ)ω0		— вектор правых частей уравнений.
B =	0
	0
	0

							A Xa	= C.			(12)
где			AB cos(ϕ2 )ω12 −O1B cos(ϕ2 )ω2					2 +OA cos(ϕ)ω0	2
								2 −OA sin(ϕ)ω0
C =			AB sin(ϕ2 )ω12 −O1B sin(ϕ2 )ω2							2
			O1C cos(ϕ2 )ω2			2 +CD cos(ϕ3 )ω32
						2		2
			O1C sin(ϕ2 )ω2				+CD sin (ϕ3 )ω3
— вектор правых частей уравнений;
			ε1
X				ε
		=		1	— вектор неизвестных угловых и линейных ускорений звеньев.
	a			ε
				1
			aD
Решение уравнений (12) будет иметь вид
							Xa = A−1 C				(13)

Таким образом, решения (11) позволяют определить угловые и линейные скорости всех звеньев механизма, а решения (13) — угловые и линейные ускорения всех звеньев.

37

a := Diff_v(R,t,2)

substitute ,d φ (t)

ω

o

dt

O

substitute ,d φ (t)

ω

1

(t)

dt

1

substitute ,d φ (t)

ω

2

(t)

dt

2

substitute ,d φ (t)

ω

3

(t)

dt

3

substitute ,d Y(t)

V(t)

dt

a

0

→

substitute ,d V(t)

aD

dt

substitute ,d ω1(t)

ε1

dt

substitute ,d ω2(t)

ε2

dt

substitute ,d ω3(t) ε3 dt

substitute ,ω1(t) ω1 substitute ,ω2(t) ω2 substitute ,ω3(t) ω3 substitute ,φO(t) φO substitute ,φ1(t) φ1 substitute ,φ2(t) φ2 substitute ,φ3(t) φ3 simplify

2

d

− AB cos (φ1)ω1

2

2

+ O1B sin(φ2)ε2

−OA cos (φO) ωo

− OA sin(φO) dtωo

− AB sin(φ1)ε1 + O1B cos (φ2)ω2

−OA sin(φO) ωo2 + OA cos (φO) d ωo − AB sin(φ1)ω12 + AB cos

(φ1)ε1 + O1B sin(φ2)ω22

− O1B cos (φ2)ε2

dt

0

−O1C cos (φ2)

2

− O1C sin(φ2)ε2 − CD cos (

2

− CD sin(φ3)ε3

ω2

φ3)ω3

( 2)

2

2 + O1C cos

( 2)

ε

2

−

( 3)

3

( 3)

ε

3

− a

D

−O1C sin φ

ω

φ

CD sin φ

ω 2 +

CD cos φ

Рис. 2.1.7. Аналитические преобразования для нахождения ускорений.

38

Определение скоростей и ускорений узловых точек

Узловыми и задаваемыми точками многозвенного шарнирного механизма являются точки: A , B , C , D , M и K . Законы движения, угловые скорости и ускорения звеньев, а также закон движения, скорость и ускорение точки D определены ранее из уравнений (5) – (8), (11) и (13). Для остальных точек законы движения запишем в векторной форме.

Для определения скоростей и ускорений точек, учтем, что точки A , B и C принадлежат звеньям, совершающих вращательныедвижениявокруг неподвижных осей, а точки M и K — звеньям, совершающим плоское движение. В этом случае скорости точек A , B и C можно определить по формуле Эйлера, а скорости точек M и K согласнотеоремеосложениискоростейвплоскомдвижении.

При нахождении ускорений, воспользуемся формулой Ривальса для точек A , B и C , и теоремой о сложении ускорений в плоском движении твердого тела, для точек M и K .

Следует учесть, что векторы угловых скоростей и ускорений звеньев параллельны друг другу, и направлены перпендикулярно плоскости движения механизма.

2.1.2. ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ ПОСТАВЛЕННОЙ ЗАДАЧИ

При формировании документа Mathcad, реализующего поставленную выше задачу, использовались оба подхода для ее решения: явное задание функций, определяющих координаты звеньев механизма (аналитическое) и численное решение системы уравнений (3).

При решении задачи с помощью явного задания функций ϕ1 , ϕ2 , ϕ3 и yD ,

соотношения, вычисляющие искомые величины, представлены явными функциями времени, что означает привычную математическую запись выражений и прозрачный алгоритм. При численном решении поставленной задачи, каждая искомая величина вычисляется в виде вектора фиксированной длины, хранящегося в массиве данных и используемого по мере необходимости.

39

К недостаткам первого подхода, по сравнению со вторым, можно отнести большую длительность вычислений. Так, при построении графиков изменения основных кинематических характеристик с использованием 360 точек для каждой кривой, на PC с CPU Athlon XP1600 + и RAM 256 Мб, расчет занимает

57,8". В тоже время при численной реализации поставленной задачи, при про-

чих равных условиях, расчет занял 3,7".

Ниже представлен общий вид документа Mathcad, в котором производится кинематический расчет плоского механизма. В документе присутствуют скрытые зоны (Area). Внутри каждой расположены необходимые формулы для расчета. Все скрытые зоны имеют названия, соответствующие тем процедурам, по которым производится расчет кинематических характеристик механизма. К большинству процедур в документе даны необходимые пояснения. Содержимое скрытой зоны "Расчет механизма" приводится в двух редакциях: при аналитическом решении поставленной задачи (рис. 2.1.8) и при численном решении (рис. 2.1.11). Содержимое зоны "Формирование механизма и векторов" приведено на рис. 2.1.9, а "Результаты расчетов" на рис. 2.1.10 и рис. 2.1.12, соответственно для аналитического и численного решения.

Осуществление подключения документа "user_fun.mcd", в котором содержатся созданные ранее функции пользователя.

Reference:C:\Program Files\Mathsoft\user_fun.mcd

Чтение данных в матрицу "Ris" из файла под именем "Kin_01.bmp" для отображения схемы механизма

Ris := READBMP("Kin_01")	Ввод исходных данных
	a := 50					b := 37	OA := 15
	AB := 97					O1C := 45	O1B := 60
	CB := O1B − O1C
	CD := 86					AM := 42	CK := 47
	ωo :=		π			φo := 0
	18
	T :=	2 π				N := 360	:=	T
		ωo						N

Ris

40