Задача об оптимальном назначении до

ЗАДАЧА ОБ ОПТИМАЛЬНОМ НАЗНАЧЕНИИ

6.1. ПОСТАНОВКА ЗАДАЧИ

Пусть имеется n работ, которые могут выполнить n исполнителей. Известны затраты сi j , (i, j 1, 2,... n) при назначении i-го исполнителя на j- ую работу.

Требуется так распределить исполнителей по работам, чтобы все работы выполнялись, все исполнители были заняты и суммарные затраты при производстве работ были минимальны. Предполагается, что каждый исполнитель выполняет одну работу и каждая работа будет поручена одному исполнителю.

6.2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Обозначим назначение i-го исполнителя на j-ую работу, как xi j . Тогда

х11	х12	х13		...	х1n	1 ,
x21	x22	x23		...	x2n	1	,	(7.1)
xn 1	xn 2	x n	3	...	xn n	1 .

С другой стороны, каждая работа будет поручена одному исполнителю.

х11	х21	х31	...	хn1	1 ,
x12	x22	x3 2	...	xn2	1 ,	(7.2)
x1n	x2 n	x3n	...	xn n	1 , x i j 0, (i 1, 2,...n; j 1, 2,... n) .

Кроме того:

	xi j =	1, если i- тую работу выполняет исполнитель j;
		0, если i- тую работу не выполняет исполнитель j.

Функция цели задачи по критерию минимума суммарных затрат:

n n
f ( X )	Ci j xi j min .
i 1 j	1

Очевидно, что данная задача сводится к транспортной задаче, если запасы и потребности равны единице. Как правило, число исполнителей равно числу работ, то есть рассматривается закрытая задача. Если это условие не выполняется, то вводят либо фиктивного исполнителя, либо

фиктивную работу, в результате задача становится закрытой, а в полученном оптимальном назначении одна работа не будет выполнена, либо один исполнитель будет простаивать. Исходные данные задачи записываются в таблицу.

							Таблица 6.1
	B1	B2	B3	…	Bn		Запасы
А1	c11	c12	c13	…		c1n	1
	x11	x12	x13		x1n
А2	c21	c22	c23	…		c2n	1
	x21	x22	x23		x2n
…	…	…	…	…	…		…
Аn	cn1	cn2	cn3	…		cnn	1
	xn1	xn2	xn3		xnn
Потребности	1	1	1	1	1

Здесь А1 , А2 , …, Аn – работы, В1 , В2 , …, Вn – исполнители.

Так как «запасы» и «потребности» всегда равны 1, то при решении их не принято писать, кроме того величины «перевозок» также равны 1, поэтому занятые клетки можно просто отметить каким-либо образом.

Рассмотрим пример задачи о назначениях размерности n = 5. В табл. 6.2 приведен первый опорный план, построенный по методу северо-западного угла.

					Таблица 6.2
	В1	В2	В3	В4	В5
А1	12	8	14	10	24
	(1)
А2	31	15	22	7	30
		(1)
А3	20	25	21	26	26
			(1)
А4	11	17	18	15	8
				(1)
А5	6	5	9	9	19
					(1)

Из таблицы видно, что план вырожден n-1 раз. Такой особенностью обладают все планы задачи об оптимальном назначении. В результате стандартные методы решения транспортной задачи неэффективны и, кроме

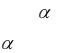
того, часто приводят к зацикливанию. Рассмотрим «венгерский метод» решения задачи.

6.3. РЕШЕНИЕ ЗАДАЧИ О НАЗНАЧЕНИЯХ ВЕНГЕРСКИМ МЕТОДОМ

Теорема Кенига. Если к стоимостям какой-либо строки (столбца) задачи о назначениях прибавить одно и тоже число, то оптимальный план не изменится.

АЛГОРИТМ РЕШЕНИЯ, ОСНОВАННЫЙ НА ТЕОРЕМЕ КЕНИГА:

1)выбрать в каждой строке минимальный элемент и вычесть его из всех элементов этой строки;

2)если в каком-нибудь столбце не появилось нулей, то из всех элементов такого столбца вычитается минимальный элемент этого же столбца;

3)рассматривается множество нулей таблицы и, если оно допустимо, то задача решена, иначе переходим к пункту 4;

4)минимальным числом прямых по строкам и столбцам вычеркиваются все нули, а из невычеркнутых элементов выбирается минимальный элемент ;

5) величина вычитается из невычеркнутых и прибавляется к дважды вычеркнутым элементам, после чего переходим к пункту 3.

Замечание. Допустимое множество нулей определяется следующим образом. Нулевой элемент в таблице с номером ij означает возможность выполнения i-тым исполнителем всей работы j. Поэтому расположение нужного количества нулей в таблице должно позволить выбрать единственным способом распределение всех работ между всеми исполнителями.

Сформулируем правило нахождения оптимального решения задачи о назначениях, в которой целевая функция минимизируется. Рассмотрим решение задачи на примере. Пусть задана матрица стоимости выполнения работ, причем для пяти работ имеется пять исполнителей.

1.Выберем в каждой строке матрицы наименьший элемент и вычтем его из каждого элемента этой строки.

2.Выберем столбцы, в которых нет нулей и найдем в них наименьший элемент. Затем вычтем его из каждого элемента столбца.

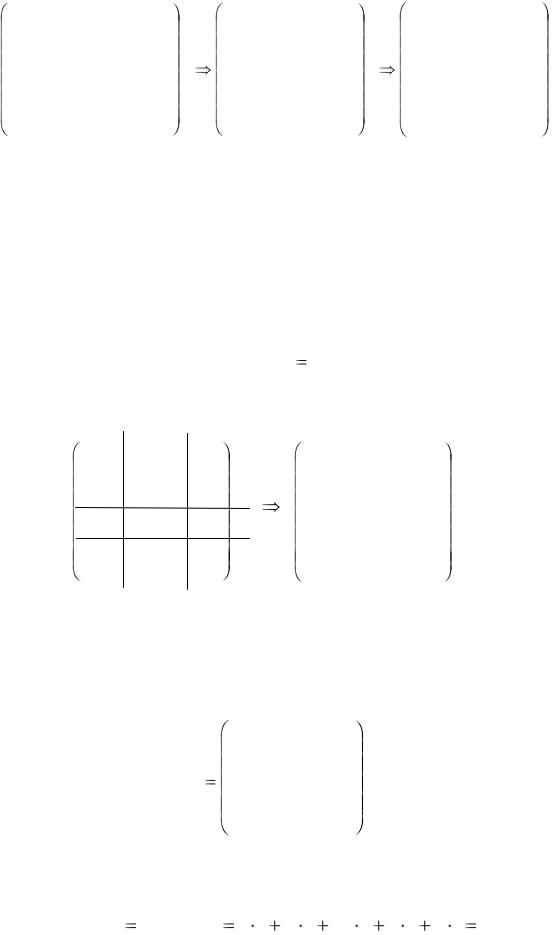
12	8	14	10	24	4	0	6			2	16	4			0	5	2	16
11	15	22	7	30	4	8	15			0	23	4			8	14	0	23
20	25	21	26	26	0	5	1			6	6	0			5	0	6	6 .
												3			9	9	7	0
11	17	18	15	8	3	9	10			7	0
6	5	9	9	19	1	0	4			4	14	1			0	3	4	14

3.Попробуем составить опорное решение из нулей, входящих в полученную матрицу. Но допустимого множества нулей не получено. В частности, выбрав один из нулей во втором столбце, например верхний

(работа А1 распределена второму исполнителю), мы не сможем использовать нижнюю строку с оставшимся нулем. Это означает, что работа А5 останется нераспределенной.

4.Вычеркиваем все нули, проведя наименьшее число прямых,

проходящих через все нули в матрице. Среди незачеркнутых найдем наименьший элемент, это элемент 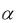1 (он дважды подчеркнут в

получившейся матрице), вычитаем его из всех невычеркнутых и прибавляем ко всем дважды вычеркнутым.

4			0	5	2	16	3	0			4			2		15
4			8	14	0	23	3	8			13			0		22
0			5	0	6	6
							0	6			0			7		6
3			9	9	7	0
							3	10			9			8		0
1			0	3	4	14
							0	0			2			4		13

5. Снова пытаемся составить опорное решение. Допустимое множество нулей получено (выделено двойным подчеркиванием). Из таблицы следует, что первый исполнитель выполняет работу 5, второй – работу 1 и т.д. Запишем решение в виде матрицы

	0	1	0	0	0
	0	0	0	1	0
X min	0	0	1	0	0
	1	0	0	0	0

Возвращаясь к исходной матрице, вычисляем минимальное значение функции цели

F(Х min ) F(X ) min 8 1 7 1 21 1 8 1 6 1 50 .

6.4. РЕШЕНИЕ ЗАДАЧИ МАКСИМИЗАЦИИ

Известно, что переход от задачи минимизации к задаче максимизации в линейном программировании достигается изменением знака функции цели.

F(X ) max F1 (X ) min , следовательно, данную задачу на нахождение максимума F ( X ) можно превратить в задачу минимизации, заменив знаки

всех элементов в матрице стоимостей. Далее решение находим методом, рассмотренным выше.

Пусть известен доход, который можно получить при назначении каждого исполнителя i (i = 1, 2,… n) на любую работу j ( j = 1, 2,… n). Найдем распределение исполнителей, которое принесет максимальную

прибыль.
Дана матрица
		12		8		14	10	24
		11		15		22	7	30
		20		25		21	26	26	,	меняя знаки, имеем:
		11		17		18	15	8
		6		5		9	9	19
						12	8		14		10		24
						11	15		22		7		30
						20	25		21		26		26
						11	17		18		15		8
						6	5		9		9		19
Прибавим к элементам всех строк модуль максимального элемента
этой же строки, а затем проделаем шаги 1 и 2.
		12		16		10	14	0			6	15	10	14	0
		19		15		8	23	0			13	14	8	23	0
		6		1		5	0	0			0	0	5	0	0	.
		7		1		0	3	10			1	0	0	3	10
		13		14		10	10	0			7	13	10	10	0
Множества допустимых нулей в матрице нет, следовательно,
продолжаем решение.
6	15	10	14			0		0	9	4	8	0		0	9	4	8	1
13	14	8	23			0		7	8	2	17	0		6	7	1	16	0
0	0	5		0		0		0	0	5	0	6		0	0	5	0	7
1	0	0		3	10			1	0	0	3	16		1	0	0	3	17
7	13	10	10			0		1	7	4	4	0		0	6	3	3	0

Получили оптимальное решение. Вычислим максимум функции цели, наложив эти нули на исходную матрицу.

0	8	3	7	1
6	6	0	15	0
1	0	5	0	8
2	0	0	3	18
0	5	2	2	0

F Xmax 12 22 26 17 19 96 ,

при этом первый исполнитель выполняет первую работу, второй – четвертую, третий вторую и т.д.