1.Свойства графически заданной функции

Рас­смот­рим функ­цию и «про­чтем» её гра­фик (см. рис. 1).

Рис. 1. Гра­фик функ­ции 

1. – про­ек­ция на ось;

2. – про­ек­ция на ось;

3. – корни (нули функ­ции);

4. ;

5. .

В целом функ­ция не мо­но­тон­на. Рас­смот­рим про­ме­жут­ки мо­но­тон­но­сти.

6.воз­рас­та­ет при, то есть боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет боль­шее зна­че­ние функ­ции (мо­но­тон­ность «в горку»);

7.убы­ва­ет при, то есть боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет мень­шее зна­че­ние функ­ции (мо­но­тон­ность «под горку»).

 Возрастающая функция

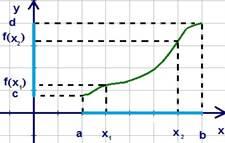
Рис. 2. Гра­фик воз­рас­та­ю­щей функ­ции

Опре­де­ле­ние. Функ­цию на­зы­ва­ют воз­рас­та­ю­щей на мно­же­стве, если для любыхииз мно­же­ства, таких, что, вы­пол­ня­ет­ся нера­вен­ство.

Разъ­яс­не­ние: боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет боль­шее зна­че­ние функ­ции (см. рис. 2).

 Убывающая функция

Опре­де­ле­ние. Функ­циюна­зы­ва­ют убы­ва­ю­щей на мно­же­стве, если для любыхмно­же­ства, таких, что, вы­пол­ня­ет­ся нера­вен­ство.

Разъ­яс­не­ние: боль­ше­му зна­че­нию ар­гу­мен­та со­от­вет­ству­ет мень­шее зна­че­ние функ­ции (см. рис. 3).

Рис. 3. Гра­фик убы­ва­ю­щей функ­ции

 Ограниченная снизу функция

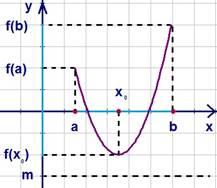
Рис. 4. Гра­фик огра­ни­чен­ной снизу функ­ции

Опре­де­ле­ние. Функ­циюна­зы­ва­ют огра­ни­чен­ной снизу на мно­же­стве, если все зна­че­ния функ­ции на мно­же­ствеболь­ше неко­то­ро­го числа (иными сло­ва­ми, если су­ще­ству­ет числотакое, что для лю­бо­го зна­че­ниявы­пол­ня­ет­ся нера­вен­ство) (см. рис. 4).

 Ограниченная сверху функция

Опре­де­ле­ние. Функ­циюна­зы­ва­ют огра­ни­чен­ной свер­ху на мно­же­стве, если все зна­че­ния функ­ции мень­ше неко­то­ро­го числа (иными сло­ва­ми, если су­ще­ству­ет числотакое, что для лю­бо­го зна­че­ниявы­пол­ня­ет­ся нера­вен­ство) (см. рис. 5).

Рис. 5. Гра­фик огра­ни­чен­ной свер­ху

 Наименьшее значение функции

Рис. 6. Гра­фик и наи­мень­шее зна­че­ние функ­ции

Опре­де­ле­ние. Число на­зы­ва­ют наи­мень­шим зна­че­ни­ем функ­циина мно­же­стве, если:

1. Всу­ще­ству­ет такая точка, что.

2. Для всехвы­пол­ня­ет­ся нера­вен­ство.

Ясно, что, если у функ­ции су­ще­ству­ет , то она огра­ни­че­на снизу (см. рис. 6).

 Наибольшее значение функции

Опре­де­ле­ние. Число на­зы­ва­ют наи­боль­шим зна­че­ни­ем функ­циина мно­же­стве, если:

1) всу­ще­ству­ет такая точка, что;

2) для всехвы­пол­ня­ет­ся нера­вен­ство.

Ясно, что, если у функ­ции су­ще­ству­ет , то она огра­ни­че­на свер­ху (см. рис.7).

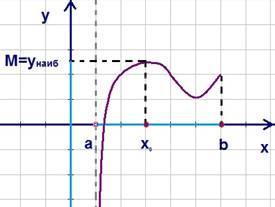
Рис. 7. Гра­фик и наи­боль­шее зна­че­ние функ­ции

 Понятие выпуклой функции

Функ­ция вы­пук­ла вниз на мно­же­стве (кри­вая под от­рез­ком) (см. рис.8).

Рис. 8. Гра­фик вы­пук­лой вниз функ­ции

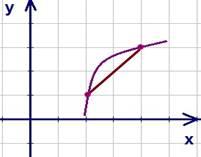
Рис. 9. Гра­фик вы­пук­лой вверх функ­ции

Функ­ция вы­пук­ла вверх на мно­же­стве(кри­вая над от­рез­ком) (см.рис. 9).

Понятие непрерывной функции

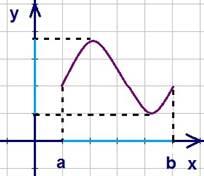
Рис. 10. Гра­фик непре­рыв­ной на от­рез­ке функ­ции

Непре­рыв­ность функ­ции на про­ме­жут­ке озна­ча­ет: гра­фик сплош­ной, без про­ко­лов и скач­ков (см. рис.10).

Рис. 11. Гра­фик функ­ции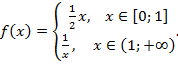 

При­мер функ­ции, ко­то­рая не яв­ля­ет­ся непре­рыв­ной (см. рис. 11):

.

.

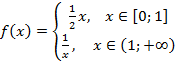 Пример:

По­стро­ить гра­фик функ­ции и «про­честь» его, ука­зать.

 

Ре­ше­ние. Гра­фик функ­ции на рис. 12.

Поясняю: корень квадратный не может быть отрицательным, т.е. у ≥ 0. Далее, преобразуем данное равенство (возведем в квадрат обе части), получим у² = 9 – х², перенесем слагаемые таким образом:

х² + у² =9 . Это уравнение окружности (х² + у² = r²) с центром в начале координат и радиусом равным 3.

 .

Поэтому график данной функции это часть окружности (помним об условии у ≥ 0).

Ответ: 1) ;

2) ;

3) воз­рас­та­ет при;

4) убы­ва­ет при;

5) .

 

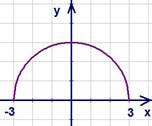Рис. 12. Гра­фик функ­ции