1894. Событие − вытащить наугад белый шар из выбранной наугад урны. Рассмотрим две гипотезы:− выбрать наугад первую урну,− вторую, причемВероятность вытащить белый шар из первой урны (условная вероятность), а вероятность событияпри условии, что событиепроизошлоИспользуя формулу полной вероятности (3.16), получим:

1895. 

1896. Известно, что из выбранной наугад урны вытащили белый шар, т. е. событие произошло. Необходимо найти вероятность гипотезы(была выбрана наугад первая урна) при условии, что событиепроизошло, т. е.Используя формулуБайеса (3.17), получим:

1897. 

1899. 3.2.12. Формула Бернулли. Наивероятнейшее число

1900. Наступлений события

1902. Схема Бернулли. Предположим, что производится n независимых испытаний, в результате каждого из них может наступить некоторое событие с одной и той же вероятностью или не наступить с вероятность

1903. Вероятность того, что событиепроизойдетm раз в n испытаниях, выражается формулой Бернулли:

1904. (3.18)

1905. где − число сочетаний изn элементов по m.

1906. Пример 3.34. Вероятность попадания в цель при одном выстреле равна 0,6. Какова вероятность того, что 5 выстрелов дадут 2 попадания?

1907. Используя формулу Бернулли (3.18) и учитывая, что иполучим:

1908. 

1909. Определение. Число называетсянаивероятнейшим числом наступлений события A в испытаниях, если не меньше остальных значенийт. е.при

1910. Если и, то значениеможно определить из двойного неравенства:

1911. (3.19)

1912. Разность граничных значений в неравенстве (3.19) равна единице. Если не является целым числом, то неравенство определяет лишь одно значение. Если жеявляется целым числом, то неравенство определяет дванаивероятнейших значения: и

1913. Пример 3.35. В урне 10 белых и 40 красных шаров. Вынимают наугад по одному 14 шаров, каждый раз возвращая вынутый шар в урну и тщательно перемешивая шары. Определить наивероятнейшее число появлений белого шара.

1914. Из условия задачи следует, что аИспользуя неравенство (3.19), получим:

1915. т. е.

1916. Таким образом, задача имеет два решения: и

1917. Пример 3.36. Вероятность попадания в цель при одном выстреле равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель.

1918. Из условия задачи следует, что аИспользуя неравенство (3.19), получим:

1919. т. е.

1920. Задача имеет одно решение:

1922. 3.2.13. Локальная формула Муавра−Лапласа

1924. В рамках схемы Бернулли при большом числе n независимых испытаний использовать формулу Бернулли нецелесообразно. В этих ситуациях используют локальную формулу Муавра−Лапласа.

1925. Локальная теорема Муавра−Лапласа. Вероятность того, что в n независимых испытаниях (чем больше n, тем точнее), в каждом из которых может наступить некоторое событие с одной и той же вероятностью или не наступить с вероятностьюсобытиенаступитm, приближенно равна:

1926. (3.20)

1927. где

1928. Функция является четной, следовательно,Таблица значений функциидля положительных значений аргументаприведена вприложении 1.

1929. Формулу (3.20) называют локальной формулой Муавра−Лапласа или локальной формулой Лапласа.

1930. Пример 3.37. Найти вероятность того, что событие наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.

1931. По условию задачи иТак как значениевелико, воспользуемся (3.20) локальной формулой Муавра−Лапласа:

1932. 

1933. В таблице значений функции (приложение 1) найдем и подставим в (3.20). Искомая вероятностьПример 3.38. Найти вероятность того, что событие наступит ровно 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.

1934. По условию задачи иТак как значениевелико, воспользуемся (3.20) локальной формулой Муавра−Лапласа:

1935. 

1936. Так как функция является четной, следовательно,В таблице значений функции(приложение 1) найдем и подставим в (3.20). Искомая вероятность

1938. 3.2.14. Интегральная формула Муавра−Лапласа

1940. Интегральная теорема Муавра−Лапласа. Вероятность того, что в n независимых испытаниях (чем больше n, тем точнее), в каждом из которых может наступить некоторое событие с одной и той же вероятностью или не наступить с вероятностьсобытиенаступит не менееи не болеераз, приближенно равна:

1941. (3.21)

1942. где − функция Лапласа.

1943. Функция является нечетной, следовательно,Таблица значений функциидля положительных значений аргументаприведена вприложении 2.

1944. Формулу (3.21) называют интегральной формулой Муавра−Лапласа или интегральной формулой Лапласа.

1945. Пример 3.39. Найти вероятность того, что событие наступит не менее 75 и не более 90 раз в 100 испытаниях, если вероятность появления этого события в каждом испытании равна 0,8.

1946. По условию задачи иТак как значениевелико, воспользуемся (3.21) интегральной формулой Муавра−Лапласа:

1947. 

1948. Учитывая нечетность функции т. е.найдем в таблице значений(приложение 2) и подставим в (3.21). В результате получим:

1949. 

1951. 3.2.15. Формула Пуассона

1953. Теорема Пуассона. При неограниченном увеличении числа n независимых испытаний в каждом из которых может наступить некоторое событие с одной и той же вероятностью стремящейся к нулюпри этомвероятность того, что событиенаступитm, приближенно равна:

1954. (3.22)

1955. Формулу (3.22) называют формулой Пуассона. Эта приближенная формула дает незначительные погрешности, если Значения функции Пуассонанаходят в таблице, приведенной вприложении 3, на пересечении соответствующих значений и

1956. Пример 3.40. Известно, что на 10000 выпущенных деталей приходится 10 бракованных. Какова вероятность того, что четыре случайно выбранные детали окажутся бракованными?

1957. По условию задачи Вероятность случайного выбора бракованной деталиТак как значениевелико, а− мало ивоспользуемся (3.22) и найдем значение функции Пуассона из таблицы (приложение 3) для значений и

1958. 

1960. Контрольные вопросы

1962. 1. Сформулировать определения понятий: случайного события, несовместных и независимых событий. Привести примеры.

1963. 2. Какое событие называется суммой и произведением событий?

1964. 3. В чем заключается статистический подход к понятию вероятности?

1965. 4. В чем заключается классический подход к понятию вероятности?

1966. 5. В чем заключается геометрический подход к понятию вероятности?

1967. 6. Сформулировать аксиоматическое определение понятия вероятности?

1968. 7. Чему равна вероятность суммы несовместных событий?

1969. 8. Чему равна вероятность произведения независимых событий?

1970. 9. Чему равна вероятность произведения зависимых событий?

1971. 10. Записать формулу полной вероятности и формулу Байеса. Привести примеры их применения для решения задач.

1972. 11. Записать формулу Бернулли. Привести примеры её применения для решения задач.

1973. 12. Записать локальную формулу Муавра−Лапласа. Привести примеры её применения для решения задач.

1974. 13. Записать интегральную формулу Муавра−Лапласа. Привести примеры её применения для решения задач.

1975. 14. Записать формулу Пуассона. Привести примеры её применения для решения задач.

1977. 3.3. Случайные величины

1979. При решении практических задач в различных областях (экономика, социология, политология, медицина и др.) с применением методов математической статистики широко используются понятия дискретных и непрерывных случайных величин, а также их основные характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение и т. д.

1981. 3.3.1. Дискретные случайные величины.

1982. Закон распределения дискретной случайной величины

1984. Под величиной обычно понимается характеристика объекта или процесса, которую можно измерить, т. е. сосчитать, например, при подсчете количества выпущенных деталей или сопоставить с эталоном, например, при измерении роста или веса человека.

1985. Определение. Дискретной случайной величиной называется переменная величина , принимающая в результате серии испытаний одно из значений…,, являющихся членами конечной или бесконечной числовой последовательности, с соответствующими вероятностями…,

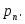
1986. Определение. Закон распределения дискретной случайной величины − функциональная зависимость вероятности от значений случайной величины

1987. Закон распределения дискретной случайной величины может быть задан, как и любая числовая функция, тремя способами:

• аналитически в виде уравнения

• графически (многоугольник распределения вероятностей);

• таблично.