8.5. Параметрические критерии различия

Критерии носят название ``параметрические'', потому, что в формулу их расчета включаются такие параметры выборки, как среднее, дисперсия и др. Как правило, в психологических исследованиях чаще всего применяются два параметрических критерия - это t - критерий Стьюдента, который оценивает различия средних для двух выборок и F - критерий Фишера, оценивающий различия между двумя дисперсиями.

.5.1. Т - Критерий Стьюдента

Критерий t Стьюдента направлен на оценку различий величин средних идвух выборок X и Y, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у связных и несвязных выборок, причем выборки могут быть не равны по величине.

Случай несвязных выборок

В общем случае формула для расчета по t - критерию Стьюдента такова:

где

Рассмотрим сначала равночисленные выборки. В этом случае n1 = n2 = n, тогда выражение (9.2) будет вычисляться следующим образом:

В случае неравночисленных выборок , выражение будет вычисляться следующим образом:

В обоих случаях подсчет числа степеней свободы осуществляется по формуле:

где n1 и n2 соответственно величины первой и второй выборки.

Понятно, что при численном равенстве выборок k = 2 n - 2.

Рассмотрим пример использования t - критерия Стьюдента для несвязных и неравных по численности выборок.

Пример: Психолог измерял время сложной сенсомоторной реакции выбора

(в мс) в контрольной и экспериментальной группах. В экспериментальную группу (X) входили 9 спортсменов высокой квалификации. Контрольной группой (Y) являлись 8 человек, активно не занимающихся спортом. Психолог проверяет гипотезу о том, что средняя скорость сложной сенсомоторной реакции выбора у спортсменов выше, чем эта же величина у людей, не занимающихся спортом.

Результаты эксперимента представим в виде табл. 9, в которой произведем ряд необходимых расчетов:

Таблица 9

№	Группы		Отклонение от среднего		Квадраты отклонения
	X	Y
1	504	580	- 22	- 58	484	3368
2	560	692	34	54	1156	2916
3	420	700	- 106	62	11236	3844
4	600	621	74	- 17	5476	289
5	580	640	54	- 2	2916	4
6	530	561	4	- 77	16	5929
7	490	680	- 36	42	1296	1764
8	580	630	54	- 8	2916	64
9	470	-	- 56	-	3136	-
Сумма	4734	5104	0	0	28632	18174
Среднее	526	638

Средние арифметические составляют в экспериментальной группе , в контрольной группе

Разница по абсолютной величине между средними

Подсчет выражения дает:

Тогда значение , вычисляемое по формуле (9.1), таково:

Число степеней свободы = 9 + 8-2= 15. По табл. 17 приложения 6 для данного числа степеней свободы находим:

2,13 для P 0,05

2,95 для P 0,01

4,07 для P 0,001

Строим ``ось значимости'':

Таким образом, обнаруженные психологом различия между экспериментальной и контрольной группами значимы более чем на 0,]% уровне, или, иначе говоря, средняя скорость сложной сенсомоторной реакции выбора в группе спортсменов существенно выше, чем в группе людей, активно не занимающихся спортом.

В терминах статистических гипотез это утверждение звучит так: гипотеза о сходстве отклоняется и на 0,1% уровне значимости принимается альтернативная гипотеза- о различии между экспериментальной и контрольными группами.

Случай связных выборок

В случае связных выборок с равным числом измерений в каждой можно использовать более простую формулу t - критерия Стьюдента.

Вычисления значений осуществляется по формуле:

где - разности между соответствующими значениями переменной X и переменной Y, асреднее этих разностей.

В свою очередь вычисляется по следующей формуле:

Число степеней свободы k определяется по формуле k = n - 1

Рассмотрим пример использования t - критерия Стьюдента для связных и, очевидно, равных по численности выборок.

Пример: Психолог предположил, что в результате научения время решения эквивалентных задач ``игры в 5'' (т. е. имеющих один и тот же алгоритм решения) будет значимо уменьшаться. Для проверки гипотезы у восьми испытуемых сравнивалось время решения (в минутах) первой и третьей задач. Решение задачи представим в виде табл. 10.

Таблица 10

№ испытуемых	1 задача	2 задача
1	4,0	3,0	1,0	1,0
2	3,5	3,0	0,5	0,25
3	4,1	3,8	0,3	0,09
4	5,5	2,1	3,4	11,56
5	4,6	4,9	-0,3	0,09
6	6,0	5,3	0,7	0,49
7	5,1	3,1	2,0	4,00
8	4,3	2,7	1,6	2,56
Суммы	37,1	27,9	9,2	20,04

Вначале произведем расчет по формуле:

Затем применим формулу:

И, наконец, следует применить формулу. Получим:

Число степеней свободы: k = 8 - 1 = 7 и по табл. 17 приложения 6 находим :

2,37 для P 0,05

З,50 для P 0,01

5,41 для P 0,001

Строим ``ось значимости'':

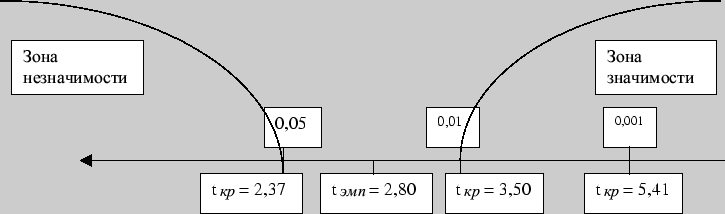
Таким образом, на 5% уровне значимости первоначальное предположение подтвердилось, действительно, среднее время решения третьей задачи существенно меньше среднего времени решения первой задачи. В терминах статистических гипотез полученный результат будет звучать так: на 5% уровне гипотеза отклоняется и принимается гипотеза-- о различиях.

Для применения t - критерия Стьюдента необходимо соблюдать следующие условия:

Измерение может быть проведено в шкале интервалов и отношений.

Сравниваемые выборки должны быть распределены по нормальному закону.