21. Системы однородных уравнений. Свойства решений, совместность.
Рассмотрим однородную систему
.
Однородная
система всегда совместна,
так как всегда имеет тривиальное
(нулевое) решение 
.
Выясним, когда данная система имеет
нетривиальное решение.
Теорема 1. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных.
Доказательство. Пусть система совместна. Это может быть тогда и только тогда, когда найдутся числа с1, с2, …, сn, при подстановке которых в систему мы получим m тождеств. Эти m тождеств можно записать в виде
.
Следовательно, система векторов-столбцов матрицы А линейно зависима. А это может быть тогда и только тогда, когда ранг системы векторов-столбцов меньше n, т.е. r(A)<n.
Следствие. Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель матрицы, составленной из коэффициентов при неизвестных, равен нулю.
Доказательство. Так как r(A)<n, то столбцы матрицы линейно зависимы и, следовательно, определитель матрицы равен нулю.
22. Системы однородных уравнений. Общее рещение систем.
Система
(1)
всегда имеет тривиальное решение. Если ранг матрицы, составленной из коэффициентов при неизвестных, меньше числа неизвестных, то система (1) имеет нетривиальные решения.
1) r(A)=n - система (1) имеет только тривиальное решение:
2) r(A)=r<n - система (1) имеет нетривиальные решения.
Количество свободных переменных во втором случае будет равно n-r, а базисных r. Давая свободным переменным произвольные значения, мы будем получать различные решения системы (1), т.е. любому вектору размерности n-r(сr+1, cr+2, …, cn)будет соответствовать решение системы (1)(с1, c2, …, cr, cr+1, …, cn).
Определение. Фундаментальной системой решений однородной системы (1) называется максимальная линейно независимая система решений системы (1). Фундаментальная система содержит n-r линейно независимых решений системы (1).
Чтобы
получить фундаментальную систему
решений, нужно в (n-r)-мерном
пространстве взять линейно независимую
систему из n-r векторов
и по ним построить соответствующие
решения системы (1). Полученные решения
будут образовывать фундаментальную
систему решений
.
Так как эта система максимальна, то
любое решение системы (1) можно представить
в виделинейной
комбинации решений
фундаментальной системы
.
Полученное выражение является общим
решением однородной системы (1)
23. Однородные системы линейных уравнений
дана однородная система
Рассмотрим соответствующую неоднородную систему
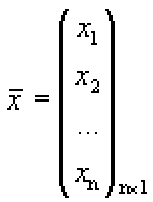
С
помощью матриц эти системы можно записать
в матричном виде.
Справедливы следующие свойства решений однородной и неоднородной систем.
Теорема 1. Линейная комбинация решений однородной системы (1) является решением системы (1).
Доказательство.
Пусть 
и
-
решения однородной системы.
Рассмотрим
,
где
-
некоторые произвольные числа. Так
как 
, и являются
решениями, то
, и . Найдем
.
является
решением системы (1).
Теорема 2. Разность двух решений неоднородной системы (2) является решением однородной системы (1).
Доказательство.
Пусть
и 
-
решения системы (2). Рассмотрим
..
является
решением однородной системы (1).
Теорема 3. Сумма решения однородной системы (1) с решением неоднородной системы (8.2) есть решение неоднородной системы (2).
Пусть
-
решение системы (1),
-
решение системы (2). Покажем, что
-
решение системы (2).
Доказательство. 
,
. является
решением неоднородной системы (2).