Виртуальная лабораторная работа №21

“ Определение логарифмического декремента и

Коэффициента затухания ”

Целью работы является изучение затухающих периодических колебаний и вычисление его математических параметров.

Введение. Рассмотрим затухающие колебания на примере горизонтальных колебаний твердого тела массы m , связанного со стенкой пружиной жесткостью k, масса которой m_пр << m (Рис.1). Трением между телом и полом будем пренебрегать ( к_тр =0). Сила сопротивления движению тела со стороны внешней среды F_c = -rV, где r –коэффициент сопротивления, а V – скорость тела. Будем решать задачу в случае движения тела вдоль оси Х.

Второй закон Ньютона в нашем случае при скорости тела V << c можно записать в виде

. (1)

В проекциях на оси Х и Y из (1) очевидно следуют уравнения:

→-kx – rV_x = m a_x , (2)

→N – mg = 0. (3)

Из (3) вытекает равенство N = mg. Из (2), поделив на m, с учетом, что

, окончательно получим дифференциальное уравнение в канонической форме

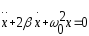, (4)

где 2β= r/m; ω₀²=k/m.

Будем искать решение уравнения (4) в виде («подстановка Эйлера»)

. (5)

Подставляя (5) в (4) получим

. (6)

Частными решениями квадратного уравнения (6) являются значения:

. (7)

Рассмотрим чаще всего встречающийся случай, когда затухание мало (<<). В этом случае решение (7)- числа комплексные:

, (8)

где 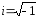(«мнимая единица»).

Общим решением уравнения (4) является линейная комбинация частных решений:

, (9)

где С₁ и С₂ комплексные коэффициенты, которые можно найти, принимая во внимание, что искомое x- принципиально вещественное число. То есть всегда должно выполняться равенство x = x^*, где x*- число, комплексно сопряженное числу x (Числом, комплексно сопряженным комплексному числу z = a + ib, называется комплексное число z = a – ib, где а и b- числа вещественные ).Поэтому можно написать:

. (10)

Подставляя в (10) значения λ₁ и λ₂ из (8), получим, что (10) верно, если выполняются соотношения:

. (11)

Из (11) следует, что

; . (12)

Подставляя (12) в (9), с учетом (8) и «формулы Эйлера»

, получим решение уравнения (4) в окончательном виде

(13)

где . (14)

График зависимости смещения от времени (2) показан на рис. 1 в виде зависимости х(t).

Рис.1

А₁, А₂, А₃ – амплитуды колебания, отличающиеся по времени равному периоду. Период затухающего гармонического колебания можно определить как:

(15)

Напомним, что периодом колебания называется время за которое совершается одно полное колебание.

Если рассматривать отношение амплитуд, отличающихся моментом времени равным периоду, то можно говорить еще об одной величине, характеризующей затухающее колебание, это декремент затухания:

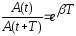(16)

Логарифм этого отношения называют логарифмическим декрементом затухания:

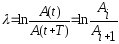(17)

где i = 1, 2, 3, … т.е. номер амплитуды.

Учитывая (16), для расчета величины λ получим

, (18)

где β – коэффициент затухания, T – период затухающего колебания, а для

для коэффициента затухания β формулу:

(19)

Уравнение, аналогичное (4), получается при рассмотрении электрических колебаний тока I в колебательном контуре, включающем последовательно соединенные конденсатор емкостью С, индуктивность L и сопротивление R:

,

где , а.

Очевидно, что в этом случае все выводы, сделанные при рассмотрении механических колебаний, правомочны и при описании затухающих колебаний тока в колебательном контуре.