12 Расчет нелинейной бортовой качки на нерегулярном волнении

Динамические свойства судна на нерегулярном волнении приближенно описываются дифференциальным уравнением следующего вида:

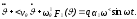₍₂₂₇₎

_{Нелинейность уравнения (227) не дает возможности применить для его решения спектральный метод, поэтому левую часть нужно предварительно линеаризировать. Для расчетов нелинейной бортовой качки наиболее удобен метод статистической линеаризации, согласно которому входящие в уравнение нелинейные члены заменяются линеаризированными зависимостями, эквивалентными исходным в вероятностном смысле. В соответствии с этим нелинейный член уравнения (227) аппроксимируется выражением:}

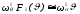(228)

В качестве условий эквивалентности левой и правой частей (228) можно принять следующие:

1. минимальная среднеквадратичная погрешность при аппроксимации;

2. равенства математических ожиданий и дисперсии исходной нелинейной функции и аппроксимирующей ее линейной;

3. энергостатистические равенства.

Воспользуемся вначале первым из перечисленных условий, которое приводит к весьма простым расчетным зависимостям.

Условие минимума среднеквадратической погрешности следующее:

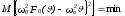, (229)

где М– символ математического ожидания.

Для реализации условия минимума приравняем нулю производную левой части равенства (229) по параметру

(230)

Возведем фигурную скобку в квадрат и учитывая, что математическое ожидание суммы равно сумме математических ожиданий слагаемых, получим:, (231)

, .

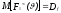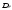–дисперсия относительных углов качки; D_f– дисперсия нелинейной функции .

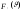Дифференцируя, найдем:

. (232)

Отсюда

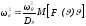. (233)

Это отношение определяет нормированную по дисперсии выходного процесса взаимокорреляционную функцию между входом и выходом процесса в нелинейной колебательной системе в одинаковые моменты времени.

Выразив математическое ожидание через плотность распределения вероятности угла качки f(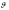), получим:

. (234)

Величина 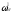является функцией дисперсии качки. Дисперсия качки– статистическая характеристика, определяющая интенсивность нерегулярных колебаний.

Если диаграмма статической остойчивости (функция ) задана графически или таблично, то величинаопределяется путем численного интегрирования по формуле (234).

Для получения достаточно простых аналитических зависимостей аппроксимируем диаграмму статической остойчивости параболой 5-ой степени [3]:

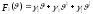, (235)

где– коэффициенты, определяемые в результате аппроксимации. Предположим, что углы качки распределены по нормальному закону:

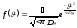(236)

Подставим (236) и (235) в (234):

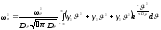(237)

Интегрируя полученное выражение, найдем:

, (238)

Перейдем, теперь ко второму критерию, который заключается в равенстве дисперсии исходной нелинейной функции и ей эквивалентной.

Дисперсия функции будет иметь вид:

. (239)

Ограничиваясь шестой степенью 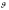, можно записать:

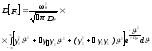. (240)

Учитывая, что 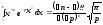будем иметь

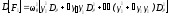. (241)

Дисперсия аппроксимирующей функции F₂=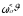 будет определяться формулой

. (242)

Приравнивая дисперси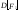и и, найдем

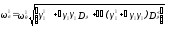(243)

Методов оценки погрешности, получаемой при использовании того или иного критерия, не существует, и поэтому выбор последнего по существу, произволен. Часто рекомендуется принимать в расчет полусумму результатов, получаемых по обоим критериям. Теперь можно реализовать аппроксимацию (228) и перейти от исходного нелинейного уравнения (227) к следующему:

₍₂₄₄₎

_{Для решения этого уравнения можно использовать спектральный метод, согласно которому спектральная плотность углов качки:}

,

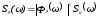где – спектральная плотность углов волнового склона;– передаточная функция качки.

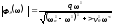. (245)

Отсюда спектральная плотность углов качки

. (246)

Зная её, можно найти дисперсию углов качки

. (247)

Так как входящая в правую часть величина 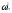зависит от дисперсии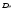, то для определения последней необходимо решать систему уравнений (234) ,(243)и (247). Это можно осуществить численными методами. Вычислив дисперсию можно найти статистические амплитуды качки. Так амплитуда 3%-й обеспеченности:

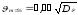, (248)

а средняя амплитуда

. (249)

В случае квадратичного закона сопротивления можно использовать результаты Г.А. Фирсова и коэффициент демпфирования заменить следующим образом :

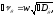(250)

где

.
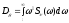